Static Hedging and Pricing American Exotic Options SanLin

Static Hedging and Pricing American Exotic Options San-Lin Chung, Pai-Ta Shih*, and Wei-Che Tsai Presenter: Pai-Ta Shih National Taiwan University 1

Outlines p p p The main contributions Introduction Formulation of the static hedging portfolio The hedge performance of static versus dynamic hedging of an American up-and-out put option Efficiency of the static hedge portfolio for pricing American exotic options Conclusions 2

The main contributions 1. We show to construct static hedge portfolios for American barrier options and floating strike lookback options due to the complexity of boundary conditions of the option. 2. We investigate the hedging performance of the proposed method and compare with that of the dynamic hedge strategy. 3. This article proposes an efficient numerical method for pricing American barrier options and floating strike lookback options. 3

Introduction o Pricing and hedging American-style exotic options is an important yet difficult problem in the finance literature. n Lattice methods: Boyle and Lau (1994), Ritchken (1995), Cheuk and Vorst (1996), and Chung and Shih (2007) n Analytical approximation formulae: Gao, Huang, and Subrahmanyam (2000), Ait. Sahlia, Imhof, and Lai (2003), and Chang, Kim, and Kim (2007) 4

Introduction o Extend the seminal works of Derman, Ergener, and Kani (1995) and Carr, Ellis, and Gupta (1998) to several ways: 1. Beyond the Black-Scholes model: o Andersen, Andreasen, and Eliezer (2002), Fink (2003), Nalholm and Poulsen (2006 a), and Takahashi and Yamazaki (2009) 2. Several replication methods: o the risk-minimizing method of Siven and Poulsen (2009) o the line segments method of Liu (2010) 5

Introduction 3. Beyond the barrier options: o American options (Chung and Shih (2009)) o European Asian options (Albrecher, Dhaene, Goovaerts, and Schoutens (2005)) o European Installment options (Davis, Schachermayer, and Tompkins (2001)) 6

Introduction o This paper utilizes the static hedge portfolio (SHP) approach to price and/or hedge American exotic options. o At least three advantages: 1. The proposed method is applicable for more general stochastic processes, but the existing numerical or analytical approximation methods may be difficult to extend them to other stochastic processes, e. g. the constant elasticity of variance (CEV) model of Cox (1975). 7

Introduction 2. The hedge ratios, such as delta and theta, are automatically derived at the same time when the static hedge portfolio is formed. 3. When the stock price and/or time to maturity instantaneously change, the recalculation of the prices and hedge ratios for the American exotic options under the proposed method is quicker than the initial computational time because there is no need to solve the static hedge portfolio again. 8

Formulation of the static hedging portfolio p We demonstrate how to construct the SHP for an American up-andout put option and the SHP for an American floating strike lookback put option under the Black-Scholes model. 9

The static hedge portfolio for an American up-and-out put 10

The static hedge portfolio for an American up-and-out put o Our static hedge portfolio starts with one unit of the corresponding European option to match the terminal condition of the AUOP. p At time t(n-1), three conditions imply that 11

The static hedge portfolio for an American up-and-out put Figure 1. The static hedge portfolio for an AUOP option 12

The static hedge portfolio for an American up-and-out put o Using similar procedures, we work backward to determine the number of units of the European option. o Finally, the value of the n-point static hedge portfolio at time 0 is obtained as follows: 13

The static hedge portfolio for an American floating strike lookback put o We use the underlying asset as the numeraire and express the price of an American floating strike lookback put option. 14

The hedge performance of static versus dynamic hedging of an American up-and-out put option o According to CBOE’s equity option product specifications, the strike price interval is $2. 5 when the strike price is between $5 and $25, $5 when the strike price is between $25 and $200, and $10 when the strike price is over $200. We consider two types of SHPs. n The first SHP is formed by exactly following the previous procedure and we call this portfolio is termed “SHP with nonstandard strikes”. n The second portfolio utilizes European put options with standard 15 strikes and thus is called “SHP with standard strikes”.

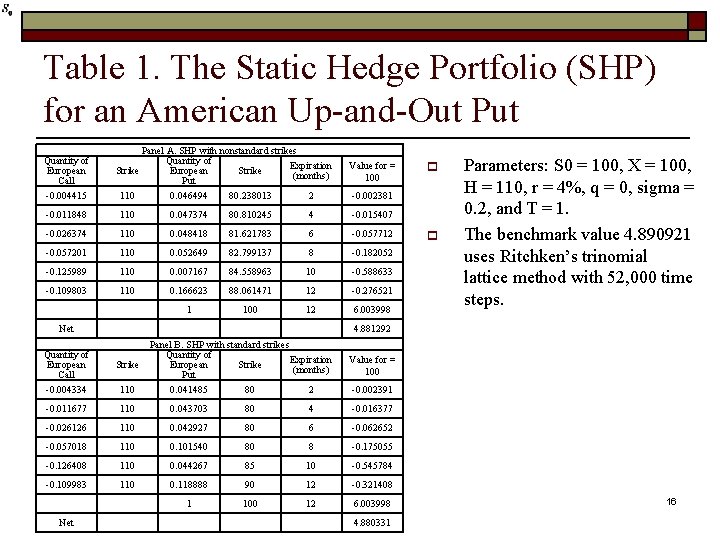
Table 1. The Static Hedge Portfolio (SHP) for an American Up-and-Out Put Quantity of European Call Panel A. SHP with nonstandard strikes Quantity of Expiration Strike European Strike (months) Put Value for = 100 -0. 004415 110 0. 046494 80. 238013 2 -0. 002381 -0. 011848 110 0. 047374 80. 810245 4 -0. 015407 -0. 026374 110 0. 048418 81. 621783 6 -0. 057712 -0. 057201 110 0. 052649 82. 799137 8 -0. 182052 -0. 125989 110 0. 007167 84. 558963 10 -0. 588633 -0. 109803 110 0. 166623 88. 061471 12 -0. 276521 1 100 12 6. 003998 Net Quantity of European Call p Parameters: S 0 = 100, X = 100, H = 110, r = 4%, q = 0, sigma = 0. 2, and T = 1. The benchmark value 4. 890921 uses Ritchken’s trinomial lattice method with 52, 000 time steps. 4. 881292 Panel B. SHP with standard strikes Quantity of Expiration Strike European Strike (months) Put Value for = 100 -0. 004334 110 0. 041485 80 2 -0. 002391 -0. 011677 110 0. 043703 80 4 -0. 016377 -0. 026126 110 0. 042927 80 6 -0. 062652 -0. 057018 110 0. 101540 80 8 -0. 175055 -0. 126408 110 0. 044267 85 10 -0. 545784 -0. 109983 110 0. 118888 90 12 -0. 321408 1 100 12 6. 003998 Net p 4. 880331 16

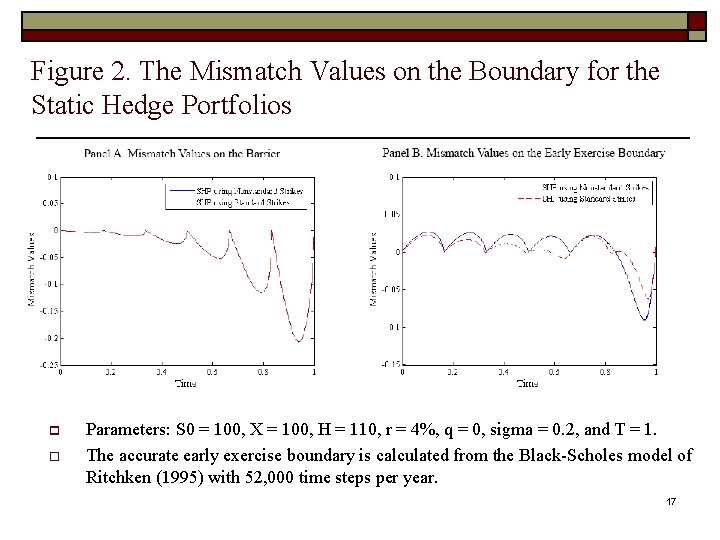
Figure 2. The Mismatch Values on the Boundary for the Static Hedge Portfolios p o Parameters: S 0 = 100, X = 100, H = 110, r = 4%, q = 0, sigma = 0. 2, and T = 1. The accurate early exercise boundary is calculated from the Black-Scholes model of Ritchken (1995) with 52, 000 time steps per year. 17

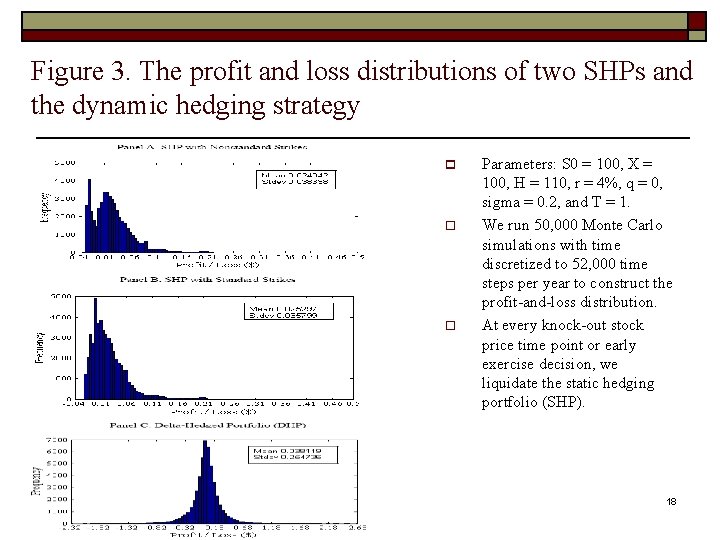
Figure 3. The profit and loss distributions of two SHPs and the dynamic hedging strategy p o o Parameters: S 0 = 100, X = 100, H = 110, r = 4%, q = 0, sigma = 0. 2, and T = 1. We run 50, 000 Monte Carlo simulations with time discretized to 52, 000 time steps per year to construct the profit-and-loss distribution. At every knock-out stock price time point or early exercise decision, we liquidate the static hedging portfolio (SHP). 18

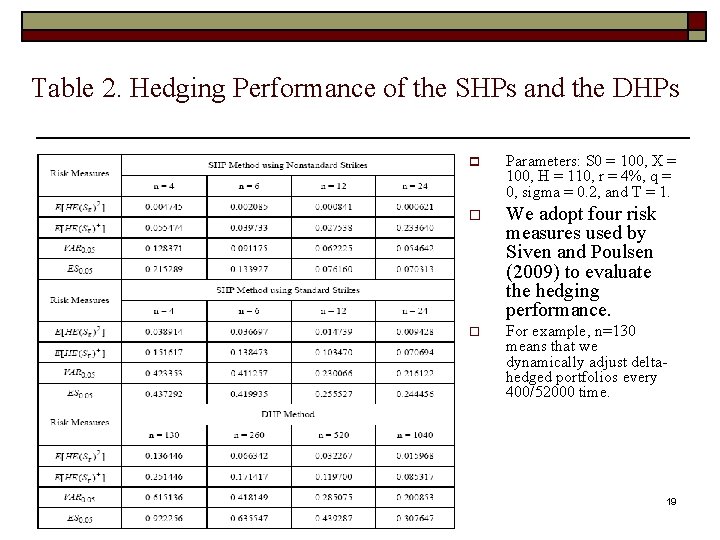
Table 2. Hedging Performance of the SHPs and the DHPs p Parameters: S 0 = 100, X = 100, H = 110, r = 4%, q = 0, sigma = 0. 2, and T = 1. o We adopt four risk measures used by Siven and Poulsen (2009) to evaluate the hedging performance. o For example, n=130 means that we dynamically adjust deltahedged portfolios every 400/52000 time. 19

Efficiency of the static hedge portfolio for pricing American exotic options o In this section, we will evaluate the numerical efficiency of the SHP approach for pricing American barrier options and American lookback options, respectively. n n In the former case, we consider pricing AUOP options under the CEV model of Cox (1975). In the latter case, we consider valuing American floating strike lookback put options under the BS model to demonstrate that the proposed method is applicable for other types of exotic options beyond barrier options. 20

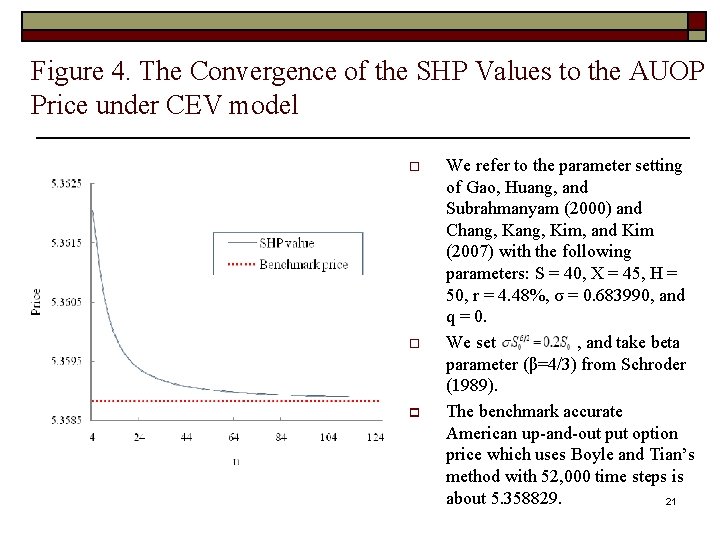
Figure 4. The Convergence of the SHP Values to the AUOP Price under CEV model o o p We refer to the parameter setting of Gao, Huang, and Subrahmanyam (2000) and Chang, Kim, and Kim (2007) with the following parameters: S = 40, X = 45, H = 50, r = 4. 48%, σ = 0. 683990, and q = 0. We set , and take beta parameter (β=4/3) from Schroder (1989). The benchmark accurate American up-and-out put option price which uses Boyle and Tian’s method with 52, 000 time steps is about 5. 358829. 21

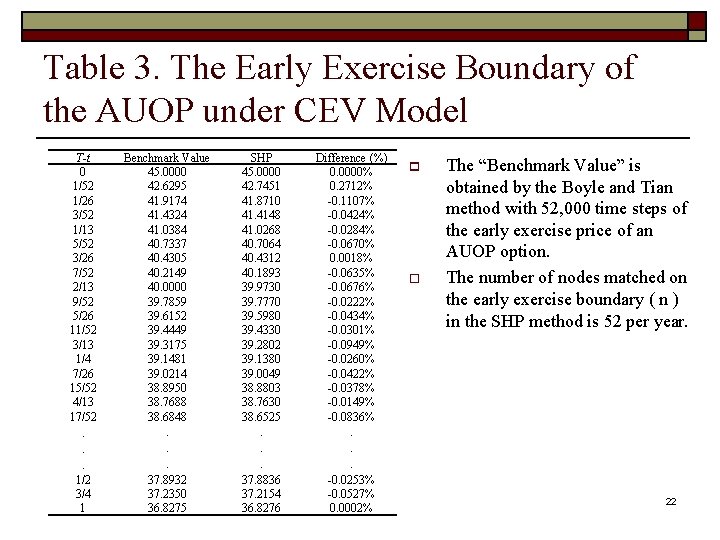
Table 3. The Early Exercise Boundary of the AUOP under CEV Model T-t 0 1/52 1/26 3/52 1/13 5/52 3/26 7/52 2/13 9/52 5/26 11/52 3/13 1/4 7/26 15/52 4/13 17/52. . . 1/2 3/4 1 Benchmark Value 45. 0000 42. 6295 41. 9174 41. 4324 41. 0384 40. 7337 40. 4305 40. 2149 40. 0000 39. 7859 39. 6152 39. 4449 39. 3175 39. 1481 39. 0214 38. 8950 38. 7688 38. 6848. . . 37. 8932 37. 2350 36. 8275 SHP 45. 0000 42. 7451 41. 8710 41. 4148 41. 0268 40. 7064 40. 4312 40. 1893 39. 9730 39. 7770 39. 5980 39. 4330 39. 2802 39. 1380 39. 0049 38. 8803 38. 7630 38. 6525. . . 37. 8836 37. 2154 36. 8276 Difference (%) 0. 0000% 0. 2712% -0. 1107% -0. 0424% -0. 0284% -0. 0670% 0. 0018% -0. 0635% -0. 0676% -0. 0222% -0. 0434% -0. 0301% -0. 0949% -0. 0260% -0. 0422% -0. 0378% -0. 0149% -0. 0836%. . . -0. 0253% -0. 0527% 0. 0002% p o The “Benchmark Value” is obtained by the Boyle and Tian method with 52, 000 time steps of the early exercise price of an AUOP option. The number of nodes matched on the early exercise boundary ( n ) in the SHP method is 52 per year. 22

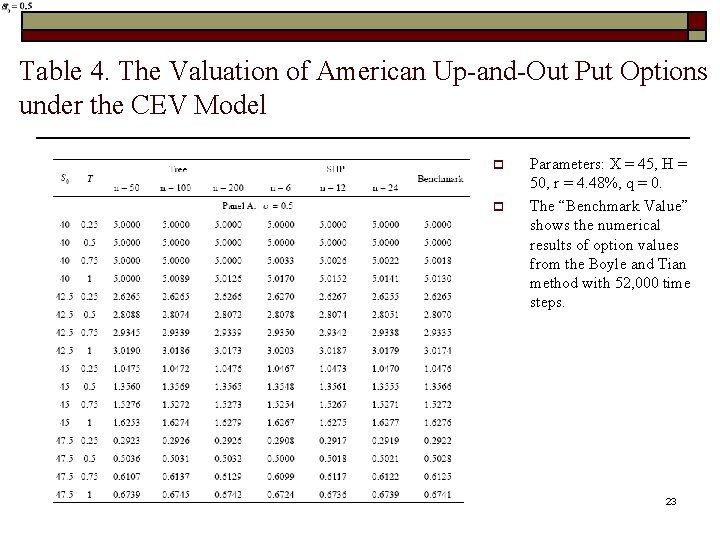
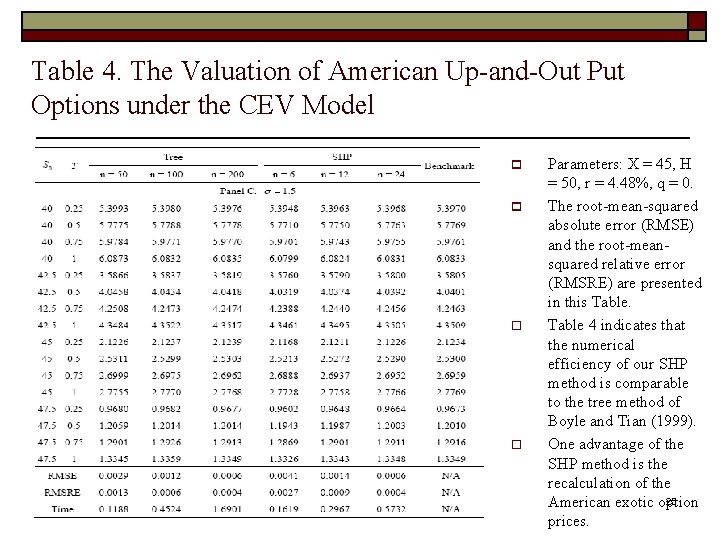
Table 4. The Valuation of American Up-and-Out Put Options under the CEV Model p p Parameters: X = 45, H = 50, r = 4. 48%, q = 0. The “Benchmark Value” shows the numerical results of option values from the Boyle and Tian method with 52, 000 time steps. 23

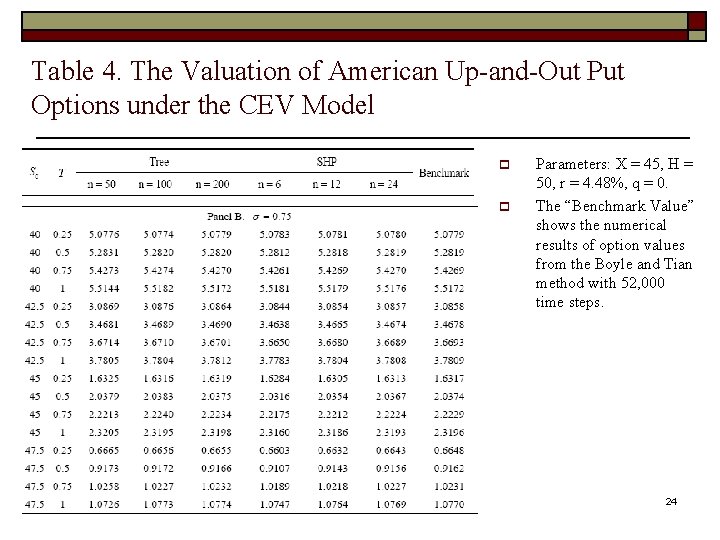
Table 4. The Valuation of American Up-and-Out Put Options under the CEV Model p p Parameters: X = 45, H = 50, r = 4. 48%, q = 0. The “Benchmark Value” shows the numerical results of option values from the Boyle and Tian method with 52, 000 time steps. 24

Table 4. The Valuation of American Up-and-Out Put Options under the CEV Model p p o o Parameters: X = 45, H = 50, r = 4. 48%, q = 0. The root-mean-squared absolute error (RMSE) and the root-meansquared relative error (RMSRE) are presented in this Table 4 indicates that the numerical efficiency of our SHP method is comparable to the tree method of Boyle and Tian (1999). One advantage of the SHP method is the recalculation of the 25 American exotic option prices.

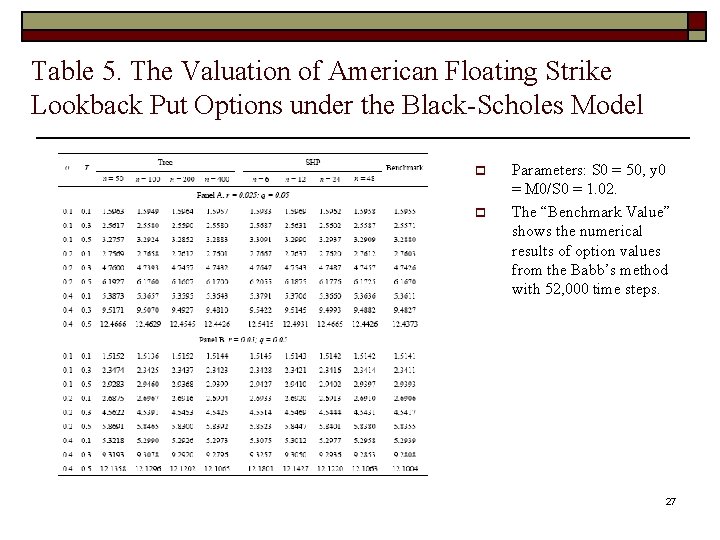
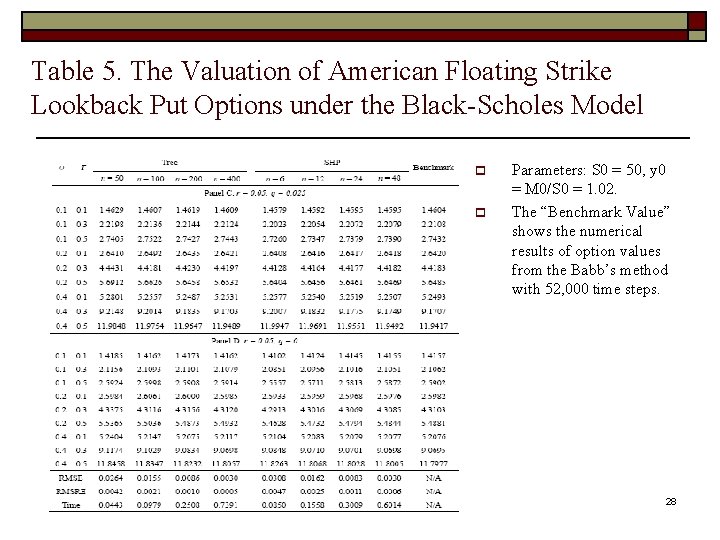
Pricing American floating strike lookback put options under the Black-Scholes model o The numerical results are based on the parameter setting of Chang, Kim, and Kim (2007) and are reported in Figure 5 and Table 5. p p Parameters: S 0 = 50, y 0 = M 0/S 0 = 1. 02. The “Benchmark Value” shows the numerical results of option values from the Babb’s method with 52, 000 time steps. 26

Table 5. The Valuation of American Floating Strike Lookback Put Options under the Black-Scholes Model p p Parameters: S 0 = 50, y 0 = M 0/S 0 = 1. 02. The “Benchmark Value” shows the numerical results of option values from the Babb’s method with 52, 000 time steps. 27

Table 5. The Valuation of American Floating Strike Lookback Put Options under the Black-Scholes Model p p Parameters: S 0 = 50, y 0 = M 0/S 0 = 1. 02. The “Benchmark Value” shows the numerical results of option values from the Babb’s method with 52, 000 time steps. 28

Conclusions o We successfully construct a static hedge portfolio to match the terminal and boundary conditions of American barrier options and lookback options. o We show that while the average profit and loss values of all hedge portfolios are similar, the SHPs are far less risky than the DHPs no matter which risk measure is used. o We conduct detailed efficiency analyses and show that the proposed method is as efficient as the numerical methods for pricing American barrier options under the CEV model and American lookback options under the Black-Scholes model. 29