Static Electricity Electric Forces Electric Fields Static Electricity

Static Electricity, Electric Forces, Electric Fields

Static Electricity • Static Electricity involves charges “at rest”. • Fundamental Rule of Charge – Opposite charges attract – Like charges repel • 3 methods of charging : friction, conduction, & induction • Conductors allow electrons to move freely, Insulators do not!

Methods of Charging • Charging by friction – two neutral objects are rubbed together and become oppositely charged ( the object that gains electrons becomes negatively charged and the one that loses electrons becomes positively charged) • Charging by induction – a charged object is brought near but not touching a neutral object ( the neutral object gets a temporary charge separation – gets opposite charge near the charged object) • Charging by conduction – a charged object touches a neutral object so charges are transferred between objects until they reach charge equilibrium, ie. have equal charge (the neutral object gets the same charge)

Electric Forces Given 2 charges of magnitude q 1 & q 2 separated by a distance d, the magnitude of the force that each of the charges exerts on the other is calculated using Coulomb’s Law. The forces can be attractive or repulsive and must be equal and opposite … Newton’s 3 rd Law! Coulomb’s Law: F q 1 q 2 + F - F d + + q 1 q 2 F FE = electrostatic force, Newtons (N) k = electric or Coulomb’s constant = 9 x 109 Nm 2/C 2 q 1 = charge of the first object, C q 2 = charge of the second object, C d = distance between the two charges (center to center), m

Electric Charges • Electrons have a negative charge • Protons have a positive charge • Charge is measured in “coulombs” • “qo” or “Q” in an equation is used for charge • 1 electron has -1. 6 x 10 -19 C of charge

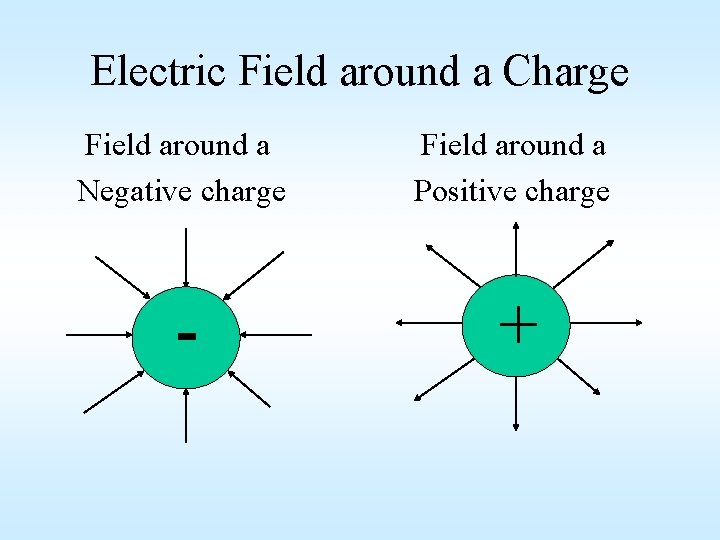
Electric Fields • Electric fields are the “energy fields” that surrounds any charged particle” • Any charge placed in this field will experience a force. • Electric fields are vectors (magnitude & direction). • The direction of an electric field is defined by the direction of the force on a tiny “+” test charge placed in that field. Thus electric fields are always in a direction that is away from “+” and toward “-”. • Electric Field strength is the force per unit charge and is measured in units of N/C (Newtons per Coulomb) E = Electric Field Strength, N/C F = Electrostatic Force, N qo = Charge placed in the electric field, C

Electric Field around a Charge Field around a Negative charge Field around a Positive charge - +

Note - In the formulas on the previous slide and on the following slides q 0 and Q are described as follows: Q = charge of the object causing the electric field, C qo = test charge or the charge of the object placed in the field, C

Electric Field Strength at a point near a charge Q + . E d E= electric field strength, N/C k = electric or Coulomb’s constant (9 x 109) Q = charge causing the field, C d = distance from the charge to where the field strength is being measured, m

Electric Potential Difference • Electric Potential Difference is the potential energy per unit charge at a given point due to an electric field. • Units: Volts (1 volt = 1 Joule per Coulomb) • Potential Difference is required to make current flow. ΔV = Electric Potential Difference, Volts ΔPE =change in electric potential energy, J qo= charge placed in an electric field, C Note: 1 Volt = 1 Joule / Coulomb

Potential Difference at a Point ΔVP = Potential Difference at a point, V k = Coulomb’s constant = 9 x 109 Nm 2/C 2 Q d . Q = Charge causing the electric field, C VP d = distance between Q and where VP is being measured, m

Electric Potential Energy between 2 charges q 1 d q 2

Work done on a charge So: • W- the work required to move a charge through a potential difference, Joules (J) • - magnitude of the charge placed in the field, Coulombs (C) • V - potential difference, Volts (V)

Electric Potential of a charge moving in a uniform electric field ∆V = electric potential difference, V E = electric field strength, V/m or N/C d = displacement moved along the field lines, m Note: It must be a uniform electric field! Also there is no ∆PE and thus no ∆V if displacement is perpendicular to the electric field.

Capacitor – a device used to store charge. Example of a common simple capacitor: 2 oppositely charged plates + - • increase the size of the plates + - • decrease the plate separation + - • increase the voltage of the battery + - battery E To get more stored charge: + - Note: This is an example of a uniform electric field. Insulator such as air

Capacitance – the ability of a conductor to store energy in the form of electrically separated charges C = Capacitance, Farads (F) Q = charge on one plate, C ∆V = Potential difference, V Note: 1 Farad = 1 Coulomb / Volt Also, a Farad is a very large unit so usually use μF or p. F. (micro = μ = 10 -6, nano = n = 10 -9, pico = p = 10 -12)

Electrostatics Formulas Note: The top two and next two equations look alike except for d 2 vs d. The ones on the left are vector quantities and have d 2 while the ones on the right have d and are not vectors.