Static Analysis of Communication Structures in Parallel Programs

Static Analysis of Communication Structures in Parallel Programs So-Yan Ho and Nai-Wei Lin Department of Computer Science and Information Engineering National Chung Cheng University

Motivations • Communication structures in message passing programs is the key to understand the behaviors of the programs • Static analysis of communication structures allows programmers to identify potential communication bugs at compile time 2

Message Passing Schemes • Direct-Addressing: CSP, Occam, Ada, MPI send(task-id, message); message = receive(task-id); • Indirect-Addressing: Fortran M, CCC send(channel-id, message); message = receive(channel-id); 3

Channels in CCC • Pipes: one-to-one communication • Spliters: one-to-many communication • Mergers: many-to-one communication • Multiplexers: many-to-many communication 4

Merits of Abundant Channels • Communication structures are more comprehensive • The specification of communication structures is easier • The implementation of communication structures is more efficient • The static analysis of communication structures is more effective 5

Higher-Order Channels • A channel is first-order if it is used to transfer data • A channel is higher-order if it is used to transfer channels • The static analysis of higher-order channels is much more difficult than the static analysis of first-order channels 6

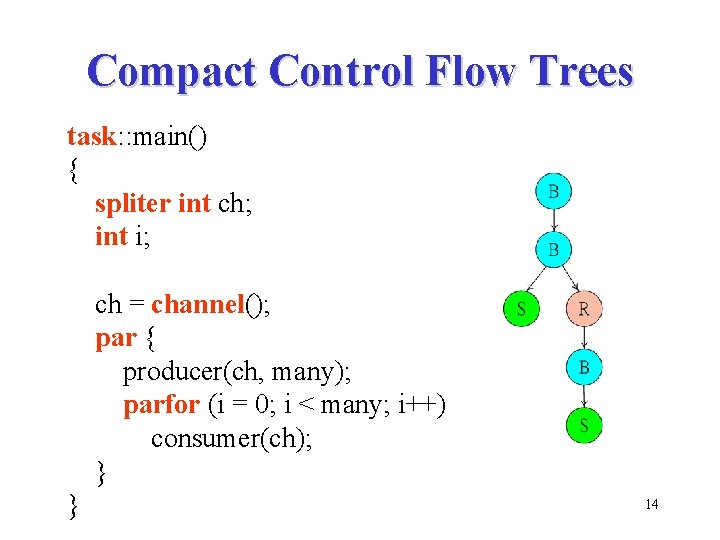
A Simple CCC Program task: : main() { spliter int ch; int i; /* one-to-many channel */ ch = channel(); par { producer(ch, many); /* one sender */ parfor (i = 0; i < many; i++) consumer(ch); /* many receivers */ } } 7

A Simple CCC Program task: : producer(ch, many) spliter int ch; int many; { int i; for (i = 0; i < num_data; i++) send(ch, i); for (i = 0; i < many; i++) send(ch, end_data); /* signal end of data */ } 8

A Simple CCC Program task: : consumer(ch) spliter int ch; { int data; while (1) { data = receive(ch); if (data == end_data) break; process(data); } } 9

Overview of the Analysis • For each channel ch, infer the number of senders of ch, ch. s and the number of receivers of ch, ch. r • Intraprocedural analysis: within a function – infer them once and for all, and use them as the initial values of the interprocedural analysis • Interprocedural analysis: among functions – propagate the values among functions until they reach a fixed point 10

First-Order Channels • Use aliasing induced by parameter passing • For each channel ch, infer ch. s = ch. self. s + ch. others. s ch. r = ch. self. r + ch. others. r where, ch. self. s, ch. self. r: {0, 1} ch. others. s, ch. others. r: {0, 1, 2} • We call the four tuple {ch. self. s, ch. self. r, ch. others. s, ch. others. r} the mode of ch 11

Intraprocedural Analysis • For each channel ch, if ch is sent by current function then ch. self. s = 1 else ch. self. s = 0 if ch is received by current function then ch. self. r = 1 else ch. self. r = 0 12

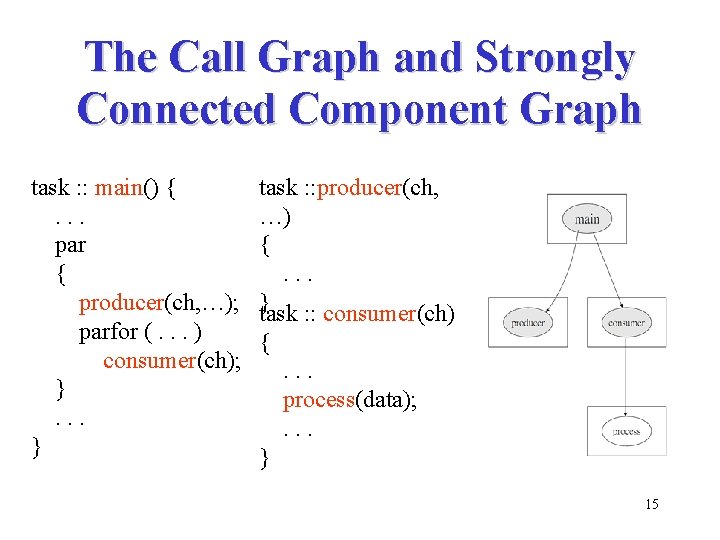
Interprocedural Analysis • Compact control flow trees – call nodes, spawn nodes, block nodes, alternative nodes, repetition nodes – depth-first order (once) • The call graph and the strongly connected component graph – topological sort order (once) • Strongly connected components – worklist (iterations) 13

Compact Control Flow Trees task: : main() { spliter int ch; int i; ch = channel(); par { producer(ch, many); parfor (i = 0; i < many; i++) consumer(ch); } } 14

The Call Graph and Strongly Connected Component Graph task : : main() {. . . par { producer(ch, …); parfor (. . . ) consumer(ch); }. . . } task : : producer(ch, …) {. . . }task : : consumer(ch) {. . . process(data); . . . } 15

Call Nodes • Let L be the set of channel parameters aliased with ch at the call node n • Then chn. self. s = x L x. self. s, chn. self. r = x L x. self. r, chn. others. s = x L x. others. s, chn. others. r = x L x. others. r 16

Spawn Nodes • Let L be the set of channel parameters aliased with ch at the spawn node n • Then chn. self. s = 0, chn. self. r = 0, chn. others. s = x L x. self. s + x L x. others. s, chn. others. r = x L x. self. r + x L x. others. r 17

Block Nodes • If the block node n is the initial node chn. self. s = value from intraprocedural analysis, chn. self. r = value from intraprocedural analysis, chn. others. s = 0, chn. others. r = 0 • Otherwise chn. self. s = 0, chn. self. r = 0, chn. others. s = 0, chn. others. r = 0 18

Bolck Nodes • Let L be the sequence of nodes inside the block node n • Then chn. self. s = chn. self. s || x L chx. self. s, chn. self. r = chn. self. r || x L chx. self. r, chn. others. s = chn. others. s + x L chx. others. s, chn. others. r = chn. other. r + x L chx. others. r 19

Alternative Nodes • Let L be the sequence of nodes inside the alternative node n • Then chn. self. s = maxx L chx. self. s, chn. self. r = maxx L chx. self. r, chn. others. s = maxx L chx. others. s, chn. others. r = maxx L chx. others. r 20

Repetition Nodes • Let m be the node inside the repetition node n • Then chn. self. s = chm. self. s, chn. self. r = chm. self. r, chn. others. s = if chm. others. s == 0 then 0 else 2, chn. others. r = if chm. others. r == 0 then 0 else 2 21

Second-Order Channels • Use aliasing induced by both parameter passing and message passing • For each second-order channel ch, infer ch. s. S = the set of channels sent to ch ch. r. S = the set of channels received from ch 22

Intraprocedural Analysis • For each second-order channel ch, ch. s. S = ch. r. S = For each first-order channel x, if x is sent to ch ch. s. S = ch. s. S ∪ { x } if x is received from ch ch. r. S = ch. r. S ∪ { x } 23

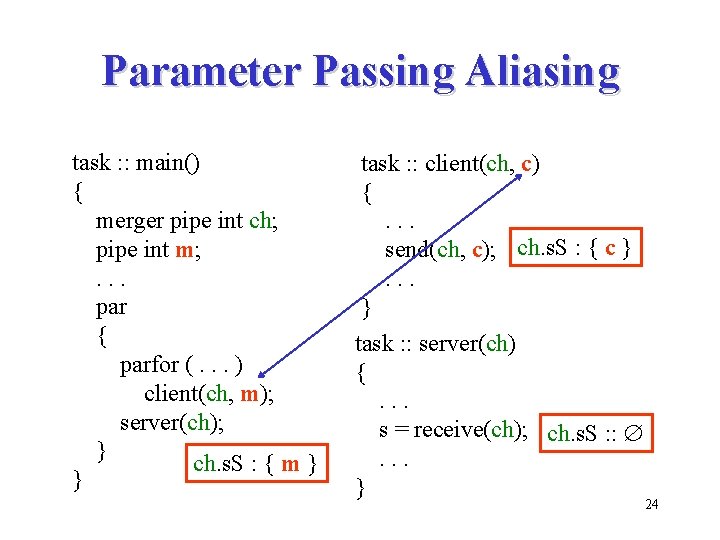
Parameter Passing Aliasing task : : main() { merger pipe int ch; pipe int m; . . . par { parfor (. . . ) client(ch, m); server(ch); } ch. s. S : { m } } task : : client(ch, c) {. . . send(ch, c); ch. s. S : { c }. . . } task : : server(ch) {. . . s = receive(ch); ch. s. S : : . . . } 24

Call and Spawn Nodes • Let S be the set of second-order channel parameters aliased with ch at the call node n • Let F be the set of first-order channel parameters at n, and for each p F, let (p) represent the corresponding channel argument of p at n • Then chn. s. S = x S x. s. S{ p F , p/ (p)} , chn. r. S = x S x. r. S { p F , p/ (p)} 25

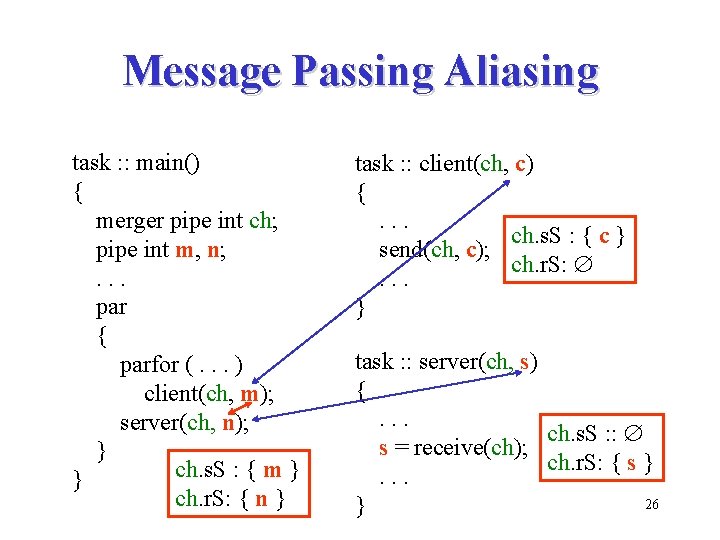
Message Passing Aliasing task : : main() { merger pipe int ch; pipe int m, n; . . . par { parfor (. . . ) client(ch, m); server(ch, n); } ch. s. S : { m } } ch. r. S: { n } task : : client(ch, c) {. . . ch. s. S : { c } send(ch, c); ch. r. S: . . . } task : : server(ch, s) {. . . ch. s. S : : s = receive(ch); ch. r. S: { s }. . . 26 }

Call and Spawn Nodes • For each x in ch. s. S, x is aliased with every y in ch. r. S • Then, for each c in {x} ch. r. S c. self. s = d {x} ch. r. S d. self. s, c. self. r = d {x} ch. r. S d. self. r, c. others. s = d {x} ch. r. S d. others. s, c. others. r = d {x} ch. r. S d. others. r 27

Block Nodes • If the block node n is the initial node chn. s. S = value from intraprocedural analysis, chn. r. S = value from intraprocedural analysis • Otherwise chn. s. S = , chn. r. S = 28

Block Nodes • Let L be the sequence of nodes inside the block node n • Then chn. s. S = chn. s. S x L chx. s. S, chn. r. S = chn. r. S x L chx. r. S 29

Alternative Nodes • Let L be the sequence of nodes inside the alternative node n • Then chn. s. S = x L chx. s. S, chn. r. S = x L chx. r. S 30

Repetition Nodes • Let m be the node inside the repetition node n • Then chn. s. S = chm. s. S, chn. r. S = chm. r. S 31

Time Complexity intraprocedural analysis; for each SCC in SCCG begin while changed begin for each CCFT in the SCC begin for each node in the CCFT begin … endfor endwhile endfor The time complexity: O(V+E) 32

Conclusions • Design a linear algorithm to infer the number of senders and receivers for each channel • Handle both first-order and higher-order channels • Use the information about aliasing induced by both parameter passing and message passing 33