Static analysis for security Luis Sierra November 2007

Static analysis for security Luis Sierra November, 2007 Stic Am. Sud - Re. Se. Co Workshop Montevideo, Uruguay

Plan • • • Some motivation Static analysis Py. STA: Python Static Analyzer Permission usage analysis Conclusions and further work

Motivation • To understand have experience of the permissions model of Besson, Dufay, and Jensen • Looking for a quick prototype • Moreover, I did not know Python
![[x : = 2]1; [y : = 4]2; [x : = 1]3; [read (z)]4; [x : = 2]1; [y : = 4]2; [x : = 1]3; [read (z)]4;](http://slidetodoc.com/presentation_image_h2/75f16fe5af87ac7eae767a705df69d7e/image-4.jpg)
[x : = 2]1; [y : = 4]2; [x : = 1]3; [read (z)]4; if [z > x]5 then [z : = y]6 else [z : = x]7 Static analysis: example • Take a program S • Take a property P Every assignment is useful • Check if P holds in every possible execution of S – Checking at compile time – Approximate answers
![[x : = 2]1; [y : = 4]2; [x : = 1]3; [read (z)]4; [x : = 2]1; [y : = 4]2; [x : = 1]3; [read (z)]4;](http://slidetodoc.com/presentation_image_h2/75f16fe5af87ac7eae767a705df69d7e/image-5.jpg)
[x : = 2]1; [y : = 4]2; [x : = 1]3; [read (z)]4; if [z > x]5 then [z : = y]6 else [z : = x]7 Static analysis: example Every assignment is useful • Check if P holds in every possible execution Pysta of S – Checking at compile time • 1 : set([]) • 2 : set(['y']) • 3 : . . .
![[x : = 2]1; [y : = 4]2; [x : = 1]3; [read (z)]4; [x : = 2]1; [y : = 4]2; [x : = 1]3; [read (z)]4;](http://slidetodoc.com/presentation_image_h2/75f16fe5af87ac7eae767a705df69d7e/image-6.jpg)
[x : = 2]1; [y : = 4]2; [x : = 1]3; [read (z)]4; if [z > x]5 then Om; [z : = y]6 else [z : = x]7 Static analysis: example • Take a program S • Take a property P Every assignment is useful • If Om does not terminate, we should delete assignment 2. Our analysis solves the halting problem !!! – Checking at compile time – Approximate answers
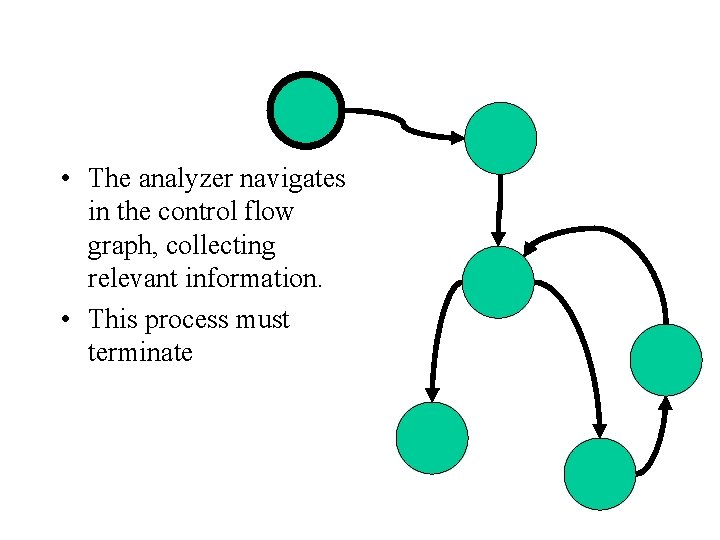
• The analyzer navigates in the control flow graph, collecting relevant information. • This process must terminate

Working list • The analyzer navigates in the CFG with an iterator • We exploit Python flexibility defining – an implementation with sets – and an implementation with lists

Working list class working. List (object): def iter (self): pass def add (self, c): pass def MFP (a): W = WLmap [WLoption] (a. flow) for (l 1, l 2) in W. iter (): . . . W. add ([(s, t) for (s, t) in. . . ]). . .
![Fix-point computation def MFP (a): W = WLmap [WLoption] (a. flow) for (l 1, Fix-point computation def MFP (a): W = WLmap [WLoption] (a. flow) for (l 1,](http://slidetodoc.com/presentation_image_h2/75f16fe5af87ac7eae767a705df69d7e/image-10.jpg)
Fix-point computation def MFP (a): W = WLmap [WLoption] (a. flow) for (l 1, l 2) in W. iter (): fl = a. transfer (l 1) if (not a. latt. leq (fl, a. a [l 2])): a. a [l 2] = a. latt. join (a. a [l 2], fl) W. add ([(s, t) for (s, t) in a. flow if s==l 2]) a. dump ()

A static analysis • The analysis is declared in the main program def analyze (file, analysis. Type): s = open (file + '. xml'). read() p = parse. String (s). document. Element a = analysis. Type (p) MFP (a)

Some implementations • As well as with working lists, we implemented several static analysis – Live variables – Constraint propagation – Available expressions – Permission usage

A class for analysis class MF (object): def __init__ (self, pgm, an): . . . def. Lattice (self): pass defextremal. Value (self): pass def transfer (self, l, s): pass def initial. Analysis (self): self. a = {} for l in self. Lab: self. a [l] = self. extremal. Value if l in self. extremal. Label else self. latt. bottom (). . .

Live Variables Analysis class Analysis (MF): def __init__ (self, pgm): MF. __init__ (self, pgm, 'BW') def. Lattice (self): self. latt = Set. Var. Lat () defextremal. Value (self): self. extremal. Value = Set. Var ([]) def transfer (self, l): . . . def kill (self, l): return Set. Var (eval (get. Kill (self. Blocks[l]))) def gen (self, l): return Set. Var (eval (get. Gen (self. Blocks[l])))

Lattices • The information collected in a static analysis is good enough to provide – an operation of least upper bound (latt. join) – a comparison (latt. leq) • We are not interested in proving that a structure is a lattice, but in implementing quickly the relevant operations

A lattice class lattice (object): def U (self): """Support set of the lattice. Meaningful if the support set is finite. """ pass def join (self, a, b): """Join operation: returns a new object with value in the lattice. """ pass def leq (self, a, b): """Less or equal relation: returns True or False. """ pass def bottom (self): """Bottom: returns a new object """ pass

A library of lattices class semilattice (object): . . . ## a cartesian product using tuples class cartesian. Product (lattice): . . . ## a function space class functionspace (lattice): . . . ## a function using a dictionary class gen. Function (object): . . . class newbottom (lattice): . . . class powerset (lattice): . . . class dual (lattice):

Multiplicities and permissions 1 0

Permissions lattice

Permissions analysis class Analysis (MF): . . . def. Lattice (self): self. latt = Perm (self. Resources, self. Action, self. Res. Type) defextremal. Value (self): self. extremal. Value = self. latt. bottom () def transfer (self, l): . . . class Perm (functionspace): . . .

Permissions analysis class Res (powerset): . . . class Act (powerset): . . . class Perm. RT (newbottom): . . . class Mult (lattice): . . . class Perm. Mult (cartesian. Product): . . . class RTfunc (one. Function): . . . class Perm (functionspace): . . .

A program grant (http ('*'), read, inf) grant (https ('site'), read, 1) grant (file ('wallet. Id'), read, 1) while. . . : consume (http ('site'), read) if. . . : consume (http ('*'), read) else: break consume (file ('wallet. Id'), read) if. . . : consume (http ('site'), read) else: grant (file ('wallet. Visa'), read, 1) consume (file ('wallet. Visa'), read) consume (https ('site'), read)
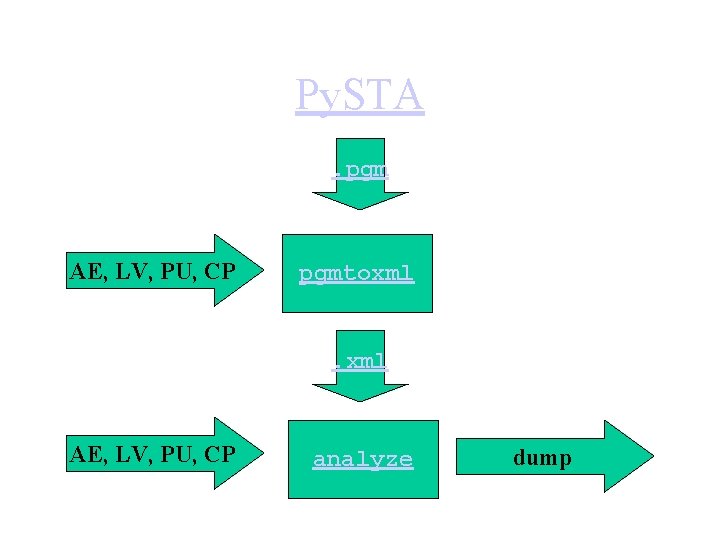
Py. STA. pgm AE, LV, PU, CP pgmtoxml AE, LV, PU, CP analyze dump
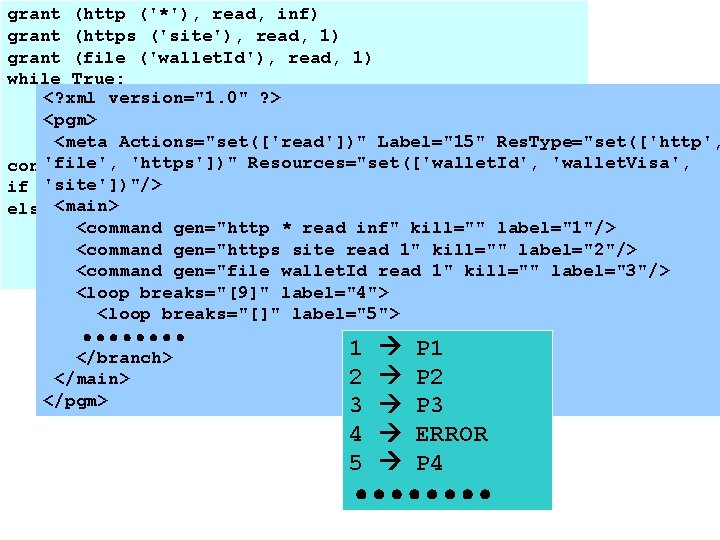
grant (http ('*'), read, inf) grant (https ('site'), read, 1) grant (file ('wallet. Id'), read, 1) while True: <? xml while version="1. 0" True: consume ? > (http ('site'), read) <pgm> if True: consume (http ('*'), read) <meta break Actions="set(['read'])" Label="15" Res. Type="set(['http', else: 'file', 'https'])" Resources="set(['wallet. Id', 'wallet. Visa', consume (file ('wallet. Id'), read) 'site'])"/> if True: consume (http ('site'), read) else: <main> <command * read, inf" kill="" label="1"/> grant (file gen="http ('wallet. Visa'), 1) <command gen="https site read 1" kill="" label="2"/> consume (file ('wallet. Visa'), read) <command gen="file wallet. Id consume (https ('site'), read) read 1" kill="" label="3"/> <loop breaks="[9]" label="4"> <loop breaks="[]" label="5"> 1 P 1 </branch> 2 P 2 </main> </pgm> 3 P 3 4 ERROR 5 P 4

Conclusions and further work • Python is a good tool for fast and modular programming • Compare the classes of Py. STA with the Coq viewpoint • Program interesting examples • Modify the permissions model using ad hoc constructs • Program new analyses

Bibliography • A Formal Model of Access Control for Mobile Interactive Devices. Frédéric Besson, Guillaume Dufay, and Thomas Jensen
- Slides: 26