States Of Matter And Behavior Of Gases Honors

States Of Matter And Behavior Of Gases Honors Chemistry – Chapter 13 -14

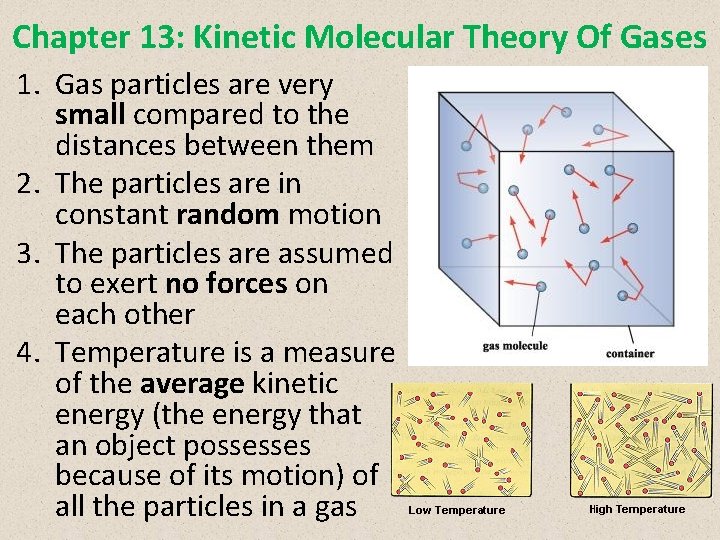
Chapter 13: Kinetic Molecular Theory Of Gases 1. Gas particles are very small compared to the distances between them 2. The particles are in constant random motion 3. The particles are assumed to exert no forces on each other 4. Temperature is a measure of the average kinetic energy (the energy that an object possesses because of its motion) of all the particles in a gas

Kinetic Molecular Theory Of Gases • Approximates true nature of gases • Like most models, it has limits of usefulness • Correctly predicts behavior of many gases Solid Liquid Gas

Measuring Temperature • Chemist use both the Celsius ( C) scale and the Kelvin (K) scale: • The Celsius scale is based on the temperatures at which water freezes (0 C) and boils (100 C) • Kelvin scale is based absolute zero (0 K): theoretical C + 273 = K temperature at which all K 273 = C particle motion stops. -223 C + 273 = 50 K Therefore, there are no 50 K 273 = -223 C negative Kelvin values!

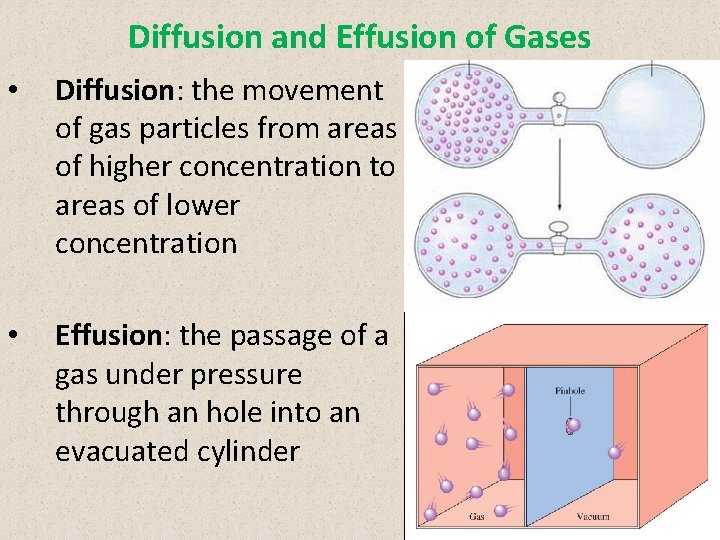
Diffusion and Effusion of Gases • Diffusion: the movement of gas particles from areas of higher concentration to areas of lower concentration • Effusion: the passage of a gas under pressure through an hole into an evacuated cylinder

Pressure = Force/Area; measured in Pascals (SI unit) • For a gas, pressure is the result of particles colliding with the sides of the container • Atmospheric pressure measured with a barometer • Converting pressure units: 1 atmosphere (atm) = 101, 325 Pascals (Pa) = 101. 325 k. Pa = 760 torr = 760 mm Hg = 14. 7 psi

Law of Partial Pressures • The total pressure of a gas mixture is the sum of the pressure each gas exerts if it were alone in the same volume • The partial pressure of each gas in a mixture of gases in a container depends on the number of moles of that gas Mathematically: Ptotal = P 1 + P 2 + … + Pn Ptotal = total pressure P 1, P 2, etc. = partial pressure of each gas in the mixture

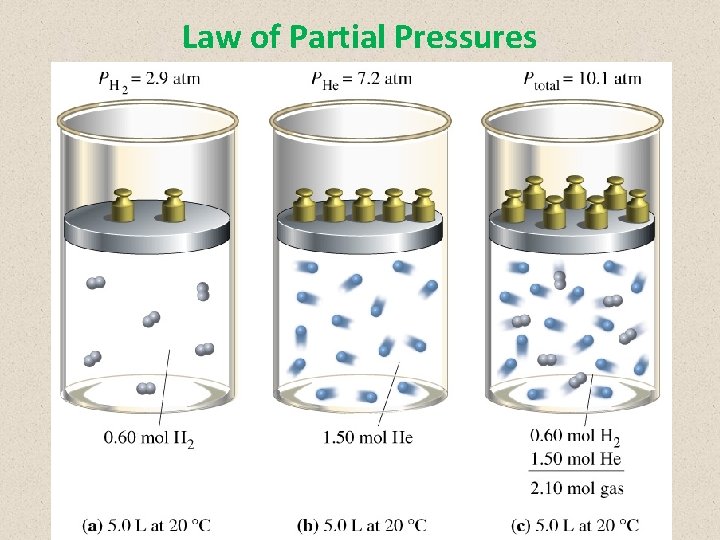
Law of Partial Pressures

Example Law of Partial Pressures Problem Air is made of four main gases: N 2, O 2, Ar, and CO 2. Air pressure at sea level = 760 mm Hg. What is the partial pressure of oxygen if the partial pressures of the other gases in air are (in mm Hg): N 2 = 594, Ar = 7. 10, and CO 2 = 0. 23? Ptotal = PN 2 + PO 2 + PAr + PCO 2 Ptotal - PN 2 - PAr - PCO 2 = PO 2 760 - 594 - 7. 10 - 0. 23 = PO 2 158. 67 mm Hg = PO 2

Phase Changes In order for a substance to change its phase (state) of matter, the temperature and/or the pressure of the substance must change. • Boiling Point: temperature and pressure at which a substance changes from a liquid to a gas • Melting Point: temperature and pressure at which a substance changes from a solid to a liquid • Sublimation Point: temperature and pressure at which a substance changes from a solid to a gas

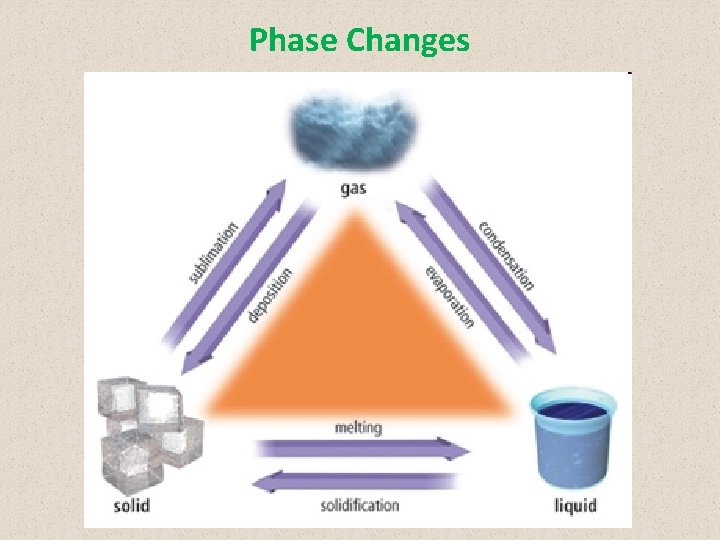
Phase Changes

Phase Changes • • • All phase changes can be classified as exothermic or endothermic. Exothermic Phase Changes: release energy (heat) Condensation – gas to liquid Releasing energy makes particles Freezing – liquid to solid move more slowly Deposition – gas to solid Endothermic Phase Changes: absorb energy (heat) Melting – solid to liquid Absorbing energy Vaporization – liquid to gas makes particles Sublimation – solid to gas move more quickly

Vaporization • All liquids have a vapor pressure: the pressure of a gas over a liquid. It increases as temperature increases. • Vaporization/boiling occurs when the vapor pressure equals the atmospheric pressure. • Vaporization/boiling is different from evaporation: the escape of water vapor at a liquid’s surface

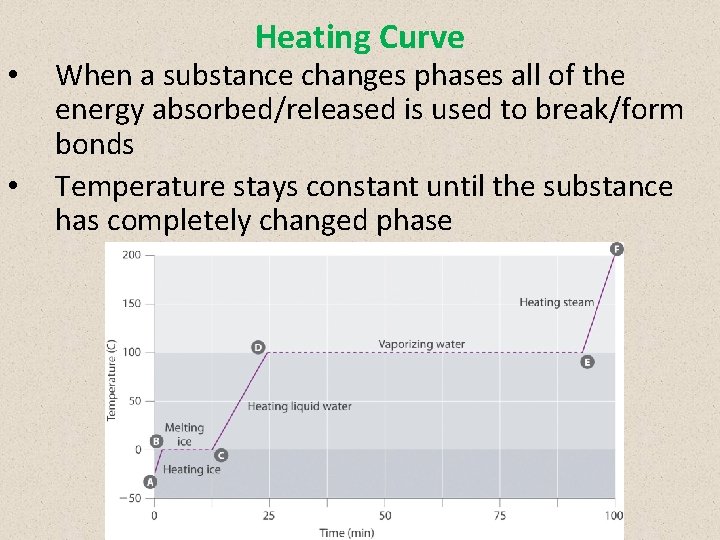
• • Heating Curve When a substance changes phases all of the energy absorbed/released is used to break/form bonds Temperature stays constant until the substance has completely changed phase

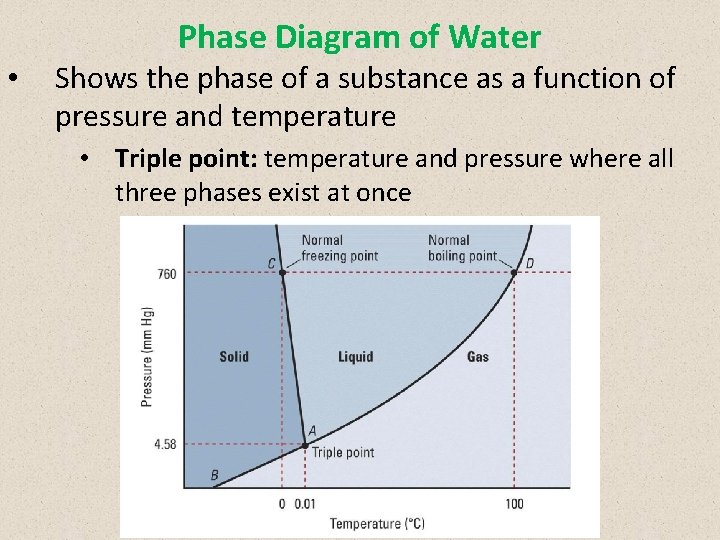
Phase Diagram of Water • Shows the phase of a substance as a function of pressure and temperature • Triple point: temperature and pressure where all three phases exist at once

Phase Diagram of Carbon Dioxide

Chapter 14: Gas Laws • Ideal gas: a gas that perfectly follows that assumptions of the Kinetic Molecular Theory and thus perfectly follows the gas laws • In reality, no such gas exists, but hydrogen and helium act most like ideal gases, especially at high temperatures and low pressures

Boyle’s Law • States that the volume of a gas is inversely proportional to the pressure of a gas at constant temperature: P 1 V 1 = P 2 V 2 • If volume increases, pressure decreases and if volume decreases, pressure increases

Boyle’s Law Example Problem • A sample of He gas is compressed from 4. 0 L into 2. 5 L at constant temperature. If the pressure of the gas is 210 k. Pa at 4. 0 L what will be the pressure at 2. 5 L? P 1 V 1 = P 2 V 2 (210 k. Pa)(4. 0 L) = P 2(2. 5 L) (2. 5 L) (210 k. Pa)(4. 0 L) = P 2 (2. 5 L) 336 k. Pa = P 2

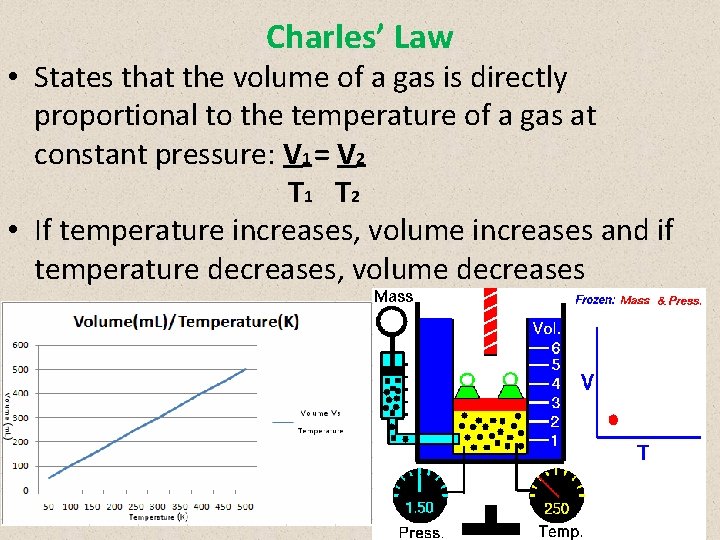
Charles’ Law • States that the volume of a gas is directly proportional to the temperature of a gas at constant pressure: V 1 = V 2 T 1 T 2 • If temperature increases, volume increases and if temperature decreases, volume decreases

Charles’ Law Example Problem • A gas occupies 152 m. L at 18 °C. How much space will the gas occupy at 36 °C? V 1 = V 2 T 1 T 2 (152 m. L) = V 2 2 (18 °C + 273) (36 °C + 273) (152 m. L) = V 2 2 (291 K) (309 K) (152 m. L)(309 K)= V 2(309 K) 2 (291 K) (309 K) (152 m. L)(309 K)= V 2 (291 K) 161 m. L = V 2

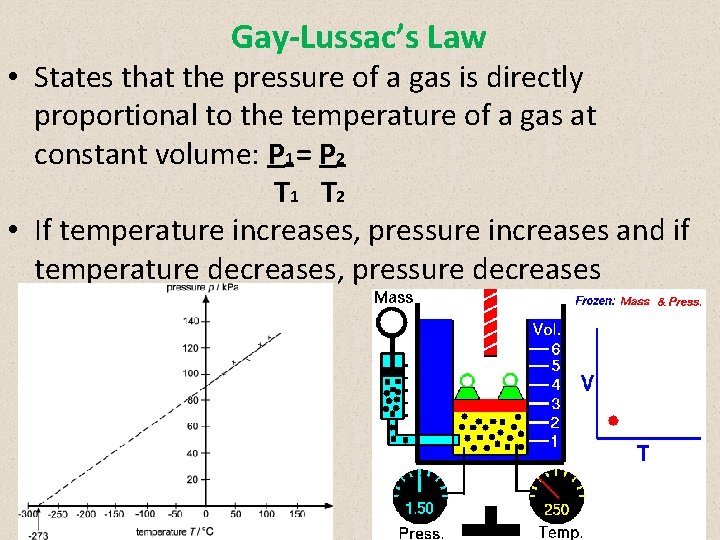
Gay-Lussac’s Law • States that the pressure of a gas is directly proportional to the temperature of a gas at constant volume: P 1 = P 2 T 1 T 2 • If temperature increases, pressure increases and if temperature decreases, pressure decreases

Gay-Lussac’s Law Example Problem • The pressure of a gas in a confined container is 237 k. Pa at 48 °C. What will the temperature be in degrees Celsius if the pressure changes to 142 k. Pa? P 1 = P 2 T 1 T 2 (237 k. Pa) = (142 k. Pa) (48 °C + 273) T 2 (237 k. Pa)(T 2) = (142 k. Pa)(T 2) (321 K) T 2 (237 k. Pa)(T 2)(321 K) = (142 k. Pa)(321 K)(237 k. Pa) T 2 = 192 K - 273 T 2 = -81 °C

Combined Gas Law • The Combined Gas law is a law that combines Charles's law, Boyle's law, and Gay-Lussac's law: P 1 V 1 = P 2 V 2 T 1 T 2 • In order for the Combined Gas Law to work, the moles of the gas need to be held constant

Combined Gas Law Example Problem • A gas at 110 k. Pa and 30. 0 C fills a 2. 00 L flexible container. If the temperature is raised to 80. 0 C and the pressure increases to 440 k. Pa, what will be the new volume? P 1 V 1 = P 2 V 2 T 1 T 2 (110 k. Pa)(2. 00 L) = (440 k. Pa)V 2 (30. 0 C + 273) (80. 0 C + 273) (110 k. Pa)(2. 00 L) (353 K) = (440 k. Pa)V 2(353 K) (303 K) (440 k. Pa) (353 K)(440 k. Pa) (110 k. Pa)(2. 00 L) (353 K) = V 2 (303 K) (440 k. Pa) 5. 83 x 10 -1 L = V 2

Avogadro’s Principle (Gas Stoichiometry) • States that equal volumes of gases at the same temperature and pressure contain equal numbers of moles of particles: 1 mol = 1 L • Standard Temperature and Pressure (STP) = 0. 00 C or 273 K and 1. 00 atm • At STP conditions: 1 mol gas = 22. 4 L (molar volume) Assuming ideal gas behavior • Allows us to convert moles of gas to liters (volume) of gas by using gas stoichiometry!

Avogadro’s Principle (Gas Stoichiometry) Example Problem • How many grams of oxygen gas is needed for the complete combustion of 4. 00 L of propane gas at STP represented by the unbalanced equation: C 3 H 8(g) + O 2(g) CO 2(g) + H 2 O(g) C 3 H 8(g) + 5 O 2(g) 3 CO 2(g) + 4 H 2 O(g) 4. 00 L C 3 H 8 x = 20. 0 L O 2 x x 28. 57 g O 2 =

Ideal Gas Law • To solve problems involving grams or moles of a gas, scientists must use the Ideal Gas Law: PV = n. RT • P = pressure in atm, k. Pa, torr, or mm Hg • V = volume in liters • n = moles of gas • T = temperature in Kelvin • R = ideal gas constant (value depends on pressure units) Pressure Unit Ideal Gas Constant Unit ((L x atm)/(mol x K)) atm 0. 0821 ((L x k. Pa)/(mol x K)) k. Pa 8. 314 ((L x torr)/(mol x K)) torr/mm Hg 62. 363

Ideal Gas Law Example Problem • What is the volume of 486 grams of oxygen gas at STP? 486 g O 2 x = 15. 2 mol O 2 PV = n. RT (1 atm)V = (15. 2 mol)(0. 0821)(273 K) (1 atm) V = 341 L

Avogadro’s Principle (Gas Stoichiometry) More Difficult Example Problem • Ammonia gas (NH 3) is synthesized from hydrogen and nitrogen gases. If 5. 00 L of nitrogen gas react completely at constant pressure of 3. 00 atm and constant temperature of 298 K how many grams of ammonia are produced? 3 H 2(g) + N 2(g) 2 NH 3(g) 5. 00 L N 2 x = 10. 0 L NH 3 : PV=n. RT (3. 00 atm)(10. 0 L) = n(0. 0821)(298 K) n = 1. 23 mol NH 3 x = 21. 0 g NH 3

Reminders for Solving Gas Law Problems • Write down all the known and unknown variables BEFORE solving. • Determine if any variables are being held constant because they can be eliminated from the combined gas law. • Make sure you convert all temperatures to Kelvin! • Remember what special conditions are true at STP!