Statecharts for the many Algebraic State Transition Diagrams

Statecharts for the many: Algebraic State Transition Diagrams Marc Frappier GRIL – Groupe de recherche en ingénierie du logiciel 1

Plan n Statecharts and information system specifications n ASTD : Algebraic State Transition Diagrams n Semantics of ASTD n Conclusion 2

Statecharts graphical notation n hierarchy + orthogonality n hierarchical states n AND states (parallel) n OR states (choice) n nice for single instance behaviour n parameterized states in Harel’s seminal paper (SCP 87) n n “never ” implemented or formalised 3

A library in statecharts 4

Problems n only describes behaviour of a single book n how to deal with several books? n put n copies of book n n n in parallel not defined in statecharts or UML available in ROSE RT, but it is not quite what we want here can discard an unreturned book n could add a guard to discard n unnecessary complexity n could make discard a transition from an inner state of loan n introduce coupling between book and loan 5

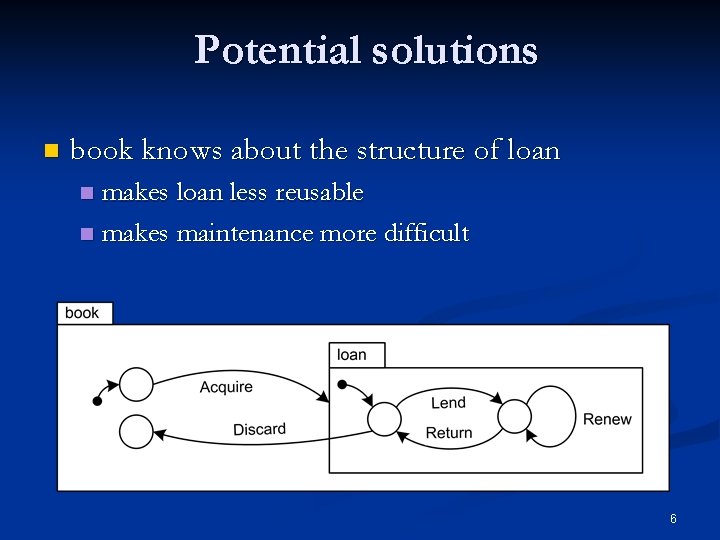
Potential solutions n book knows about the structure of loan makes loan less reusable n makes maintenance more difficult n 6

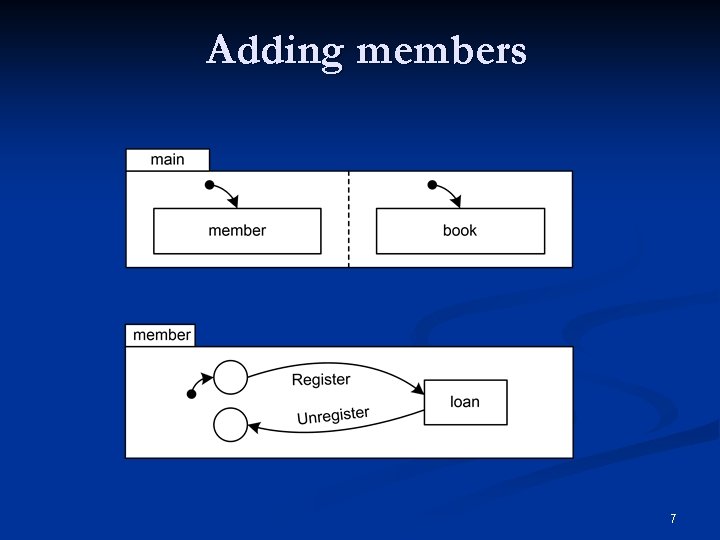
Adding members 7

Problems n a member can borrow several books in parallel n can’t “easily” express that in statecharts or UML n n State explosion two calls to loan n one in member, one in book n they both get the lend event OK if only one member KO if we have several members trying to borrow the same book n n n could remove loan from member n n must add guard to Unregister to check for completed loan loose visual ordering constraint 8

Potential solutions n remove loan from member n loose visual ordering constraint between member and loan n replaced by a guard n need state variable 9

The single instance view: A weakness of statecharts n both statecharts and UML state machines are designed to represent a single instance n eg, controller, object of a class, etc they offer no convenient means to express relationships between multiple instances n in practice, designers only describe the single instance behaviour n n leave it to the implementer to figure out the multiple instance case 10

A solution: Process algebra CCS, CSP, ACP, LOTOS, EB 3, . . . n algebra n n operators to combine process expressions n sequence, choice, interleave, synchronisation, guard, . . . n quantification n operators are the essence of abstraction n combine small units to build large units n operators foster abstraction by masking internal details 11

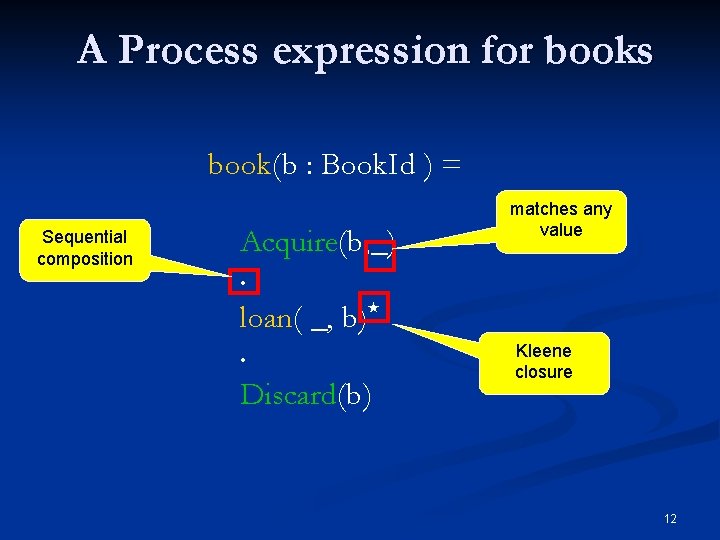
A Process expression for books book(b : Book. Id ) = Sequential composition Acquire(b, _) matches any value • loan( _, b) • Discard(b) Kleene closure 12

A process expression for loans loan(m. Id: Member, IDb. Id: Book. ID ) = guard nb. Loans(m. Id) < max. Nb. Loans(m. Id) Lend(m. Id, b. Id) • Renew(b. Id) • Return(b. Id) 13

A process expression for members member(m : Member. Id ) = Register(m, _, _) • ( b : Book. Id : loan( m, b) ) • Unregister(m) interleave quantification over all books 14

Interleave quantification x : {1, 2, 3} : P(x) = P(1) P(2) P(3) 15

Main process expression main = ( b : Book. Id : book(b) ) ( m : Member. Id : member(m) ) Synchronisation over common actions 16

Synchronisation over common actions a(1) • b(1) • c(1) quantified choice |x : T : a(x) • b(x) • c(2) = a(1) • b(1) • STOP 17

ASTD Algebraic State Transition Diagrams n ASTD = statecharts + process algebra n graphical notation n power of abstraction n n statecharts become elementary process expressions n n combine them using operators formal semantics n operational semantics 18

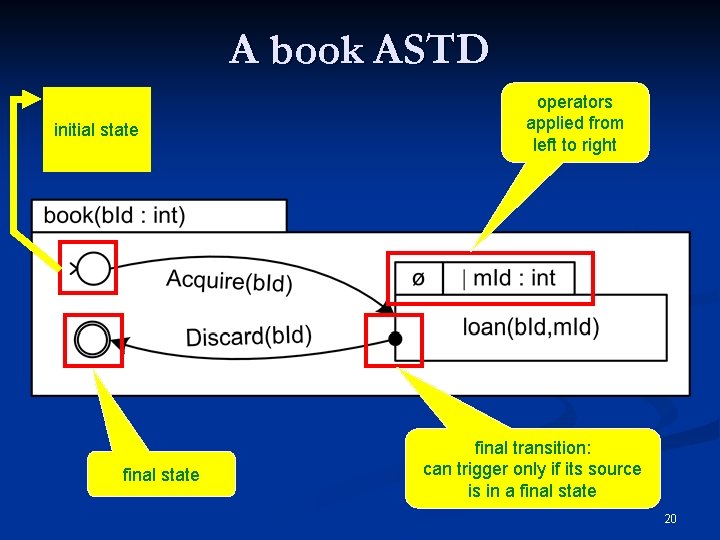
A book ASTD initial state final state operators applied from left to right final transition: can trigger only if its source is in a final state 20

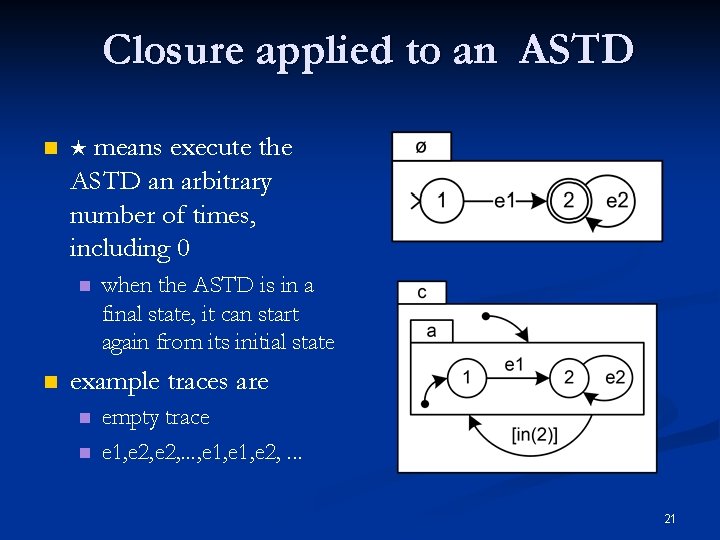
Closure applied to an ASTD n means execute the ASTD an arbitrary number of times, including 0 n n when the ASTD is in a final state, it can start again from its initial state example traces are n n empty trace e 1, e 2, . . . , e 1, e 2, . . . 21

The closure ASTD type ( , body ) n denotes the type constructor for a closure n body is an ASTD (of any type) 22

The closure state type n ০ is the closure state type constructor n started? is a boolean value that indicates if its component has started its first iteration s is the state of its component n ( ০ , started? , s ) 23

function that defines the initial state of an ASTD n closure ASTD initial state n n States of a closure initial state is the initial state of its component final states its initial state n final states of its component n function that determines if a state is final 24

Final state an ASTD does not terminate when its current state is final n a final state simply enables transitions of another ASTD within a n closure n sequence n 25

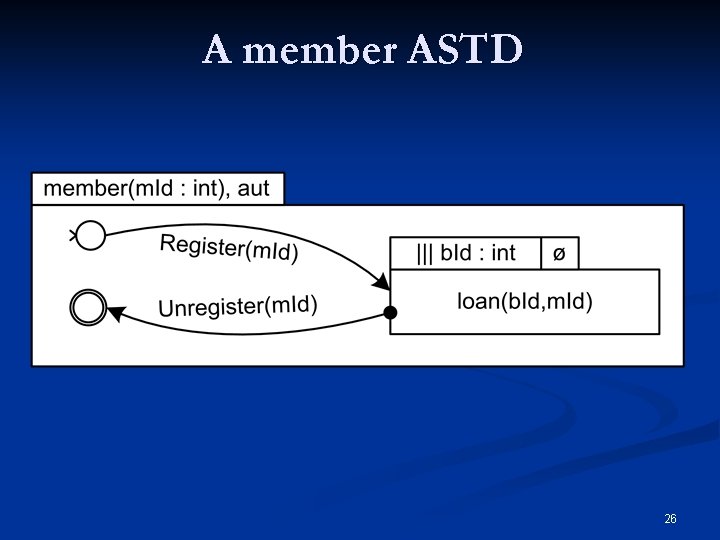
A member ASTD 26

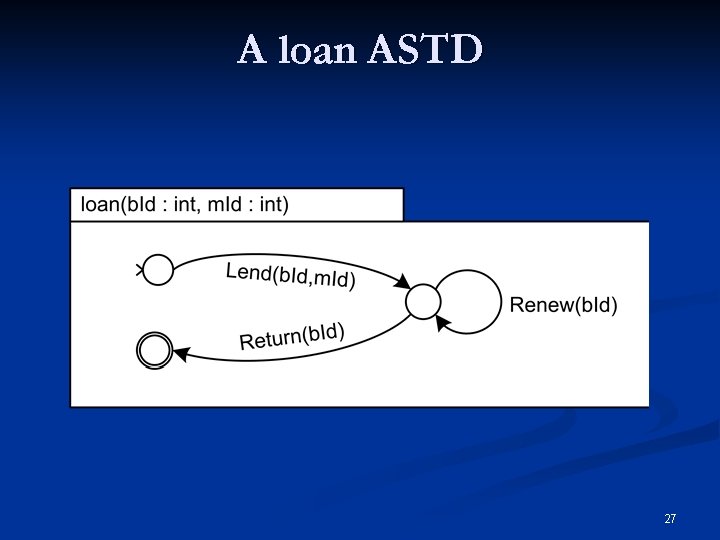
A loan ASTD 27

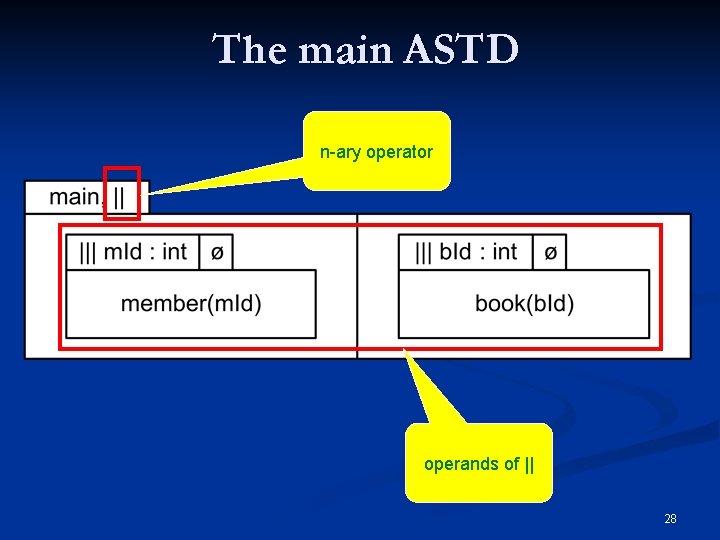
The main ASTD n-ary operator operands of || 28

Power of abstraction suppose you have two statecharts, a and b n you want to compose them as follows n execute a an arbitrary number of times n then execute b an arbitrary number of times n then start over again, an arbitrary number of times n n can’t do it in statecharts without peeking into a and b’s structure with guards n introduce a dependency between the compound and the components 29

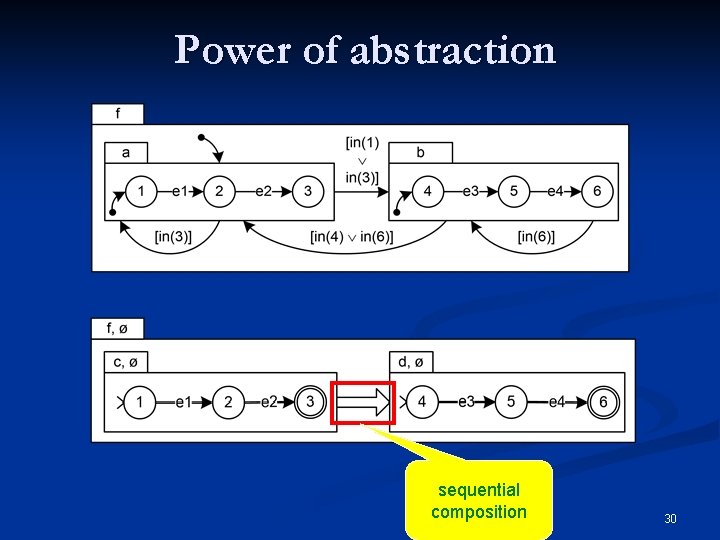
Power of abstraction sequential composition 30

The sequence ASTD type ( , left, right) n n denotes the sequence ASTD type constructor left and right are ASTDs 31

The sequence state type n n ০ denotes the sequence state type constructor side denotes the current side of the sequence n n n left right ( ০, side, s) s denotes the state of the side component 32

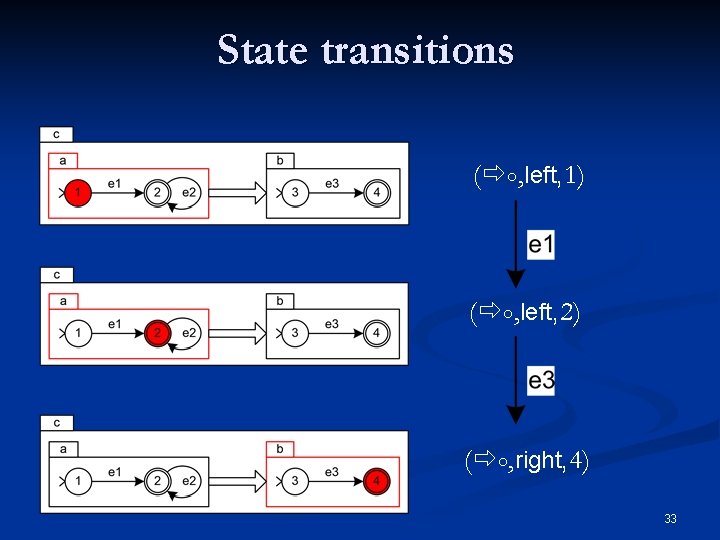
State transitions ( ০, left, 1) ( ০, left, 2) ( ০, right, 4) 33

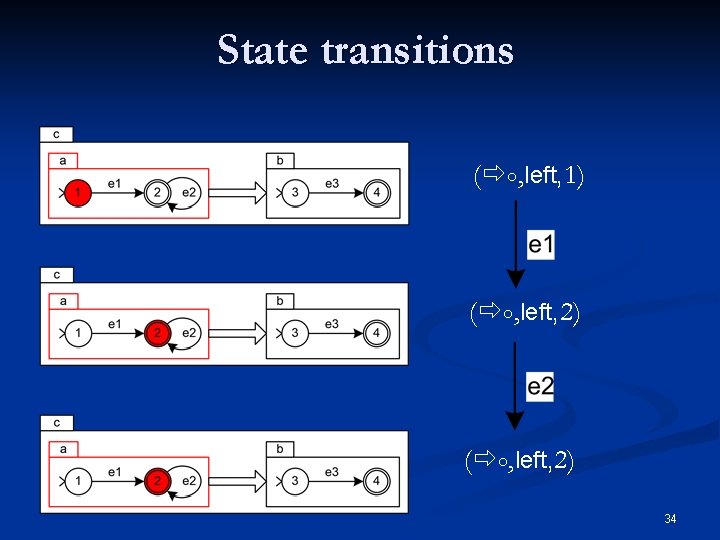
State transitions ( ০, left, 1) ( ০, left, 2) 34

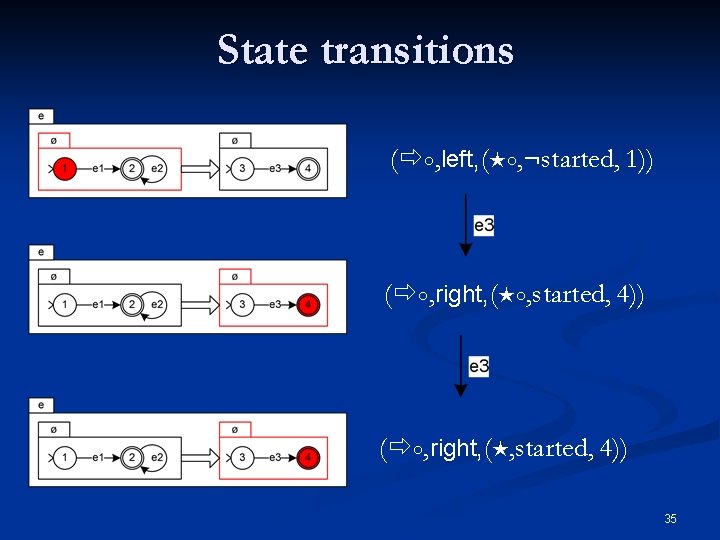
State transitions ( ০, left, ( ০, started, 1)) ( ০, right, ( ০, started, 4)) ( ০, right, ( , started, 4)) 35

Initial and final states of a sequence ASTD 36

Operational semantics first used by Milner for CCS n transitions n n ASTD a can execute from state s and move to state s’ 37

Operational semantics transitions defined by a set of inference rules n rules for each operator n allows non-determinism n if several transitions can fire from s, then one is nondeterministically chosen n no priority n 38

Inference rules n first rules deals with environment, noted ([ ]), to manage variables introduced by quantifications n process parameters n 39

similar to traditional Automaton inference rules of an automaton execute an automaton transition execute a transition of the component 40

Closure inference rules execute from the initial state of the component execute the component when started 41

Sequence inference rules execute on left execute on right when left is final execute the right component 42

Choice: initial and final states Choice state (|০, side, s) 43

Choice inference rules execute the first component from its initial state execute the second component from its initial state execute the first component when it has been selected execute the second component when it has been selected 44

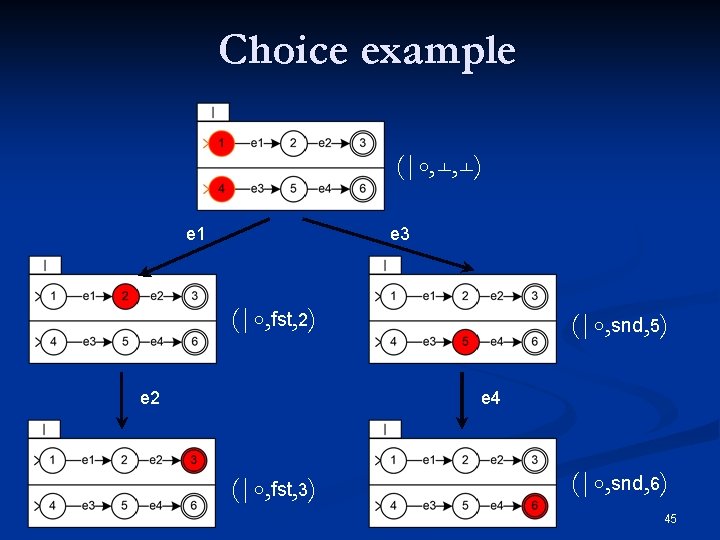
Choice example (|০, , ) e 1 e 3 (|০, fst, 2) e 2 (|০, snd, 5) e 4 (|০, fst, 3) (|০, snd, 6) 45

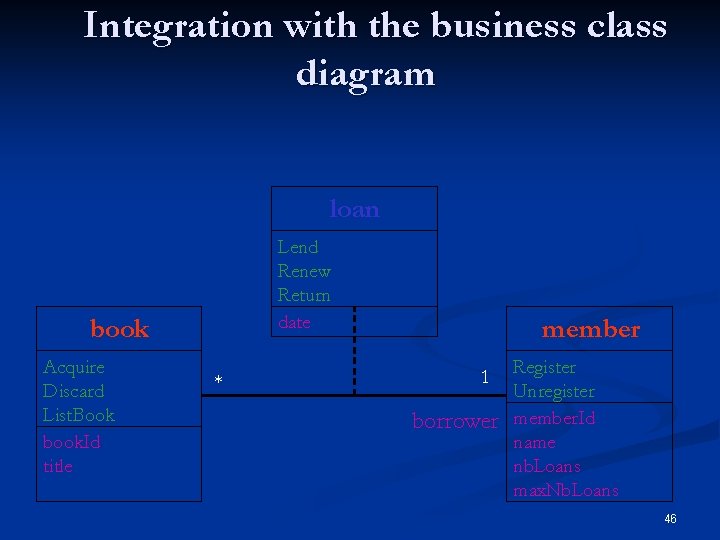
Integration with the business class diagram loan Lend Renew Return date book Acquire Discard List. Book book. Id title * member 1 borrower Register Unregister member. Id name nb. Loans max. Nb. Loans 46

State variables the system trace is the only state variable n entity attributes are functions on this trace n attributes can be used anywhere in ASTDs n n guard, quantification sets, . . . nb. Loans(m. Id : Member. Id) = Register(m. Id, _ ) : 0, Lend(m. Id, _) : 1 + nb. Loans(m. Id), Return(b. Id) : if borrower(b. Id) = m. Id then nb. Loans(m. Id) - 1, Unregister(m. Id, _ ) : ; 47

Conclusion n n process algebra operators can improve the expressiveness of statecharts complete, precise models of information systems n n not just single instance scenarios, but also multiple instance scenarios future work n n n tools for animation model checking code generation 48