STATE PLANE COORDINATE COMPUTATIONS Lectures 14 15 GISC3325

STATE PLANE COORDINATE COMPUTATIONS Lectures 14 – 15 GISC-3325

Updates and details ● Required reading assignments due 30 April 2008 ● Extra credit due 23 April 2008 ● ● Overdue lab assignments/homework will be given credit ONLY if received by 21 April 2008. Wednesday class: 16 April 2008 will be devoted to RTK. Mr. Toby Stock will demonstrate, make observations and show results. Meet him at Blucher during lecture and lab periods.

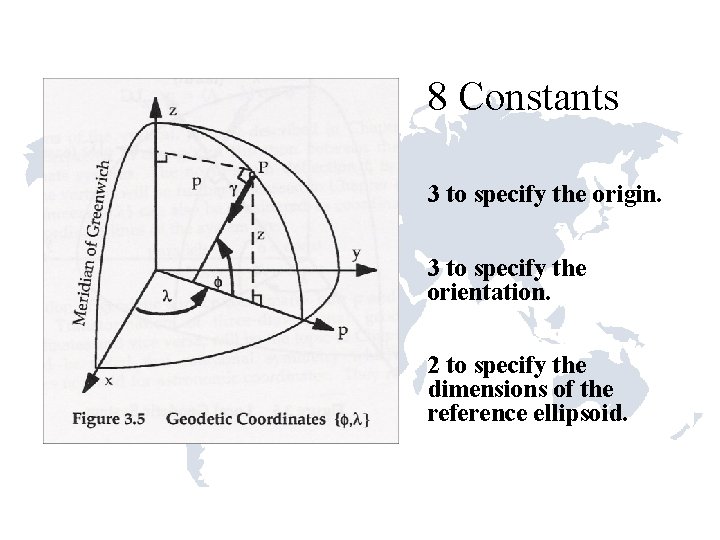
Datum: A set of constants specifying the coordinate system used to calculate coordinates of points on the Earth.

8 Constants 3 to specify the origin. 3 to specify the orientation. 2 to specify the dimensions of the reference ellipsoid.

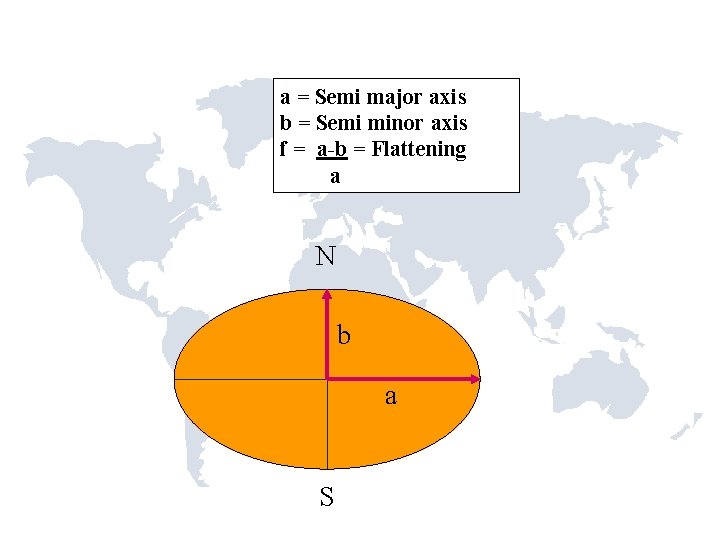
a = Semi major axis b = Semi minor axis f = a-b = Flattening a N b a S

BESSEL 1841 a = 6, 377, 397. 155 m 1/f = 299. 1528128 CLARKE 1866 a = 6, 378, 206. 4 m 1/f = 294. 97869821 GEODETIC REFERENCE SYSTEM 1980 - (GRS 80) a = 6, 378, 137 m 1/f = 298. 257222101 WORLD GEODETIC SYSTEM 1984 - (WGS 84) a = 6, 378, 137 m 1/f = 298. 257223563

Image on left from Geodesy for Geomatics and GIS Professionals by Elithorp and Findorff, Original. Works, 2004.

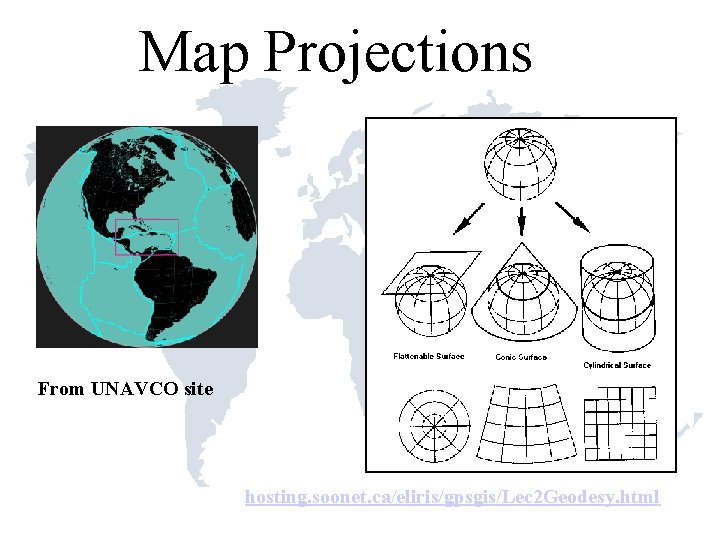
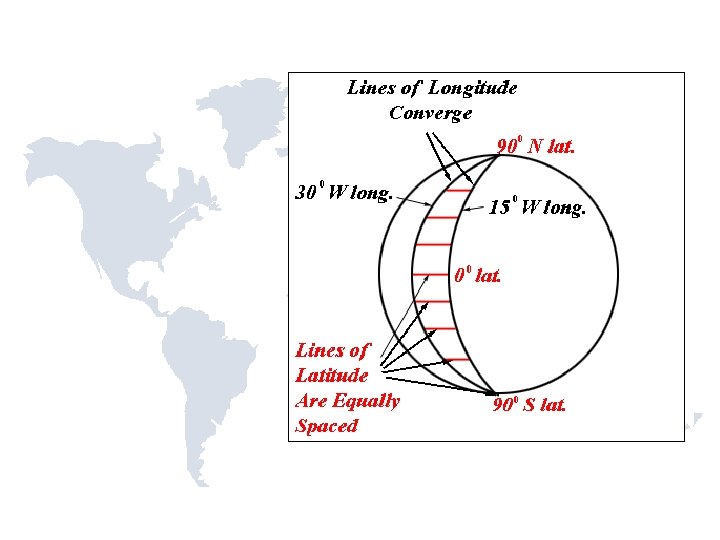
Map Projections From UNAVCO site hosting. soonet. ca/eliris/gpsgis/Lec 2 Geodesy. html

Taken from Ghilani, SPC

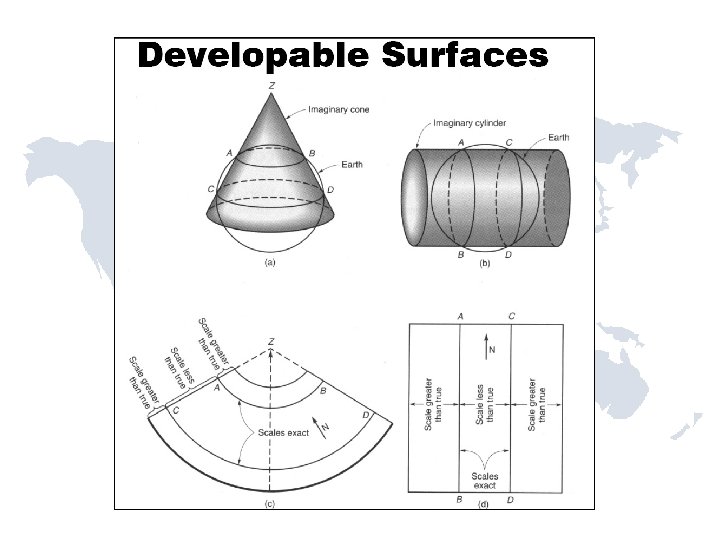
Conformal Mapping Projections ● ● Mapping a curved Earth on a flat map must address possible distortions in angles, azimuths, distances or area. Map projections where angles are preserved after projection are called “conformal”

http: //www. cnr. colostate. edu/class_info/nr 502/lg 3/datums_coordinates/spcs. html

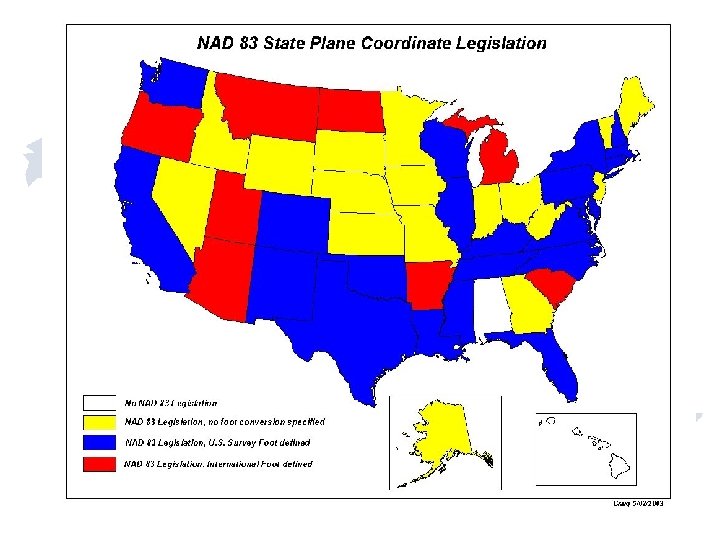
• SPCS 27 designed in 1930 s to facilitate the attachment of surveys to the national system. • Uses conformal mapping projections. • Restricts maximum scale distortion to less than 1 part in 10 000. • Uses as few zones as possible to cover a state. • Defines boundaries of zones on countybasis.

http: //www. ngs. noaa. gov/PUBS_LIB/pub_index. html

Source: http: //www. cnr. colostate. edu/class_info/nr 502/lg 3/datums_coordinates/spcs. html

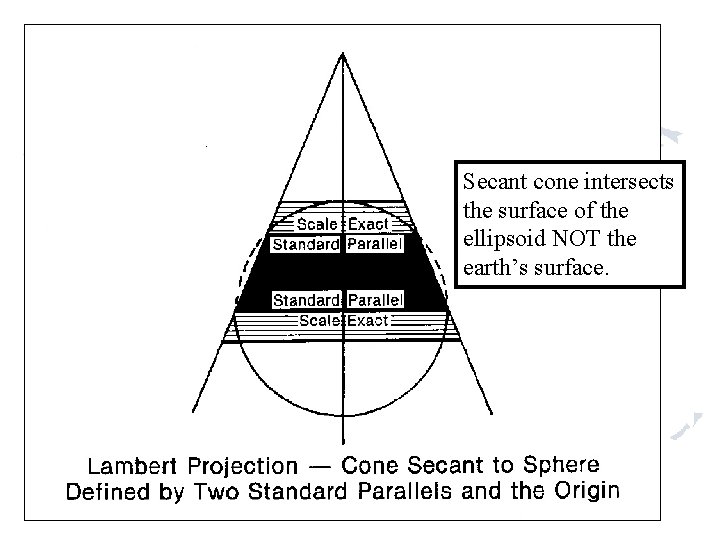
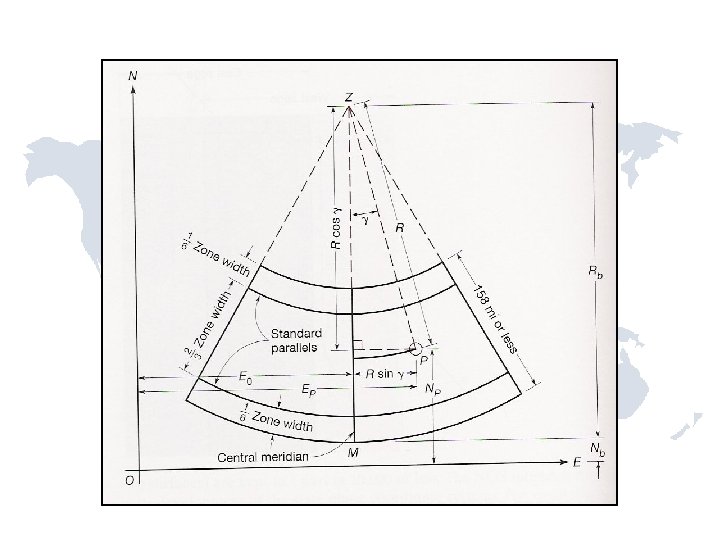
Secant cone intersects the surface of the ellipsoid NOT the earth’s surface.

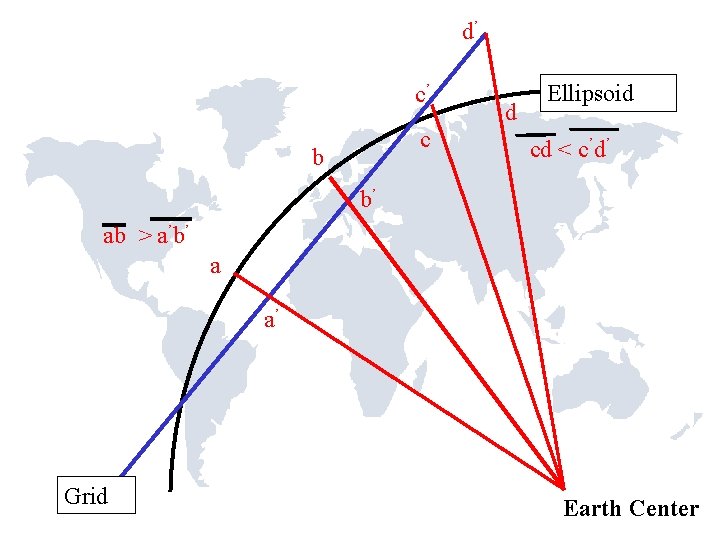
d’ c’ c b d Ellipsoid cd < c’d’ b’ ab > a’b’ a a’ Grid Earth Center

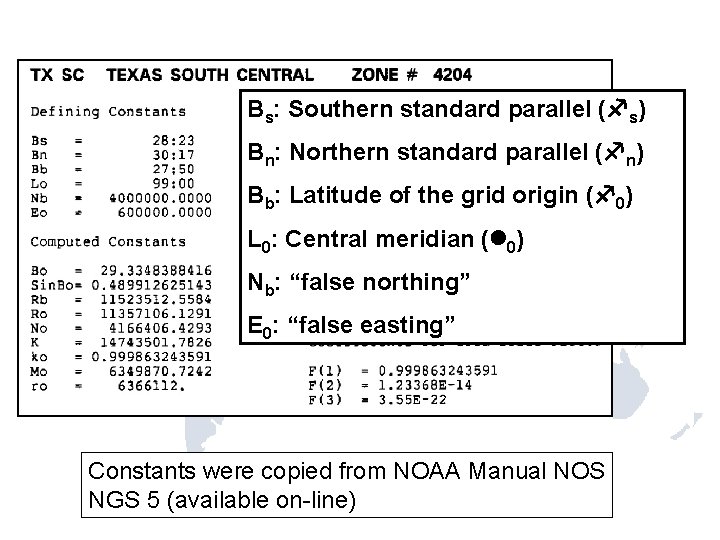
Bs: Southern standard parallel ( s) Bn: Northern standard parallel ( n) Bb: Latitude of the grid origin ( 0) L 0: Central meridian ( 0) Nb: “false northing” E 0: “false easting” Constants were copied from NOAA Manual NOS NGS 5 (available on-line)

Zone constant computations Latitude of grid origin Mapping radius at equator. Equations from NGS manual, SPCS of 1983 NOS NGS 5

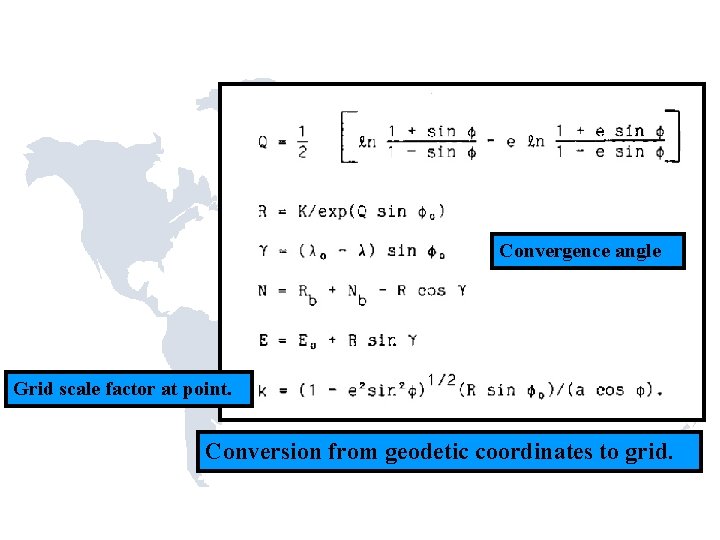
R 0: Mapping radius at latitude of true projection origin. k 0: Grid scale factor at CM. N 0: Northing value at CM intersection with central parallel.

Convergence angle Grid scale factor at point. Conversion from geodetic coordinates to grid.

Formulas converted to Matlab script.

Grid to Geodetic Coordinates

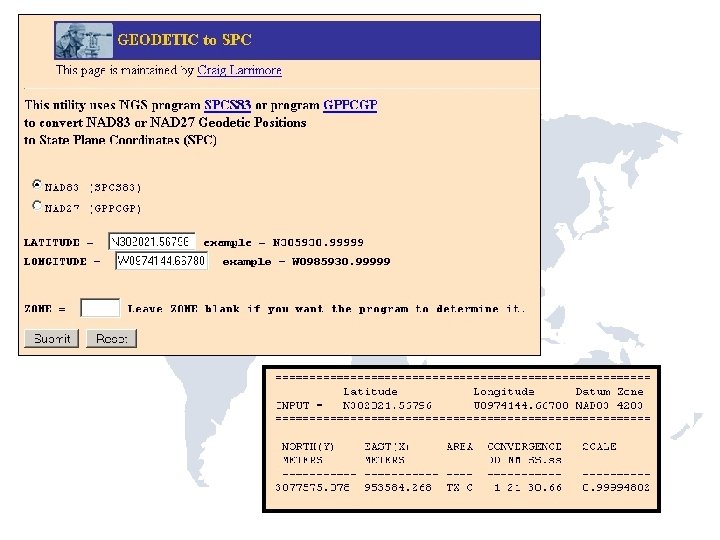
http: //www. ngs. noaa. gov/TOOLS/spc. shtml

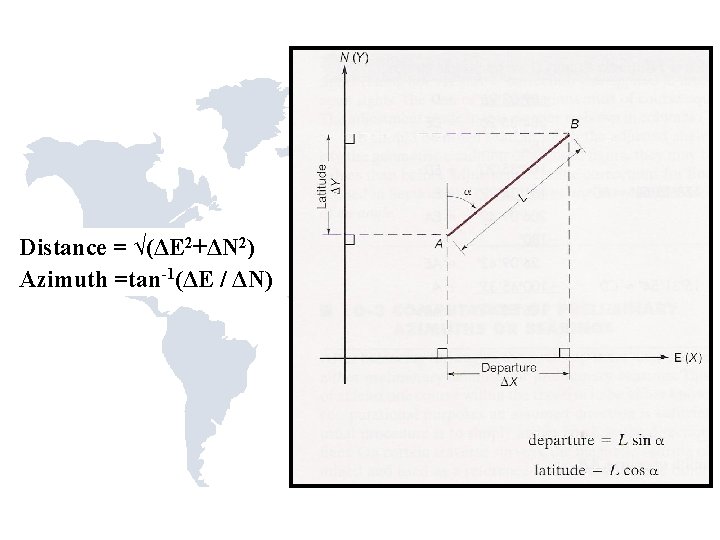
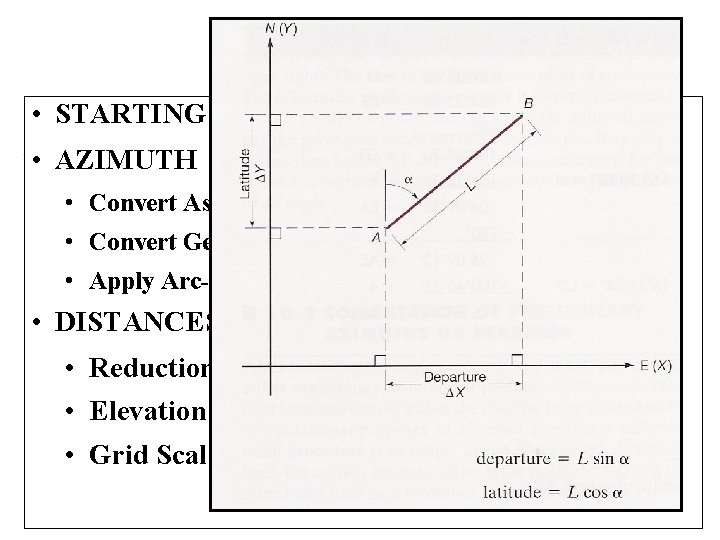
Distance = √(ΔE 2+ΔN 2) Azimuth =tan-1(ΔE / ΔN)

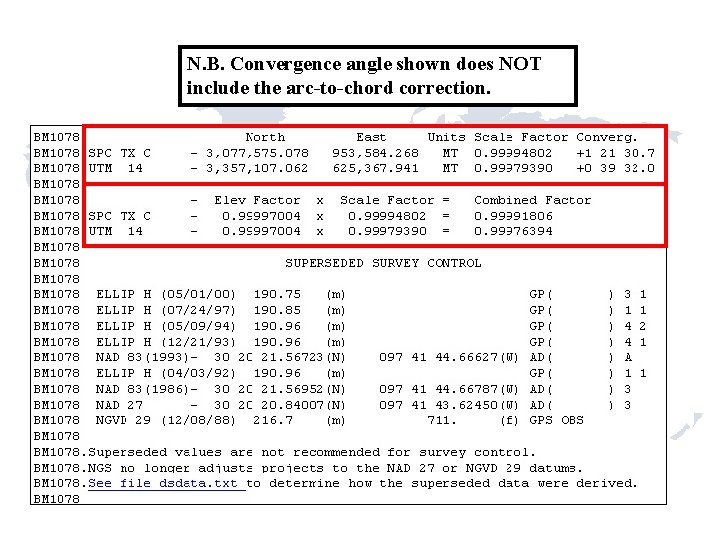
N. B. Convergence angle shown does NOT include the arc-to-chord correction.

• STARTING COORDINATES • AZIMUTH • Convert Astronomic to Geodetic • Convert Geodetic to Grid (Convergence angle) • Apply Arc-to-Chord Correction (t-T) • DISTANCES • Reduction from Horizontal to Ellipsoidal • Elevation “Sea-Level” Reduction Factor • Grid Scale Factor

N = 3, 078, 495. 629 E= N= 924, 954. 270 -25. 13 k = 0. 99994523 Convergence angle +01 -12 -19. 0 LAPLACE Corr. -4. 04 seconds

Laplace correction ● ● ● Used to convert astronomic azimuths to geodetic azimuths. A simple function of the geodetic latitude and the eastwest deflection of the vertical at the ground surface. Corrections to horizontal directions are a function of the Laplace correction and the zenith angle between stations, and can become significant in mountainous areas.

Astronomic to Geodetic Azimuth ● ● ● =Φ–ξ = Λ - (η / cos ) α= A- η∙tan ( , ) are geodetic coordinates – (Φ, Λ) are astronomic coord. – (ξ, η) are the Xi and Eta corrections – (α, A) are geodetic and astronomic azimuths respectively) –

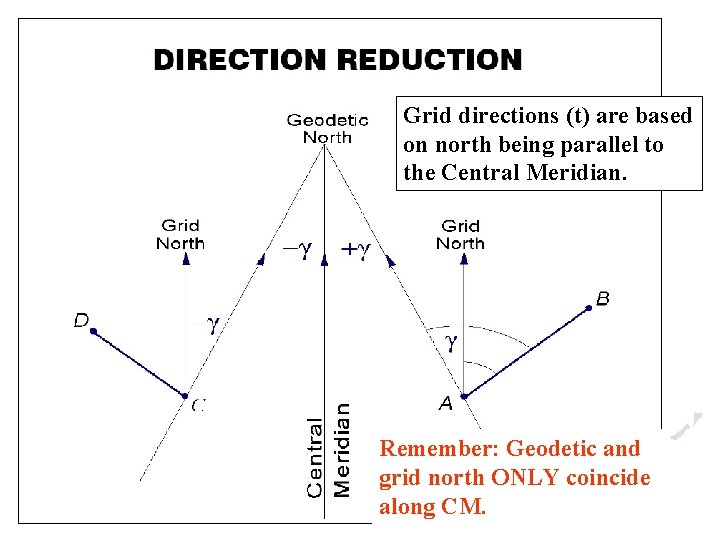
Grid directions (t) are based on north being parallel to the Central Meridian. Remember: Geodetic and grid north ONLY coincide along CM.

Astronomic to Grid (via geodetic) ag = a. A + Laplace Correction – g 253 d 26 m 14. 9 s - Observed Astro Azimuth + ( - 1. 33 s) - Laplace Correction 253 d 26 m 13. 6 s - Geodetic Azimuth + 1 12 m 19. 0 s - Convergence Angle (g) 254 d 38 m 32. 6 s - Grid azimuth The convention of the sign of the convergence angle is always from Grid to Geodetic.

Arc-to-Chord correction δ (alias t – T) • Azimuth computed from two plane coordinate pairs is a grid azimuth (t). • Projected geodetic azimuth is (T). • Geodetic azimuth is (α ) • Convergence angle (γ) is the difference between geodetic and projected geodetic azimuths. • Difference between t and T = “δ”, the “arc-tochord” correction, or “t-T” or “second-term” correction. ● t = α-γ+ δ

Arc-to-Chord correction δ (alias t – T) Where t is grid azimuth.

When should it be applied? ● ● Intended for during precise surveys. Recommended for use on lines over 8 kilometers long. It is always concave toward the Central Parallel of the projection. Computed as: δ = 0. 5(sin 3 -sin 0)( 1 - 2) – Where 3 = (2 1 + 2)/3 –

Compute magnitude of the secondterm correction from preliminary coordinates. It is not significant for short sight distances (< 8 km) but … The effect of this correction is cumulative! Azimuth of line from N Sign of N-N 0 Azimuth of line from N 0 to 180 to 360 Positive + - Negative - +

Angle Reductions ● Know the type of azimuth – – – ● ● ● Astronomic Geodetic Grid Apply appropriate corrections Angles (difference of two directions from a single station) do not need to consider convergence angle. Apply arc-to-chord correction for long sight distances or long traverses (cumulative effect).

N 1 = N + (Sg x cos ag) E 1 = E + (Sg x sin ag) Where: N = Starting Northing Coordinate E = Starting Easting Coordinates Sg = Grid Distance ag = Grid Azimuth

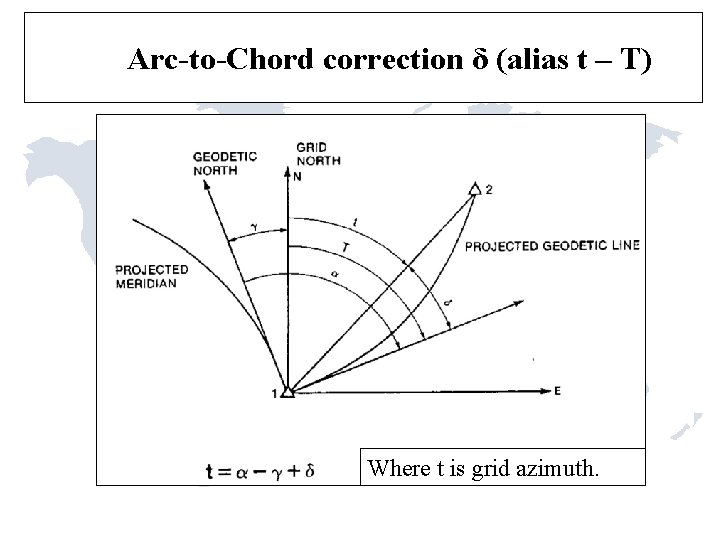
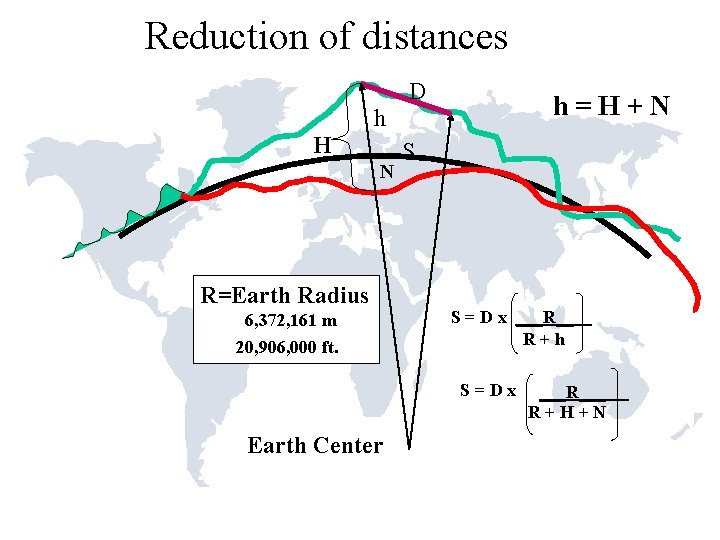
Reduction of Distances ● ● When working with geodetic coordinates use ellipsoidal distances. When working with state plane coordinates reduce the observations to the grid (mapping surface).

Re is the radius of the Earth in the azimuth of the line. Lm is surface Le is ellipsoid

For most surveys the approximate radius used in NAD 27 (6, 372, 000 m or 20, 906, 000 ft) can be used for Re.

Reduce ellipsoid distance to grid

Final reduced distance ● ● ● Measured distances are first corrected for atmospheric refraction and earth’s curvature. Distances reduced to ellipsoid. Distances reduced to grid by applying the combined factor (scale factor by elevation factor).

EF at a point (numeric example) Let R = 6372000, h = 48. 98 EF = R/(R + h) = 0. 999992313 if we do not have h, compute it via relationship: N + H

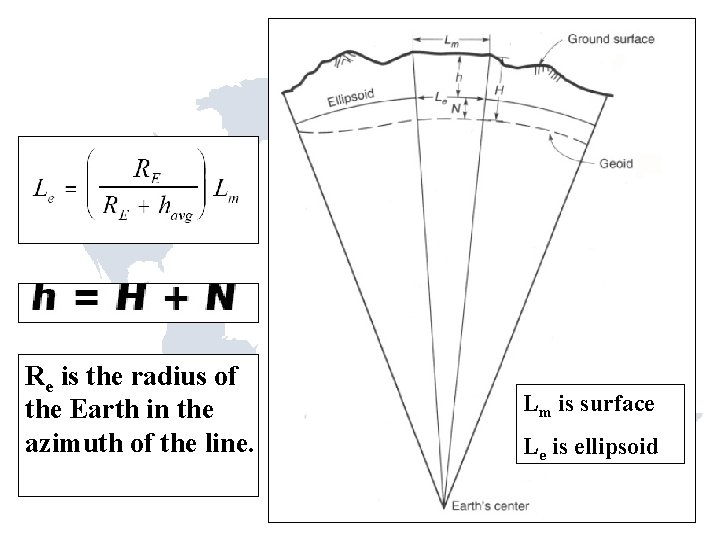
Reduction of distances D h=H+N h H N R=Earth Radius 6, 372, 161 m 20, 906, 000 ft. S S = D x ___R__ R+h S=Dx Earth Center ___R___ R+H+N

D 5 is the geodetic distance.

REDUCTION TO ELLIPSOID S = D x [R / (R + h)] D = 1010. 387 meters (Measured Horizontal Distance) R = 6, 372, 162 meters (Mean Radius of the Earth) h = H + N (H = 2 m, N = - 26 m) = - 24 meters (Ellipsoidal Height) S = 1010. 387 [6, 372, 162 / 6, 372, 162 - 24] S = 1010. 387 x 1. 00000377 S = 1010. 391 meters If N is ignored: S = 1010. 387 [6, 372, 162 / 6, 372, 162 + 2] S = 1010. 387 x 0. 99999969 S = 1010. 387 meters -- 0. 004 m or about 1: 252, 600

REDUCTION TO GRID Sg = S (Geodetic Distance) x k (Grid Scale Factor) Sg = 1010. 391 x 0. 99992585 = 1010. 316 meters

COMBINED FACTOR CF = Ellipsoidal Reduction x Grid Scale Factor (k) = 1. 00000377 x 0. 99992585 = 0. 99992962 CF x D = Sg 0. 99992962 x 1010. 387 = 1010. 316 meters

STATE PLANE COORDINATE COMPUTATION N 1 = N + (Sg x cos ag) E 1 = E + (Sg x sin ag) N 1 = 4, 103, 643. 392 + (1010. 277 x Cos 253 o 30’ 07. 4”) = 4, 103, 643. 392 + (1010. 277 x - 0. 28398094570069) = 4, 103, 643. 392 + (- 286. 899) = 4, 103, 356. 492 meters E 1 = 587, 031. 437 + (1010. 277 x Sin 253 o 30’ 07. 4”) = 587, 031. 437 + (1010. 277 x - 0. 95882992364597) = 587, 031. 437 + (- 968. 684) = 586, 062. 753 meters

“I WANT STATE PLANE COORDINATES RAISED TO GROUND LEVEL” GROUND LEVEL COORDINATES ARE NOT STATE PLANE COORDINATES!!!!!

PROBLEMS WITH GROUND LEVEL COORDINATES • RAPID DISTORTIONS • PROJECTS DIFFICULT TO TIE TOGETHER • CONFUSION OF COORDINATE SYSTEMS • LACK OF DOCUMENTATION

GROUND LEVEL COORDINATES “IF YOU DO” TRUNCATE COORDINATE VALUES SUCH AS: N = 13, 750, 260. 07 ft becomes 50, 260. 07 E= 2, 099, 440. 89 ft becomes 99, 440. 89 AND

GOOD COORDINATION BEGINS WITH GOOD COORDINATES GEOGRAPHY WITHOUT GEODESY IS A FELONY

The Universal Grids: Universal Transverse Mercator (UTM) and Universal Polar Stereographic (UPS) - TM 8358. 2 • Transverse Mercator Projection • Zone width 6 o Longitude World-Wide • Northing Origin (0 meters- Northern Hemisphere) at the Equator • Easting Origin (500, 000 meters) at Central Meridian of Each Zone