State of the art closed orbit feedback system

State of the art closed orbit feedback system Sajjad Hussain Mirza 1, 2 Rahul Singh 1 Peter Forck 1 1 Beam Instrumentation Group GSI, Darmstadt 2 TEMF, TU, Darmstadt Germany 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 1

Outline v Perturbed closed orbit : (examples) v Brief comparison for Hadron Machines and Light Sources : motivation v Components and key design players : orbit correction methods v Symmetry exploitation v Controller types v Spatial model mismatch v Closed orbit feedback system at SIS 18 : results of first test v Summary 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 2 S. H. Mirza

Closed orbit perturbation (examples) SIS 18 static orbit horizontal Schematic of closed orbit of SIS 18 synchrotron of GSI position [mm] 6 0 vertical -6 along synchrotron -12 Diamond light source static orbit SIS 18 orbit movement BPM 02 Closed orbit correction is the integral part of almost every synchrotron operation. Ph. D thesis, S. Gayadeen 11/26/202 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 3 S. H. Mirza

ARIES workshop on Next Generation Beam Position Acquisition and Feedback Systems v A unique platform for the interaction of COFB community from light sources and hadron synchrotrons. v Demands, achievements and challenges were discussed and compared for both kind of synchrotrons. v A possibility of transfer of knowledge from light sources to hadron machines for fast orbit feedback systems. 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 4 S. H. Mirza

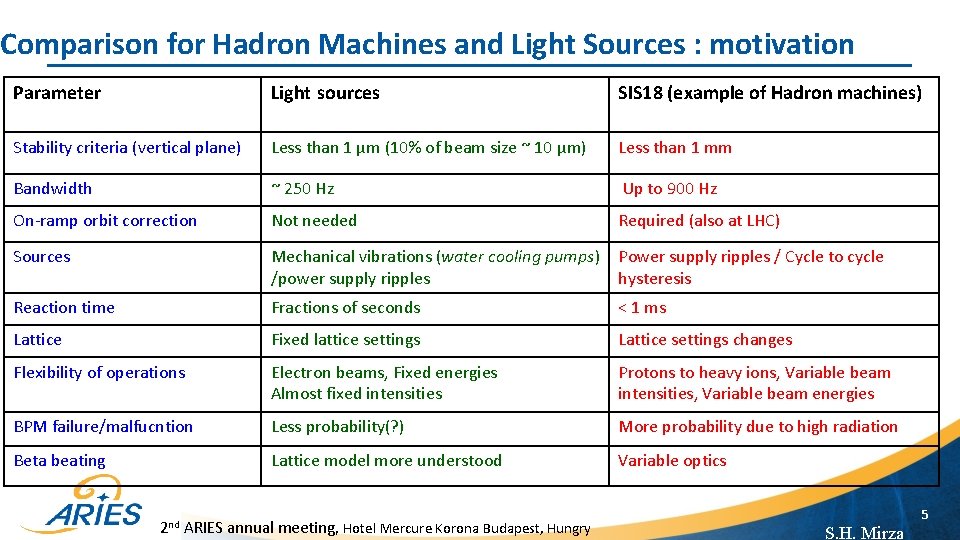
Comparison for Hadron Machines and Light Sources : motivation Parameter Light sources SIS 18 (example of Hadron machines) Stability criteria (vertical plane) Less than 1 μm (10% of beam size ~ 10 μm) Less than 1 mm Bandwidth ~ 250 Hz Up to 900 Hz On-ramp orbit correction Not needed Required (also at LHC) Sources Mechanical vibrations (water cooling pumps) Power supply ripples / Cycle to cycle /power supply ripples hysteresis Reaction time Fractions of seconds < 1 ms Lattice Fixed lattice settings Lattice settings changes Flexibility of operations Electron beams, Fixed energies Almost fixed intensities Protons to heavy ions, Variable beam intensities, Variable beam energies BPM failure/malfucntion Less probability(? ) More probability due to high radiation Beta beating Lattice model more understood Variable optics 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 5 S. H. Mirza

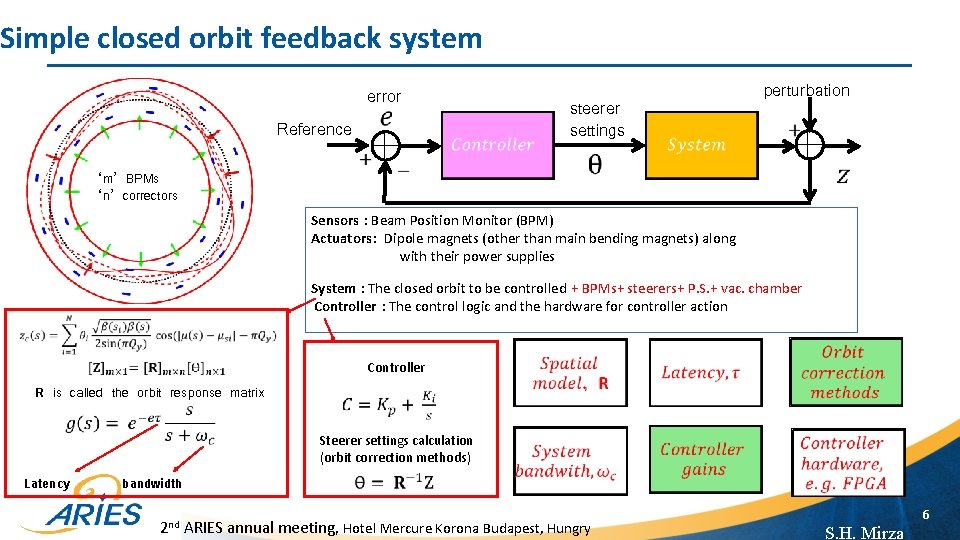
Simple closed orbit feedback system error Reference ‘m’ BPMs ‘n’ correctors steerer settings perturbation Sensors : Beam Position Monitor (BPM) Actuators: Dipole magnets (other than main bending magnets) along with their power supplies System : The closed orbit to be controlled + BPMs+ steerers+ P. S. + vac. chamber Controller : The control logic and the hardware for controller action Controller R is called the orbit response matrix bandwidth Steerer settings calculation (orbit correction methods) Latency 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 6 S. H. Mirza

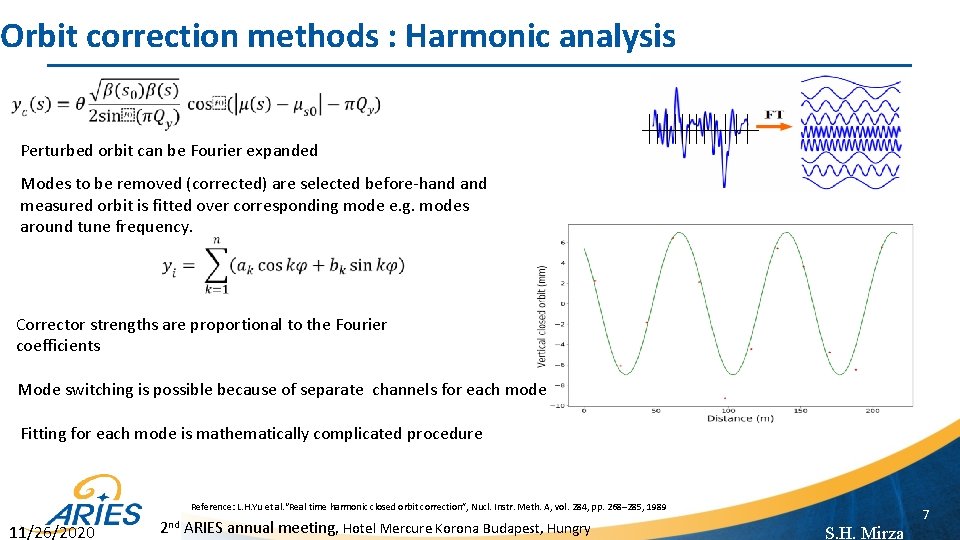
Orbit correction methods : Harmonic analysis Perturbed orbit can be Fourier expanded Modes to be removed (corrected) are selected before-hand measured orbit is fitted over corresponding mode e. g. modes around tune frequency. Corrector strengths are proportional to the Fourier coefficients Mode switching is possible because of separate channels for each mode Fitting for each mode is mathematically complicated procedure Reference: L. H. Yu et al. “Real time harmonic closed orbit correction”, Nucl. Instr. Meth. A, vol. 284, pp. 268– 285, 1989 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 7 S. H. Mirza

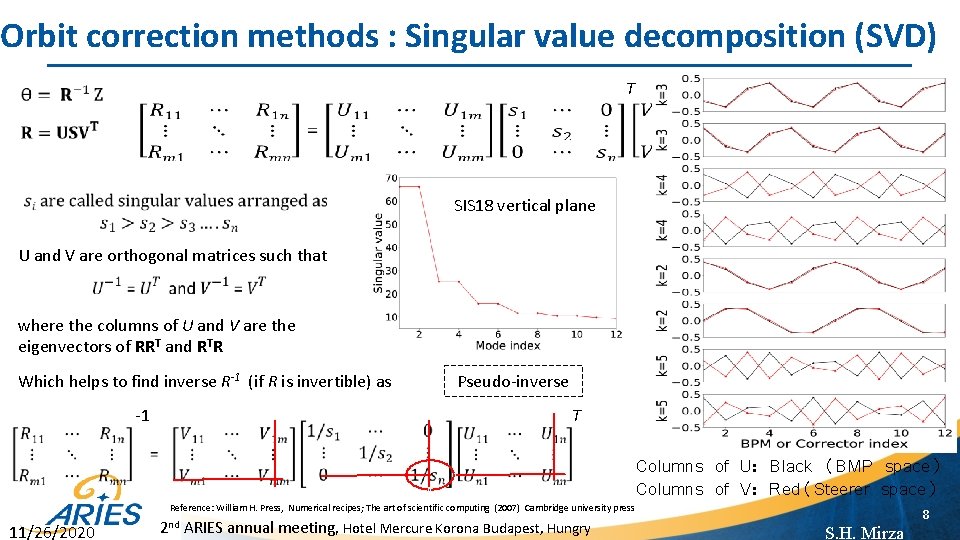
Orbit correction methods : Singular value decomposition (SVD) T SIS 18 vertical plane U and V are orthogonal matrices such that where the columns of U and V are the eigenvectors of RRT and RTR Which helps to find inverse R-1 (if R is invertible) as -1 Pseudo-inverse T Reference: William H. Press, Numerical recipes; The art of scientific computing (2007) Cambridge university press 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry Columns of U: Black (BMP space) Columns of V: Red(Steerer space) 8 S. H. Mirza

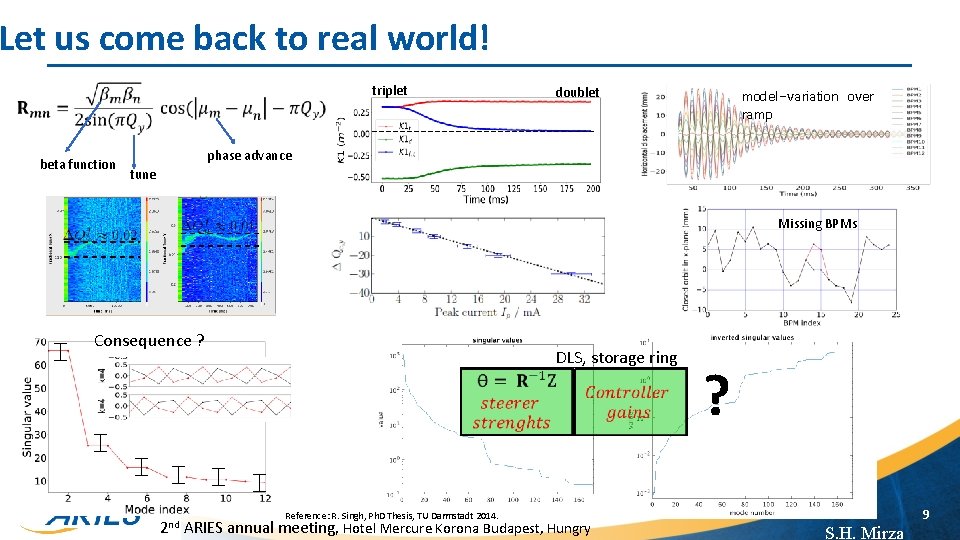
Let us come back to real world! triplet beta function doublet model-variation over ramp phase advance tune Missing BPMs Consequence ? DLS, storage ring ? 9 Reference: R. Singh, Ph. D Thesis, TU Darmstadt 2014. 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry S. H. Mirza

SVD in case of spatial model uncertainties v U and V are interconnected through a phase relation v Uncertainty modeling is required in all three matrices T k=3 v Over the ramp, updating of all three matrices required Qy = 3. 28 v Loss of physical interpretation of modes (SVD is a numerical technique) Fourier coefficients of harmonic analysis have been proposed for uncertainty modeling Tune mode, k=3 Qy = 3. 28 Reference: S. Gayadeen, “Synchrotron Electron Beam Control”, Ph. D. thesis, St. Hugh’s College, University of Oxford, UK, 2014. 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 10 S. H. Mirza

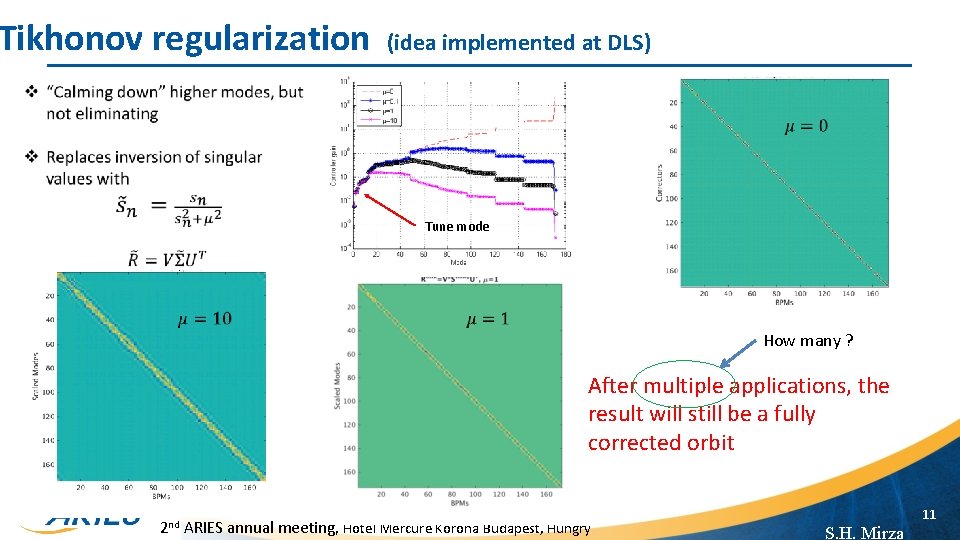
Tikhonov regularization (idea implemented at DLS) Tune mode How many ? After multiple applications, the result will still be a fully corrected orbit 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 11 S. H. Mirza

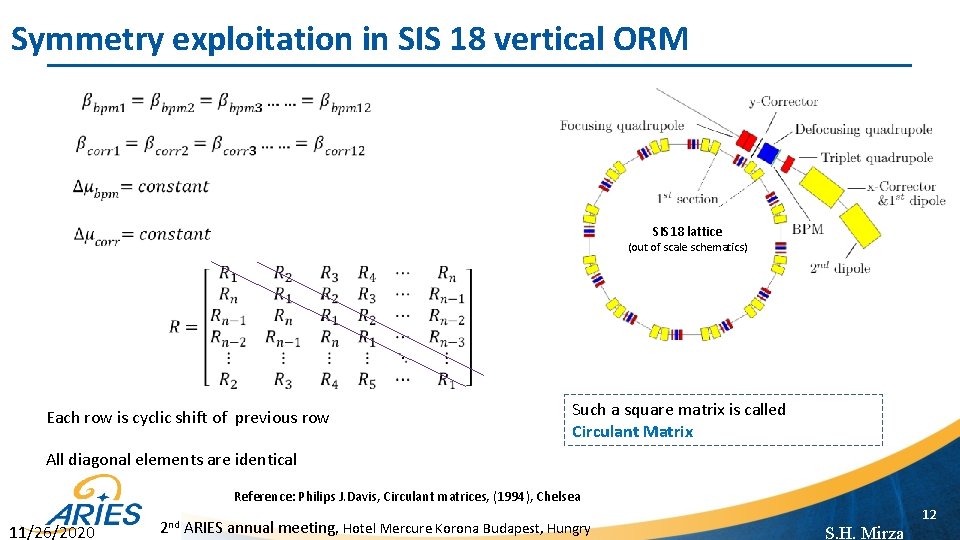
Symmetry exploitation in SIS 18 vertical ORM SIS 18 lattice (out of scale schematics) Each row is cyclic shift of previous row Such a square matrix is called Circulant Matrix All diagonal elements are identical Reference: Philips J. Davis, Circulant matrices, (1994), Chelsea 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 12 S. H. Mirza

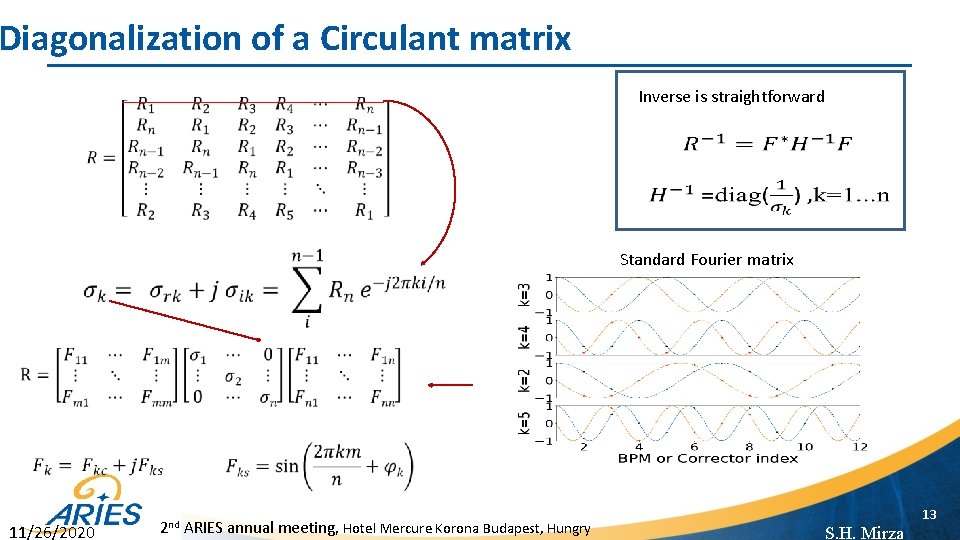
Diagonalization of a Circulant matrix Inverse is straightforward Standard Fourier matrix 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 13 S. H. Mirza

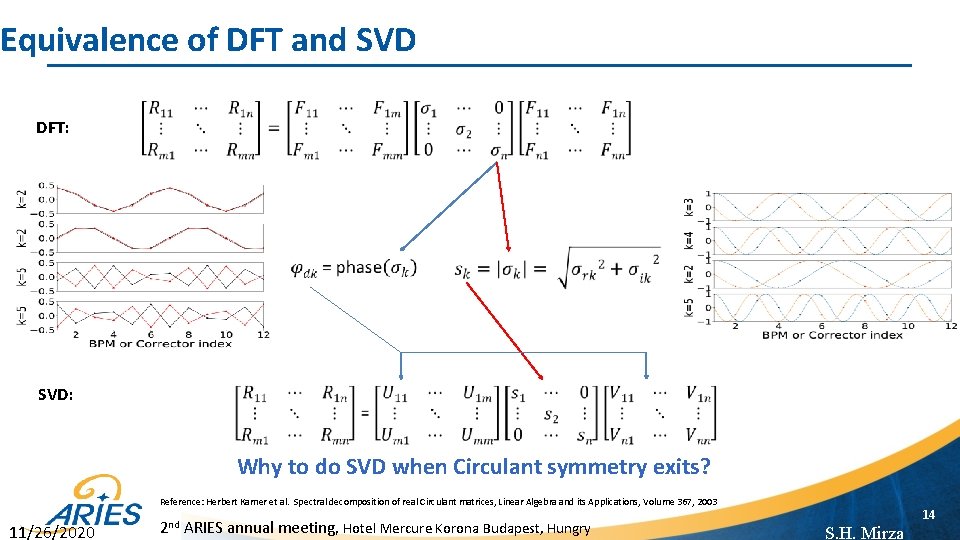
Equivalence of DFT and SVD DFT: SVD: Why to do SVD when Circulant symmetry exits? Reference: Herbert Karner et al. Spectral decomposition of real Circulant matrices, Linear Algebra and its Applications, Volume 367, 2003 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 14 S. H. Mirza

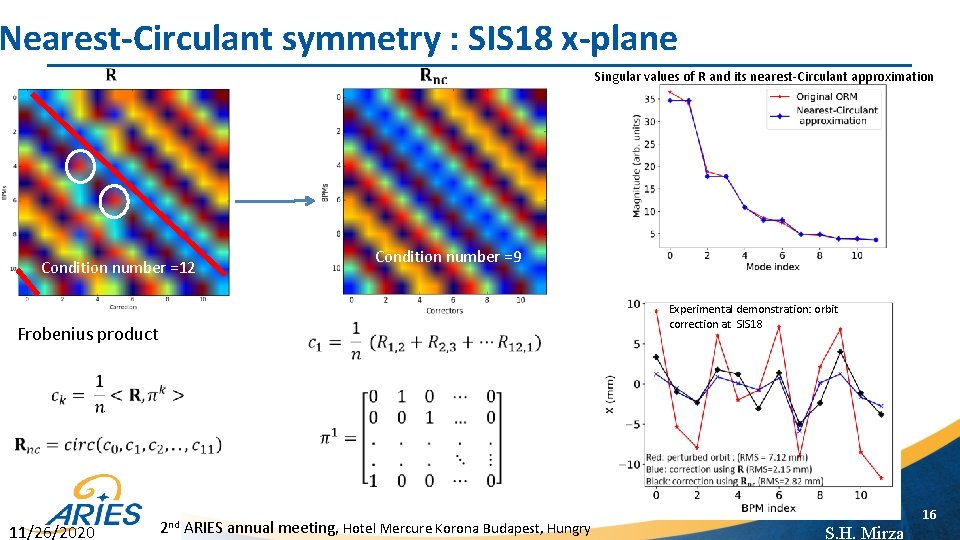
Nearest-Circulant symmetry : SIS 18 x-plane Condition number =9 Condition number =12 Frobenius product Experimental demonstration: orbit correction at SIS 18 11/26/2020 Singular values of R and its nearest-Circulant approximation 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 16 S. H. Mirza

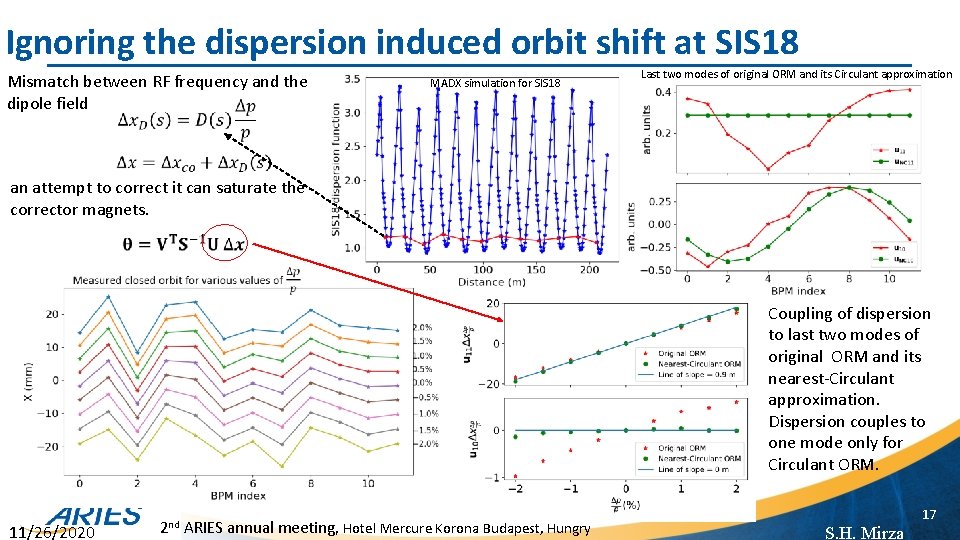
Ignoring the dispersion induced orbit shift at SIS 18 Mismatch between RF frequency and the dipole field MADX simulation for SIS 18 Last two modes of original ORM and its Circulant approximation an attempt to correct it can saturate the corrector magnets. Coupling of dispersion to last two modes of original ORM and its nearest-Circulant approximation. Dispersion couples to one mode only for Circulant ORM. 11/26/2020 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 17 S. H. Mirza

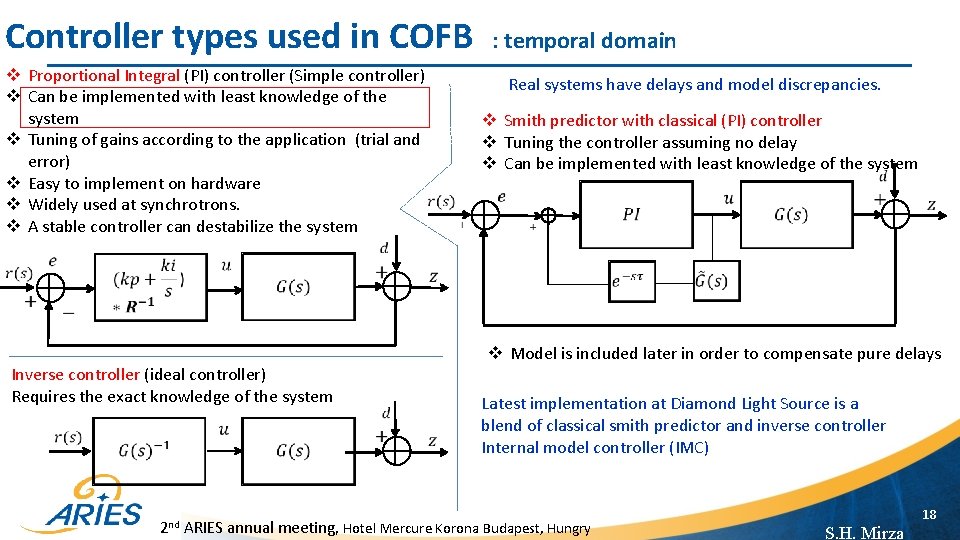
Controller types used in COFB v Proportional Integral (PI) controller (Simple controller) v Can be implemented with least knowledge of the system v Tuning of gains according to the application (trial and error) v Easy to implement on hardware v Widely used at synchrotrons. v A stable controller can destabilize the system : temporal domain Real systems have delays and model discrepancies. v Smith predictor with classical (PI) controller v Tuning the controller assuming no delay v Can be implemented with least knowledge of the system v Model is included later in order to compensate pure delays Inverse controller (ideal controller) Requires the exact knowledge of the system Latest implementation at Diamond Light Source is a blend of classical smith predictor and inverse controller Internal model controller (IMC) 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 18 S. H. Mirza

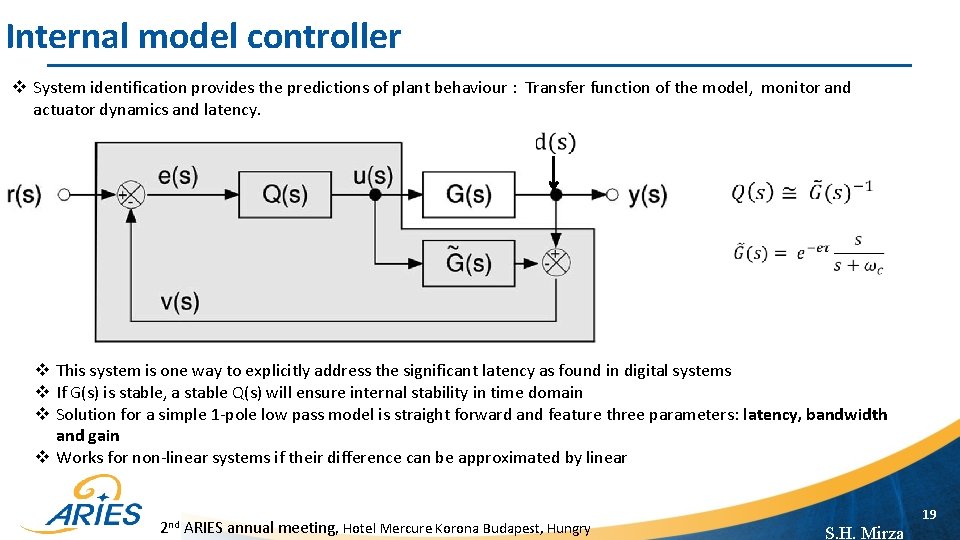
Internal model controller v System identification provides the predictions of plant behaviour : Transfer function of the model, monitor and actuator dynamics and latency. v This system is one way to explicitly address the significant latency as found in digital systems v If G(s) is stable, a stable Q(s) will ensure internal stability in time domain v Solution for a simple 1 -pole low pass model is straight forward and feature three parameters: latency, bandwidth and gain v Works for non-linear systems if their difference can be approximated by linear 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 19 S. H. Mirza

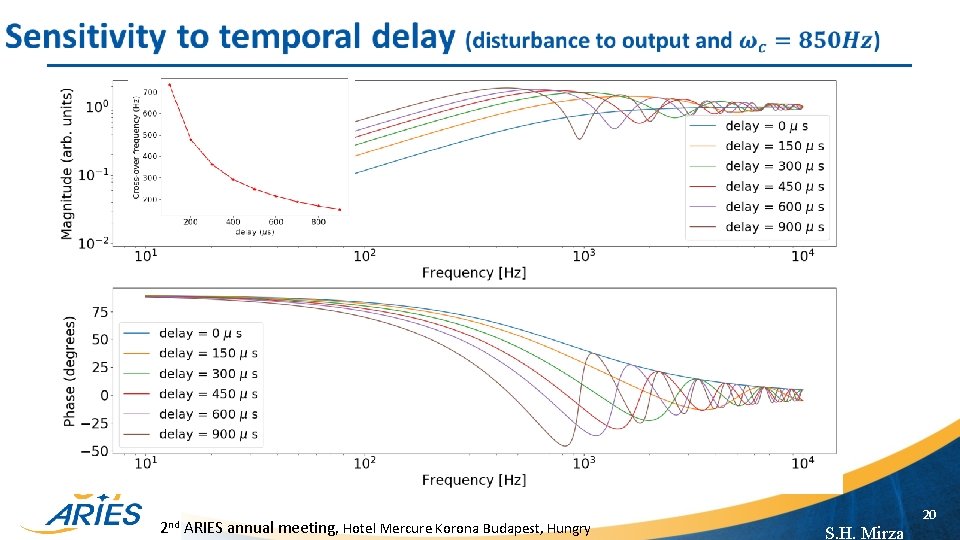
2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 20 S. H. Mirza

Characterizing the effect of spatial model mismatch Corrector settings First iteration residual Focusing magnets defocusing magnets SIS 18 cell Multiple applications triplet focusing magnet nth iteration residual (n costs the bandwidth) Spatial sensitivity function triplet Bending magnets doublet 11/26/202 Correctability No correction Instability 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 21 S. H. Mirza

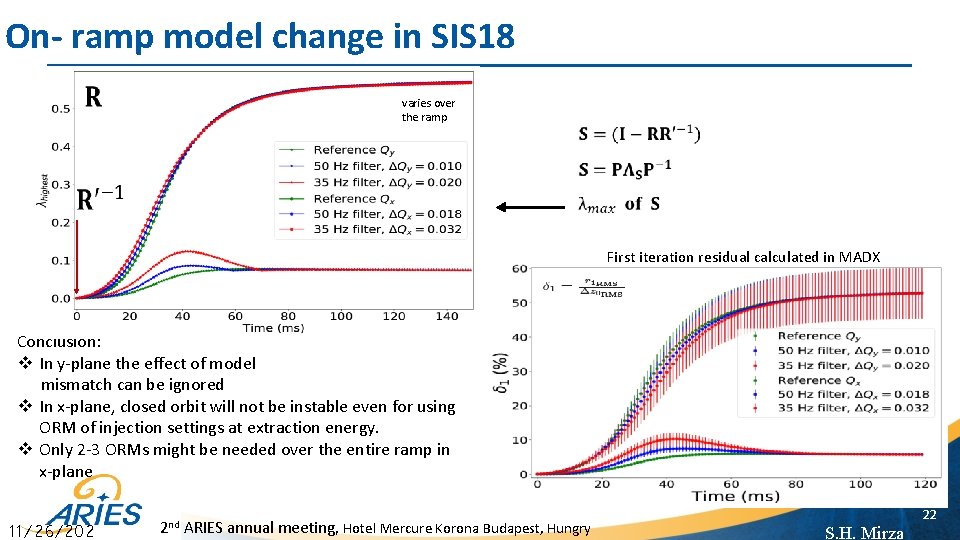
On- ramp model change in SIS 18 varies over the ramp First iteration residual calculated in MADX Conclusion: v In y-plane the effect of model mismatch can be ignored v In x-plane, closed orbit will not be instable even for using ORM of injection settings at extraction energy. v Only 2 -3 ORMs might be needed over the entire ramp in x-plane 11/26/202 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 22 S. H. Mirza

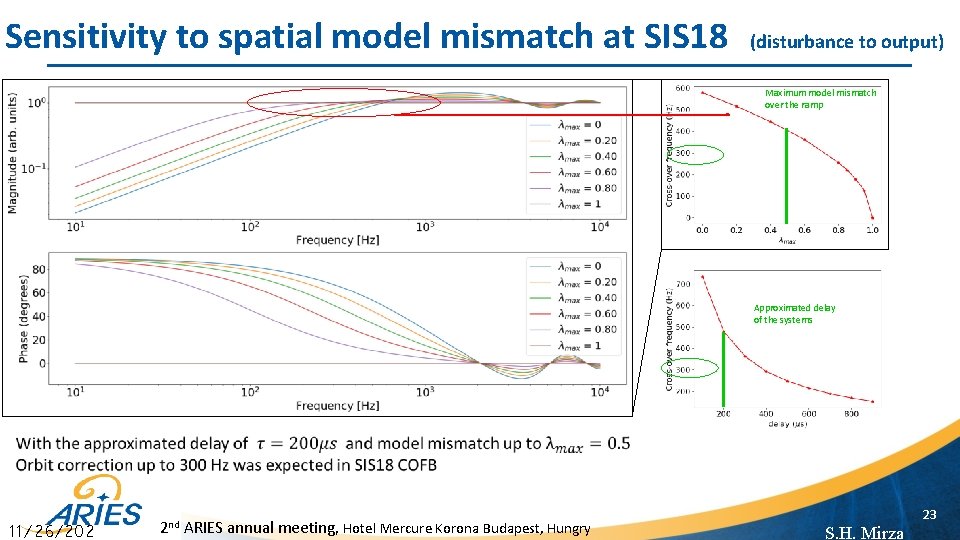
Sensitivity to spatial model mismatch at SIS 18 (disturbance to output) Maximum model mismatch over the ramp Approximated delay of the systems 11/26/202 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 23 S. H. Mirza

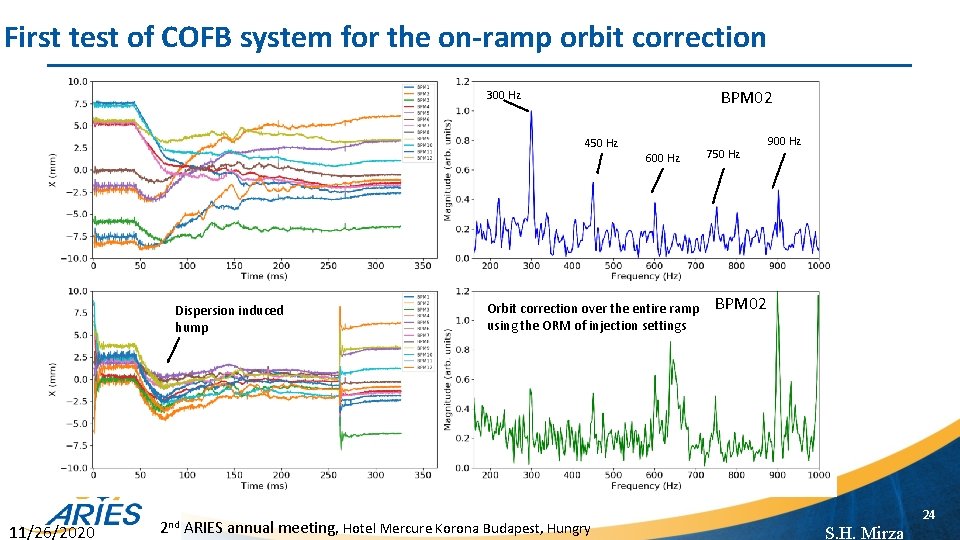
First test of COFB system for the on-ramp orbit correction BPM 02 300 Hz 450 Hz 600 Hz Dispersion induced hump 11/26/2020 Orbit correction over the entire ramp using the ORM of injection settings 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 750 Hz 900 Hz BPM 02 24 S. H. Mirza

Summary v v Closed orbit feedback system has is an integral part of synchrotron operations. Light sources and hadron machines have similarities and differences in requirements. Harmonic analysis and Singular value decomposition are two methods of orbit correction. SVD being more popular. DFT based diagonalization and inversion of the ORM can replace SVD in case of Circulant symmetry and provides more physical interpretation of the mode-space. v Odd position of BPMs and correctors can loss of Circulant symmetry that can be explored by the nearest-Circulant approximation. v Internal model controller design is replacing the classical controllers in COFB design and covers the temporal features like latency, bandwidth and gain more efficiently than classical controller. v The effect of spatial model mismatch is investigated particularly for the on-ramp orbit correction in SIS 18 and is found to decrease the achievable bandwidth of the closed loop. v The first results of the on-ramp orbit correction at SIS 18 synchrotron are presented. Thanks 2 nd ARIES annual meeting, Hotel Mercure Korona Budapest, Hungry 25 S. H. Mirza