State Feedback Controller Design 1 Linear statespace models

State Feedback Controller Design 1. Linear state-space models 2. State feedback control 3. Illustrative example 4. Chemical reactor example 5. Integral state feedback control 6. Simulink example

Linear State-Space Models l Linear deviation model l State-space representation

Open-Loop Stability l State-space matrices l Linear system stability » Steady-state point: » Origin is asymptotically stable if and only if Re[li(A)] < 0 for i = 1, 2, …, n » Origin is unstable if Re[li(A)] > 0 for any i

State Feedback Control l Objectives » Choose eigenvalues of closed-loop system » Decrease response time of open-loop stable system » Stabilize open-loop unstable system l State feedback control law » K is the controller gain matrix » Requires measurement of all state variables

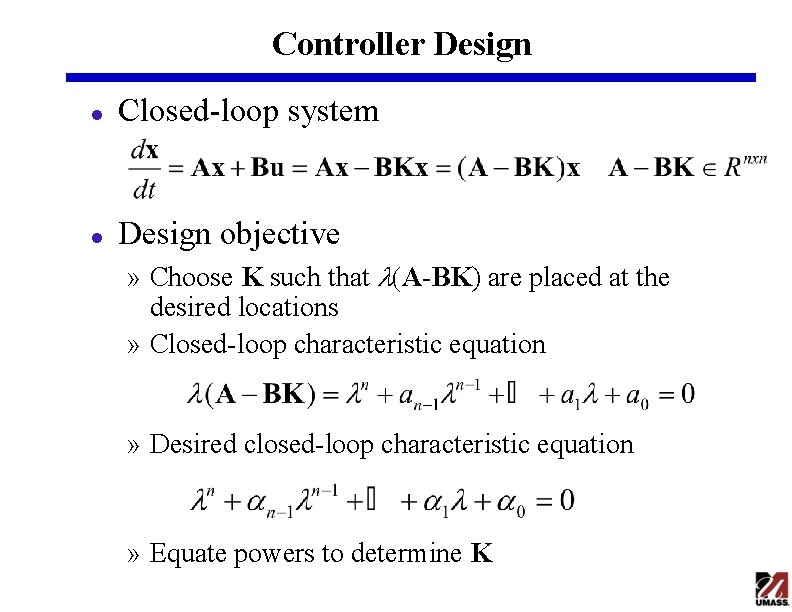
Controller Design l Closed-loop system l Design objective » Choose K such that l(A-BK) are placed at the desired locations » Closed-loop characteristic equation » Desired closed-loop characteristic equation » Equate powers to determine K

Controllability l l Eigenvalues can be placed arbitrarily if and only if (iff) system is controllable Single input (m = 1) » Controllability matrix » System is controllable iff WC is nonsingular l Multiple inputs (m > 1) » Controllability matrix » System is controllable iff rank(WC) = n

Illustrative Example l Linear model l Open-loop stability » li(A) = -0. 438, -4. 56 » Origin is a stable steady state l Controllability

Illustrative Example cont. l Characteristic equation l Desired characteristic equation l Controller gains

Chemical Reactor Example l Process » Continuous stirred tank reactor » Constant volume & cooling jacket temperature » Reaction: A B l Constitutive relations » Reaction kinetics: k(T) = koexp(-E/RT)CA » Heat transfer: Q = UA(Tc-T) l Mass & energy balance equations

Linearized Reactor Model l l Parameter values taken from Bequette (1998) Steady-state: Tc = 25 o. C, CA = 5. 52 kgmol/m 3, T = 339. 1 o. C l Linearized model l Open-loop stability » li(A) = -0. 837, +0. 494 » Steady state is unstable

Reactor State Feedback Control l Controllability » System is controllable l Characteristic equation l Desired characteristic equation l Control law

Integral State Feedback Control l State-space model l Integral state l Augmented state-space model

Integral State Feedback Control cont. l l Design state feedback controller for augmented system Compute controller gains by eigenvalue assignment

Simulink Example >> a=[-1 1; 2 -4]; >> b=[1; 0]; >> rank(wc) ans = 2 >> eig(a) >> p=[-0. 3; -0. 4]; ans = >> k=place(a, b, p) -0. 4384 k= -4. 5616 -4. 3000 >> wc=ctrb(a, b) >> c=[1 0; 0 1]; wc = >> d=[0; 0]; 1 -1 0 2 7. 6600

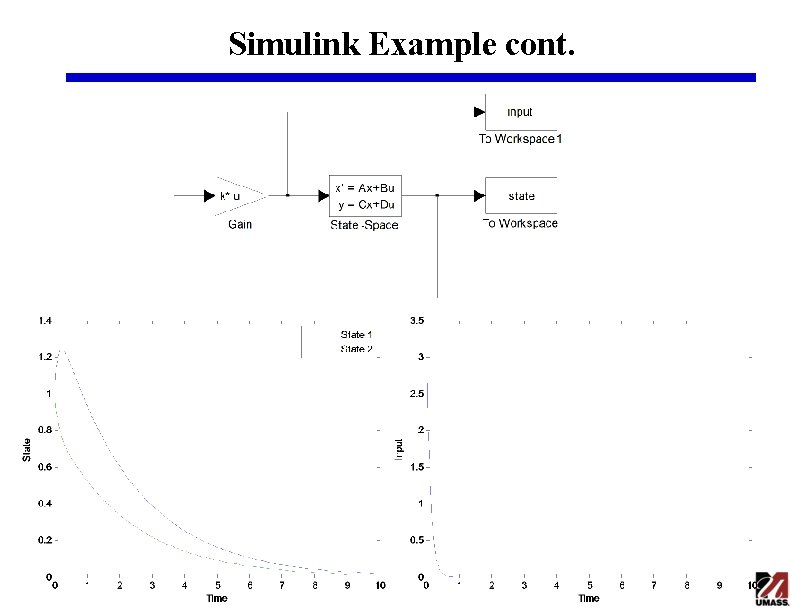
Simulink Example cont.