State complexities of transducers for bidirectional decoding of

State complexities of transducers for bidirectional decoding of prefix codes Laura Giambruno and Sabrina Mantaci Dipartimento di Matematica e Informatica, Università di Palermo.

Outline �Definitions �Girod’s encoding and its generalization �Transducers for Girod’s generalization decoding �Sizes of prefix languages �Results on the number of states �Open problems and Conclusions

Definitions on codes g: B A+ b x If w=b 1…bn then g(w)= g(b 1)…g(bn). g is an encoding if g(w) = g(w′) implies that w = w′. g(B) is said a code (a variable length code) Example: B={b 1, b 2, b 3}. Let g a map from B in A={0, 1}* defined as g(b 1)=10, g(b 2)=001, g(b 3)=010 A decoding is the inverse operation than encoding i. e. the decoding of g is the function g− 1 restricted to g(B∗).

Prefix codes A code X is said prefix (resp. suffix ) if no element of X is a prefix (resp. a suffix) of another element of X. Prefix codes , on an alphabet of cardinality k, are easy to obtain, since they are in correspondence with k-ari trees. Example: X={00, 01, 10}

Prefix codes Remark: A prefix code can be decoded without any delay in a left-to-right parsing while it can not be as easily decoded from right to left. Example: X={10, 001, 010} prefix code. w=00101010010

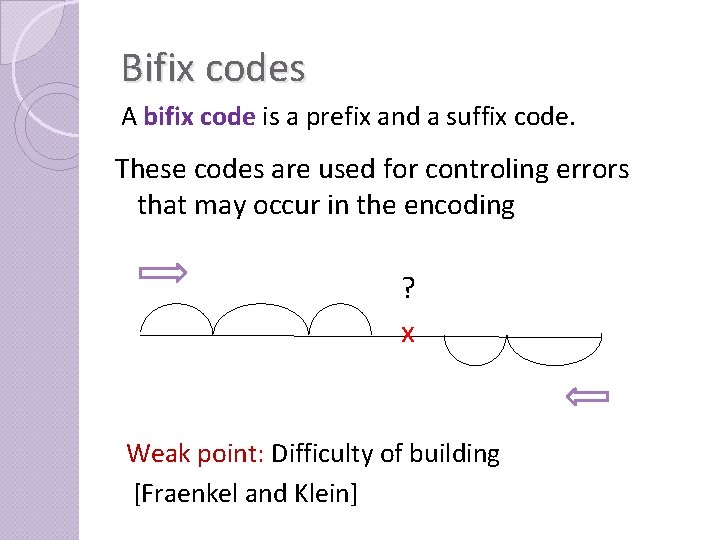
Bifix codes A bifix code is a prefix and a suffix code. These codes are used for controling errors that may occur in the encoding ? x Weak point: Difficulty of building [Fraenkel and Klein]

Girod’s encoding Girod gave a method , where any sequence of codewords in X prefix code is transformed into a bitstring that can be bidirectionally decoded. B. Girod. Bidirectionally decodable streams of prefix code words. IEEE Communications Letters, 1999.

Example Girod’s encoding X={11, 011} y=1101101111 X’={11, 110} y’=1111011011 x = y 000 = 1101101111000 x’= 000 y’ = 0001111011011 z = x x = 1100010100011 where for a, b either both 1 or both 0, a ⊕ b returns 0 and in the other cases it returns 1 z is the Girod’s encoding of w=b 1 b 2 b 2 b 1 where g(b 1)=11 and g(b 2)=011 Remark: z=x x’ implies that x=z x’ and x’=z x

Example Girod’s decoding X={11, 011} z = 1100010100011 x’ = 00011 110110 11 x = 11011011110 00 b 1 b 2 b 1

Generalization of Girod’s encoding • In Girod’s method the decoding key is 0 L, where L is the maximal length of the words of X. • As key one can choose any word of length L. • In particular we can choose the smallest one in the lexicographic order among the words of maximal length in the code.

Transducers Let A, B finite alphabets. A transducer T is a 4 -tuple T = (Q, I, F, E) where - Q is a finite set of states, - I, F Q are sets of initial and final states, - E is the set of 4 -tuples (p, u, v, q) called edges, with p, q in Q, u in A∗, v in B∗ An edge is usually denoted by p u|v q

Transducers We can represent encoding and decoding using transducers: in particular every transducer defines a relation. by A transducer is literal if each input label is a letter. A literal transducer is deterministic (resp. codeterministic) if for each state p and for each input letter a there exists at most an edge that starts (resp. ends) at p with input letter a.

Transducers A sequential transducer is a transducer with a unique initial state i such that the initial state i and the final states have attached each one a word Hence an additional prefix and suffix can be attached to all outputs. There exists a unique minimal sequential transducer equivalent to a given one.

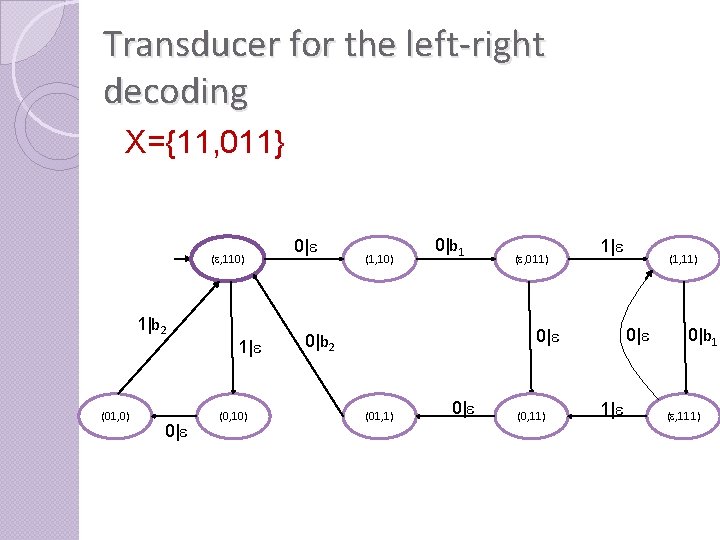
Transducer for the left-right decoding X={11, 011} (e, 110) 1|b 2 (01, 0) 0|e 1|e (0, 10) 0|e (1, 10) 0|b 1 (e, 011) 1|e 0|e 0|b 2 (01, 1) 0|e (0, 11) (1, 11) 1|e 0|b 1 (e, 111)

Properties The transducer for the left-right decoding is : Deterministic Codeterministic Only one Minimal initial and final state

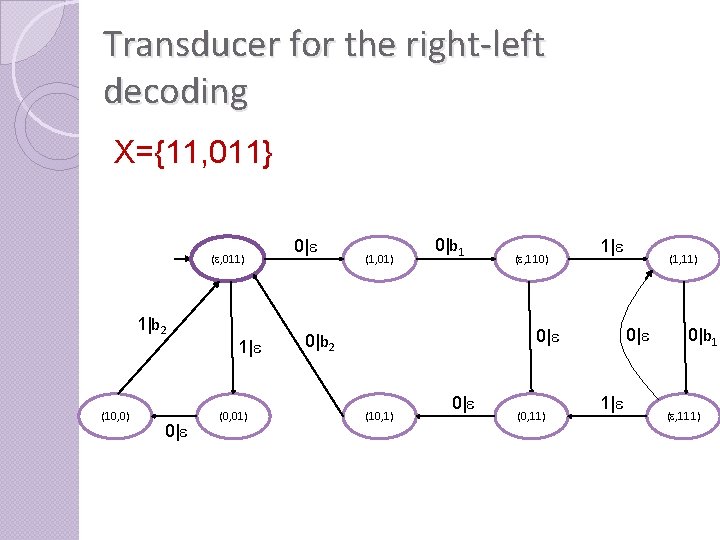
Transducer for the right-left decoding X={11, 011} (e, 011) 1|b 2 (10, 0) 0|e 1|e (0, 01) 0|e (1, 01) 0|b 1 (e, 110) 1|e 0|e 0|b 2 (10, 1) 0|e (0, 11) (1, 11) 1|e 0|b 1 (e, 111)

Isomorphism Theorem: The transducer for the left-right decoding and that one for the right-left decoding are isomorphic. • This depends on the fact that the first transducer decode x from left to right, by knowing bits of x’, the second one decode x’ from right to left, by knowing bits of x.

On the number of states The study of the number of states of transducers associated to these decoding is interesting for an algorithmic point of view. Let X = {x 1, x 2, . . . , xm} be a prefix code a binary alphabet. We can measure the size of X in different ways: the cardinality of X the sum of the lengths of the elements in X the size of the binary tree TX naturally associated to X, i. e. the number of its nodes L = maxx∈X |x|, the length of the longest word in X.

On the number of states: general results X prefix code TX =(Q, i, i, E) associated transducer We have the following general upper bound: Theorem: If X is a prefix code then |Q| ≤ L 2 L The number of states of the transducer grows when adding words to the prefix code: Lemma: Let Y ⊆ X be prefix codes such that the length of the longest word in X is the length of the longest word in Y. Then Ty is contained in TX and the number of states of Ty is strictly less than the number of states of TX

Maximal prefix codes are codes such that no word can be added in order to have still a prefix code. Maximal prefix codes are represented by complete trees, i. e. trees where each node has two or zero subtrees. Example: X={000, 001, 010, 011, 10, 11} Example: X={00, 01, 10}

Maximal prefix codes For maximal prefix codes we get an exact formula that computes the number of states of the associated transducer: Lemma: If X is a maximal prefix code then, for each pair of words (u, v) with u prefix of X and v ∈ AL−|u|, we have that (u, v) ∈ Q. Prefi(X) set of prefixes of length i of the words in X Leveli(X) set of nodes in the tree TX of level i

Maximal prefix codes: exact formula and lower bound Theorem: If X is a maximal prefix code then, We can deduce an exponential lower bound in L for maximal prefix codes: Corollary: If X is a maximal prefix code then

Uniform codes A prefix code X is uniform if all the words in X have the same length L. A maximal uniform code whose words have length L contains all the words of this length. Theorem: If X is a uniform maximal code then

Uniform maximal codes Let X be a uniform maximal prefix code. Since , and the number of states of TX is equal to , Linear dependence on the length of X. Polynomial dependence on the size of the tree TX

String-codes Let u be a word in A = {0, 1}. We define Xu the string-code of u as Xu ={u} ∪ {va | vā ∈ Pref(u)}, where ā is the bit opposite to a Example: Xu , with u=01001

String-codes Theorem: If Xu is a string-code then Let X be a string-code. Since and we have that , Exponential dependences on the different sizes of X.

Uniform codes For uniform codes of two words we have a precise result for the state complexity: if In general Proposition: If X is a non maximal uniform code then. This bound is tight for codes of two words beginning with different letters. Upper bound for the number of states of for non maximal prefix codes.

Isomorphic codes Given two binary trees T 1 and T 2, we say that they are isomorphic if T 2 can be obtained from T 1 by choosing some of its nodes and, for each of them switching the right and the left subtree. Two prefix codes are isomorphic if the associated trees are isomorphic. Example:

Isomorphic codes By experimental results, we see that if X 1 and X 2 are two isomorphic prefix codes, then the corresponding transducers have the same number of states. We conjecture that this is a general property and that the corresponding transducers are isomorphic as unlabeled graphs. Proposition: Transducer associated to isomorphic string-codes have the same number of states.

Open problems Finding upper bound for the growing of the number of states of the transducer associated to a prefix code X, when adding another word to X. Finding general upper and lower bound depending on the size of the tree. Average studies on the number of states for different distribution on prefix codes.

Thank you! Merci beaucoup!