STAT 101 Dr Kari Lock Morgan Normal Distribution

STAT 101 Dr. Kari Lock Morgan Normal Distribution Chapter 5 • Normal distribution • Central limit theorem • Normal distribution for confidence intervals • Normal distribution for p-values • Standard normal Statistics: Unlocking the Power of Data Lock 5

Re-grade Requests � 4 e potential grading mistake: 0. 025 is correct �Requests for a re-grade must be submitted in writing by class on Wednesday, March 5 th �Partial credit will NOT be adjusted �Valid re-grade requests: You got points off but believe your answer is correct Points were added incorrectly �Warning: scores may go up or down Statistics: Unlocking the Power of Data Lock 5
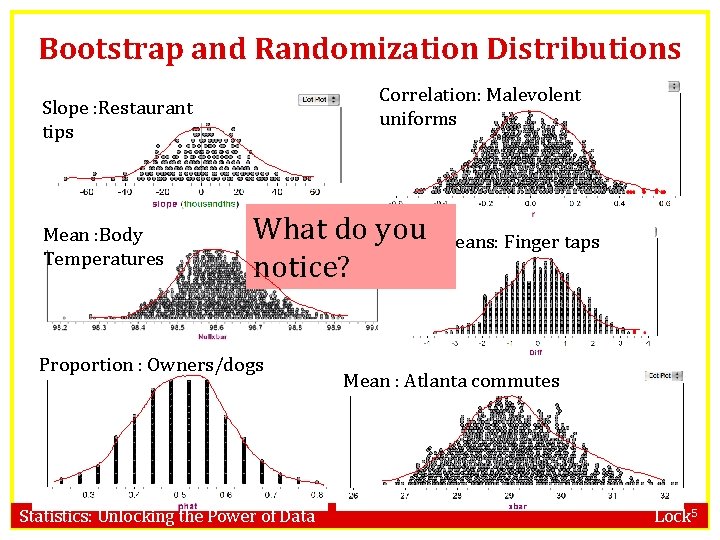
Bootstrap and Randomization Distributions Correlation: Malevolent uniforms Slope : Restaurant tips Mean : Body Temperatures What do you Diff means: Finger taps notice? Proportion : Owners/dogs Statistics: Unlocking the Power of Data Mean : Atlanta commutes Lock 5
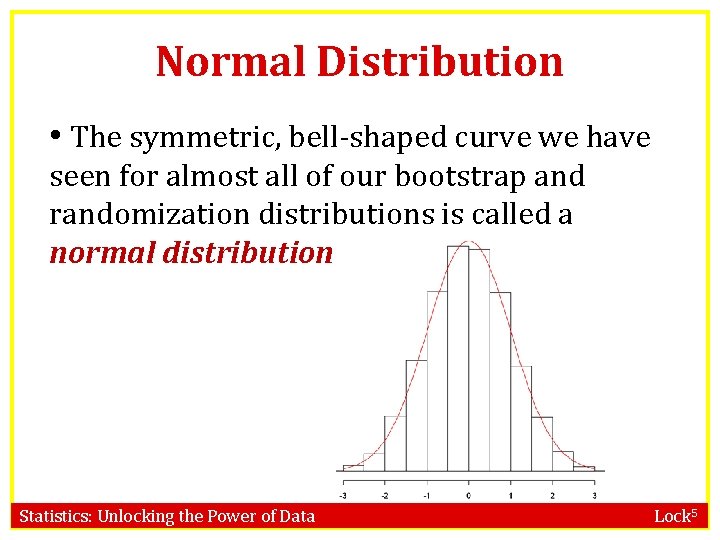
Normal Distribution • The symmetric, bell-shaped curve we have seen for almost all of our bootstrap and randomization distributions is called a normal distribution Statistics: Unlocking the Power of Data Lock 5

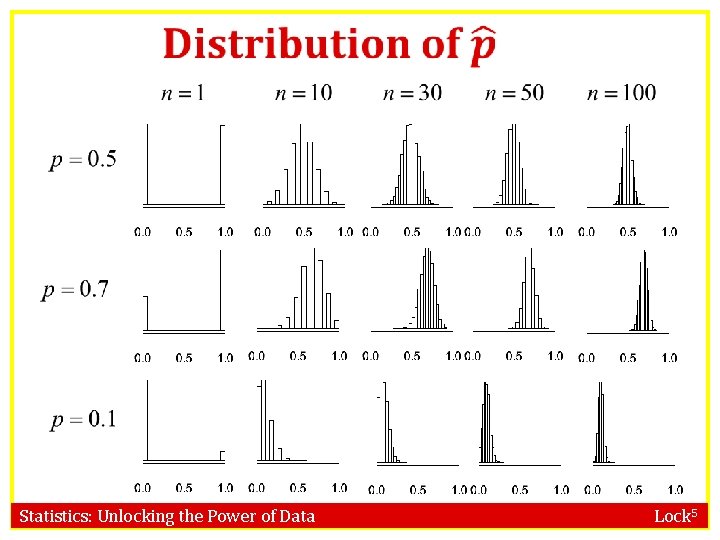
Central Limit Theorem! For a sufficiently large sample size, the distribution of sample statistics for a mean or a proportion is normal www. lock 5 stat. com/Stat. Key Statistics: Unlocking the Power of Data Lock 5
Statistics: Unlocking the Power of Data Lock 5
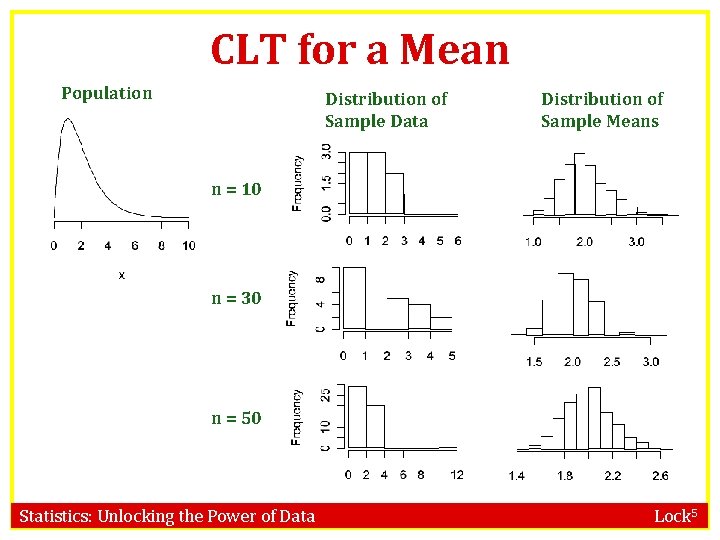
CLT for a Mean Population Distribution of Sample Data Distribution of Sample Means n = 10 n = 30 n = 50 Statistics: Unlocking the Power of Data Lock 5

Central Limit Theorem • The central limit theorem holds for ANY original distribution, although “sufficiently large sample size” varies • The more skewed the original distribution is (the farther from normal), the larger the sample size has to be for the CLT to work • For small samples, it is more important that the data itself is approximately normal Statistics: Unlocking the Power of Data Lock 5

Central Limit Theorem • For distributions of a quantitative variable that are not very skewed and without large outliers, n ≥ 30 is usually sufficient to use the CLT • For distributions of a categorical variable, counts of at least 10 within each category is usually sufficient to use the CLT Statistics: Unlocking the Power of Data Lock 5

Accuracy • The accuracy of intervals and p-values generated using simulation methods (bootstrapping and randomization) depends on the number of simulations (more simulations = more accurate) • The accuracy of intervals and p-values generated using formulas and the normal distribution depends on the sample size (larger sample size = more accurate) • If the distribution of the statistic is truly normal and you have generated many simulated randomizations, the p-values should be very close Statistics: Unlocking the Power of Data Lock 5

Normal Distribution • The normal distribution is fully characterized by it’s mean and standard deviation Statistics: Unlocking the Power of Data Lock 5

Bootstrap Distributions If a bootstrap distribution is approximately normally distributed, we can write it as a) b) c) d) N(parameter, sd) N(statistic, sd) N(parameter, se) N(statistic, se) sd = standard deviation of variable se = standard error = standard deviation of statistic Statistics: Unlocking the Power of Data Lock 5

Hearing Loss • In a random sample of 1771 Americans aged 12 to 19, 19. 5% had some hearing loss (this is a dramatic increase from a decade ago!) • What proportion of Americans aged 12 to 19 have some hearing loss? Give a 95% CI. Rabin, R. “Childhood: Hearing Loss Grows Among Teenagers, ” www. nytimes. com, 8/23/10. Statistics: Unlocking the Power of Data Lock 5
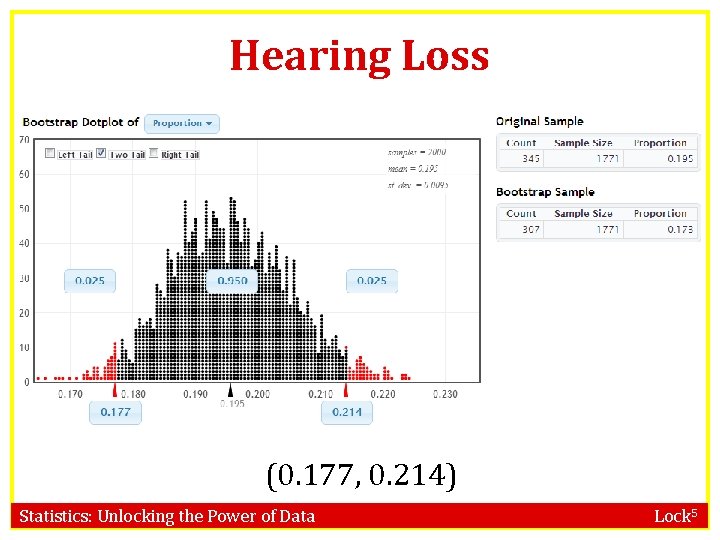
Hearing Loss (0. 177, 0. 214) Statistics: Unlocking the Power of Data Lock 5
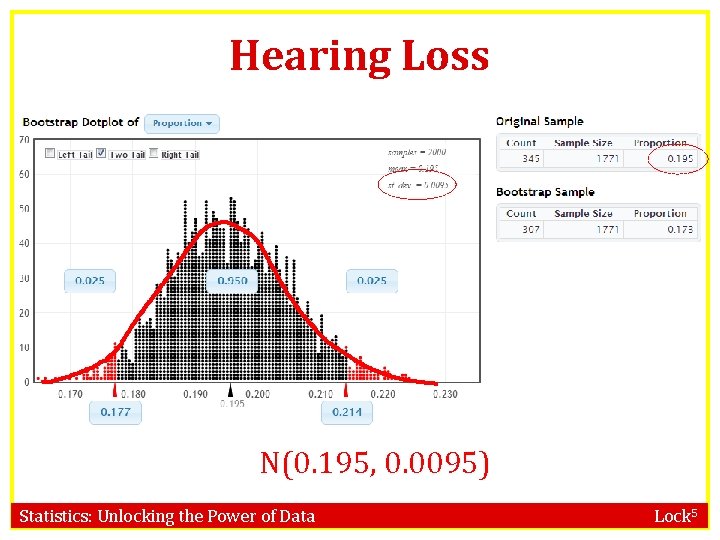
Hearing Loss N(0. 195, 0. 0095) Statistics: Unlocking the Power of Data Lock 5

Confidence Intervals If the bootstrap distribution is normal: To find a P% confidence interval , we just need to find the middle P% of the distribution N(statistic, SE) Statistics: Unlocking the Power of Data Lock 5

Area under a Curve • The area under the curve of a normal distribution is equal to the proportion of the distribution falling within that range • Knowing just the mean and standard deviation of a normal distribution allows you to calculate areas in the tails and percentiles www. lock 5 stat. com/statkey Statistics: Unlocking the Power of Data Lock 5
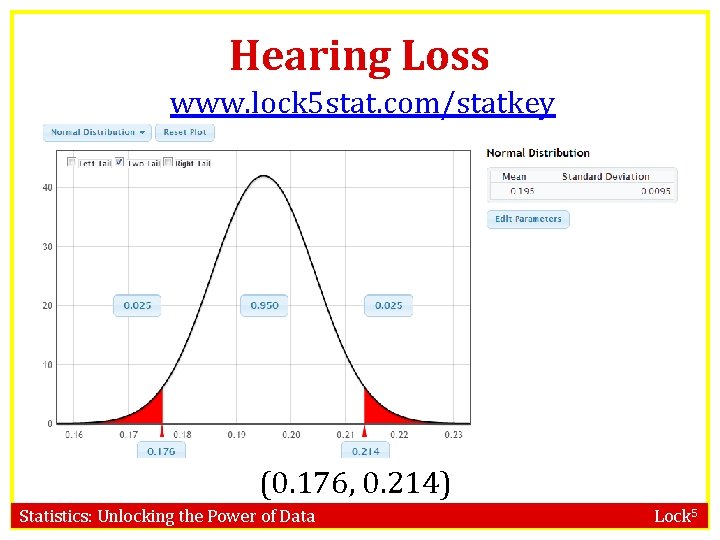
Hearing Loss www. lock 5 stat. com/statkey (0. 176, 0. 214) Statistics: Unlocking the Power of Data Lock 5

Standardized Data �Often, we standardize the data to have mean 0 and standard deviation 1 �This is done with z-scores From x to z : From z to x: �Places everything on a common scale Statistics: Unlocking the Power of Data Lock 5
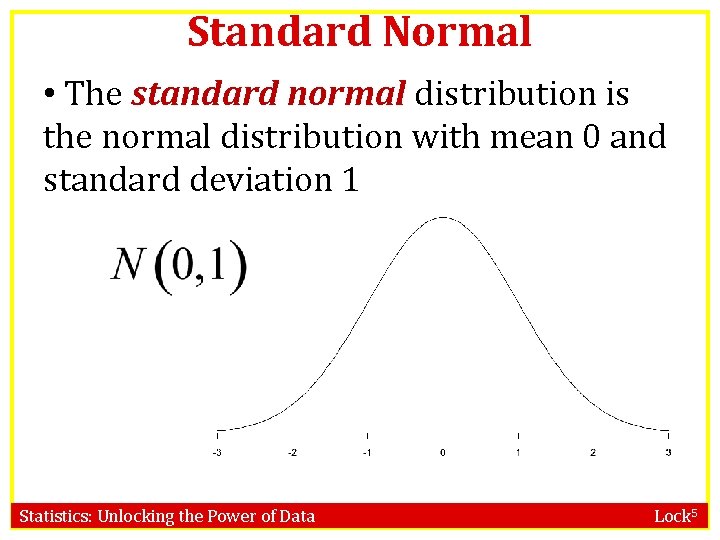
Standard Normal • The standard normal distribution is the normal distribution with mean 0 and standard deviation 1 Statistics: Unlocking the Power of Data Lock 5

Standardized Data �Confidence Interval (bootstrap distribution): mean = sample statistic, sd = SE From z to x: (CI) Statistics: Unlocking the Power of Data Lock 5
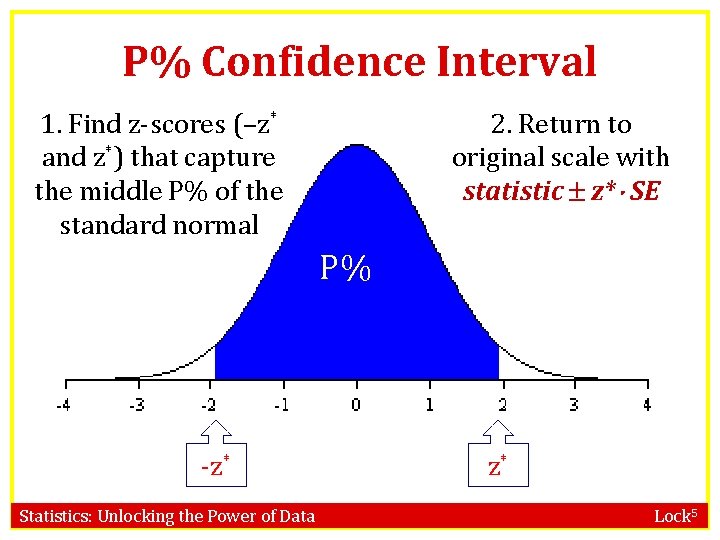
P% Confidence Interval 1. Find z-scores (–z* and z*) that capture the middle P% of the standard normal 2. Return to original scale with statistic z* SE P% -z* Statistics: Unlocking the Power of Data z* Lock 5

Confidence Interval using N(0, 1) If a statistic is normally distributed, we find a confidence interval for the parameter using statistic z* SE where the area between –z* and +z* in the standard normal distribution is the desired level of confidence. Statistics: Unlocking the Power of Data Lock 5

Confidence Intervals Find z* for a 99% confidence interval. www. lock 5 stat. com/statkey z* = 2. 575 Statistics: Unlocking the Power of Data Lock 5

z* �Why use the standard normal? �Common confidence levels: 95%: z* = 1. 96 (but 2 is close enough) 90%: z* = 1. 645 99%: z* = 2. 576 Statistics: Unlocking the Power of Data Lock 5

Sin Taxes In March 2011, a random sample of 1000 US adults were asked “Do you favor or oppose ‘sin taxes’ on soda and junk food? ” 320 adults responded in favor of sin taxes. Give a 99% CI for the proportion of all US adults that favor these sin taxes. From a bootstrap distribution, we find SE = 0. 015 Statistics: Unlocking the Power of Data Lock 5

Sin Taxes Statistics: Unlocking the Power of Data Lock 5
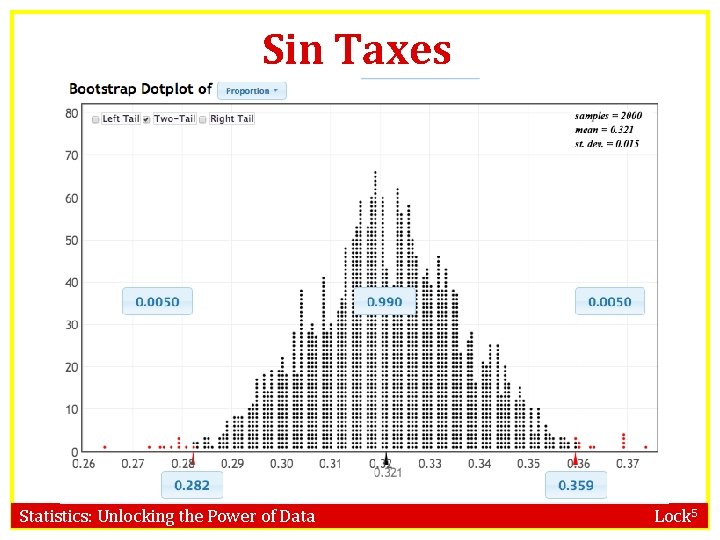
Sin Taxes Statistics: Unlocking the Power of Data Lock 5

Randomization Distributions If a randomization distribution is approximately normally distributed, we can write it as a) N(null value, se) b) N(statistic, se) c) N(parameter, se) Statistics: Unlocking the Power of Data Lock 5

p-values If the randomization distribution is normal: To calculate a p-value, we just need to find the area in the appropriate tail(s) beyond the observed statistic of the distribution Statistics: Unlocking the Power of Data Lock 5

First Born Children Statistics: Unlocking the Power of Data Lock 5

First Born Children Statistics: Unlocking the Power of Data Lock 5
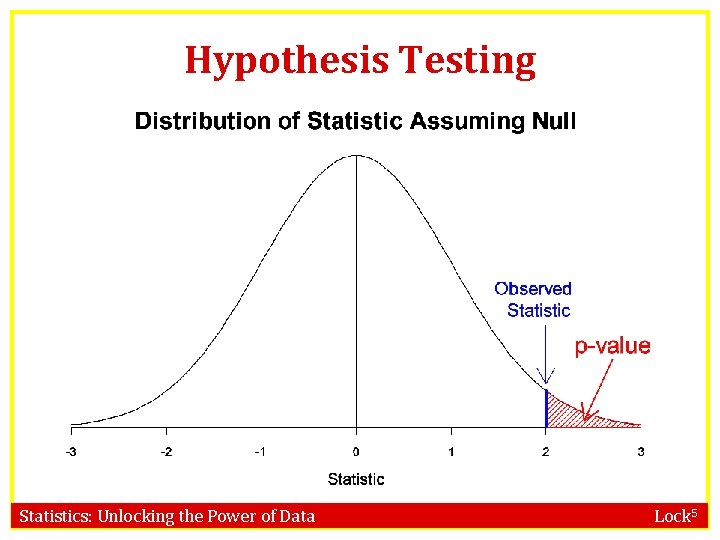
Hypothesis Testing Statistics: Unlocking the Power of Data Lock 5
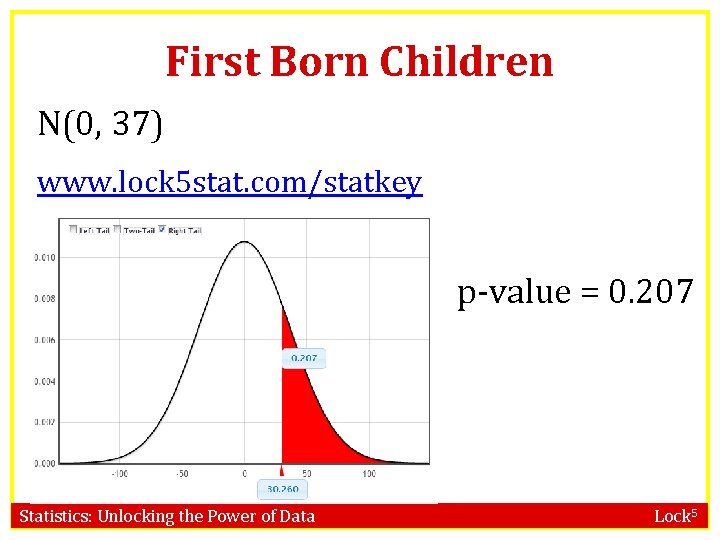
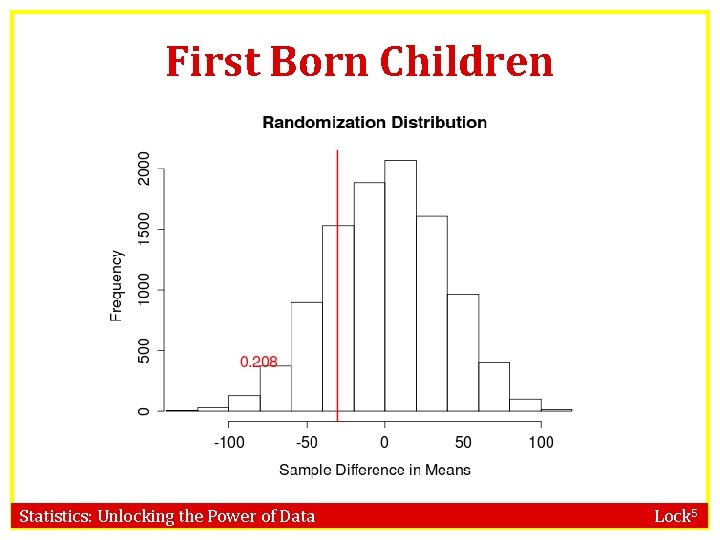
First Born Children N(0, 37) www. lock 5 stat. com/statkey p-value = 0. 207 Statistics: Unlocking the Power of Data Lock 5

Standardized Data �Hypothesis test (randomization distribution): mean = null value, sd = SE From x to z (test) : Statistics: Unlocking the Power of Data Lock 5

p-value using N(0, 1) Statistics: Unlocking the Power of Data Lock 5

First Born Children Statistics: Unlocking the Power of Data Lock 5
First Born Children Statistics: Unlocking the Power of Data Lock 5

z-statistic If z = – 3, using = 0. 05 we would (a) Reject the null (b) Not reject the null (c) Impossible to tell (d) I have no idea Statistics: Unlocking the Power of Data Lock 5

z-statistic • Calculating the number of standard errors a statistic is from the null value allows us to assess extremity on a common scale Statistics: Unlocking the Power of Data Lock 5

Confidence Interval Formula IF SAMPLE SIZES ARE LARGE… From N(0, 1) From original data Statistics: Unlocking the Power of Data From bootstrap distribution Lock 5

Formula for p-values IF SAMPLE SIZES ARE LARGE… From original data From randomization distribution Statistics: Unlocking the Power of Data From H 0 Compare z to N(0, 1) for p-value Lock 5

Standard Error • Wouldn’t it be nice if we could compute the standard error without doing thousands of simulations? • We can!!! • Or at least we’ll be able to next class… Statistics: Unlocking the Power of Data Lock 5

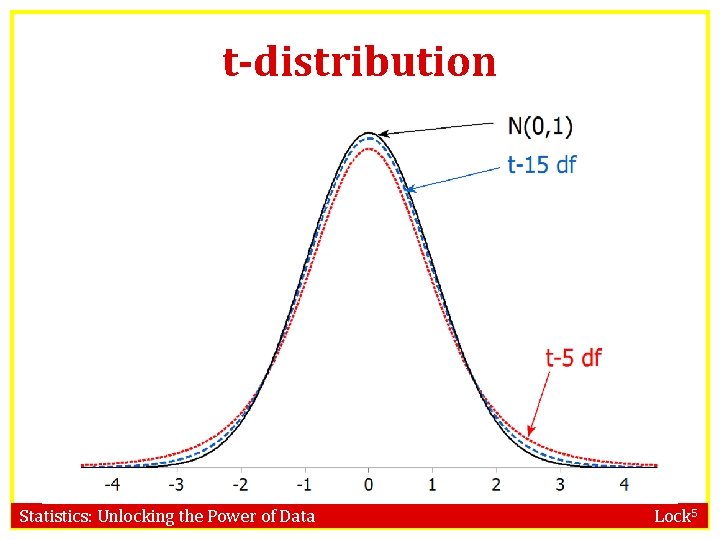
t-distribution • For quantitative data, we use a tdistribution instead of the normal distribution • The t distribution is very similar to the standard normal, but with slightly fatter tails (to reflect the uncertainty in the sample standard deviations) Statistics: Unlocking the Power of Data Lock 5

Degrees of Freedom • The t-distribution is characterized by its degrees of freedom (df) • Degrees of freedom are based on sample size • Single mean: df = n – 1 • Difference in means: df = min(n 1, n 2) – 1 • Correlation: df = n – 2 • The higher the degrees of freedom, the closer the t-distribution is to the standard normal Statistics: Unlocking the Power of Data Lock 5
t-distribution Statistics: Unlocking the Power of Data Lock 5

Aside: William Sealy Gosset Statistics: Unlocking the Power of Data Lock 5

The Pygmalion Effect Teachers were told that certain children (chosen randomly) were expected to be intellectual “growth spurters, ” based on the Harvard Test of Inflected Acquisition (a test that didn’t actually exist). These children were selected randomly. The response variable is change in IQ over the course of one year. Source: Rosenthal, R. and Jacobsen, L. (1968). “Pygmalion in the Classroom: Teacher Expectation and Pupils’ Intellectual Development. ” Holt, Rinehart and Winston, Inc. Statistics: Unlocking the Power of Data Lock 5

The Pygmalion Effect Control Students “Growth Spurters” n 255 65 8. 42 12. 22 s 12. 0 13. 3 Can this provide evidence that merely expecting a child to do well actually causes the child to do better? If so, how much better? SE = 1. 8 *s 1 and s 2 were not given, so I set them to give the correct p-value Statistics: Unlocking the Power of Data Lock 5

Pygmalion Effect Statistics: Unlocking the Power of Data Lock 5
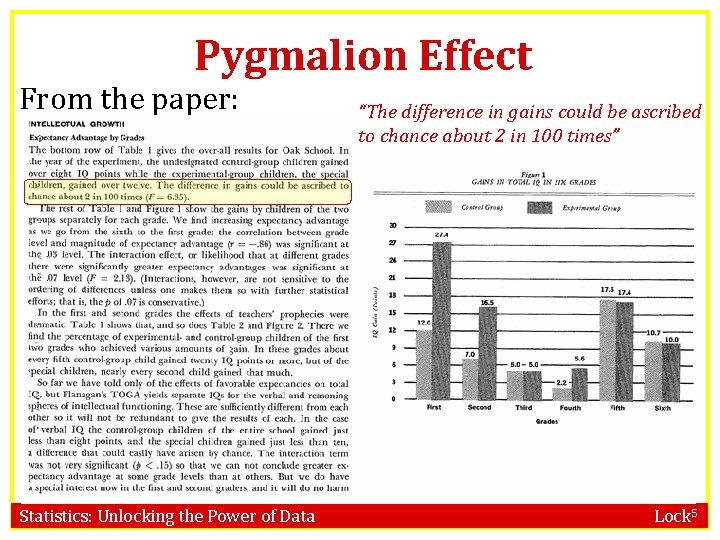
Pygmalion Effect From the paper: Statistics: Unlocking the Power of Data “The difference in gains could be ascribed to chance about 2 in 100 times” Lock 5

Pygmalion Effect Statistics: Unlocking the Power of Data Lock 5

To Do �Do Project 1 (due 3/7) �Read Chapter 5 Statistics: Unlocking the Power of Data Lock 5
- Slides: 53