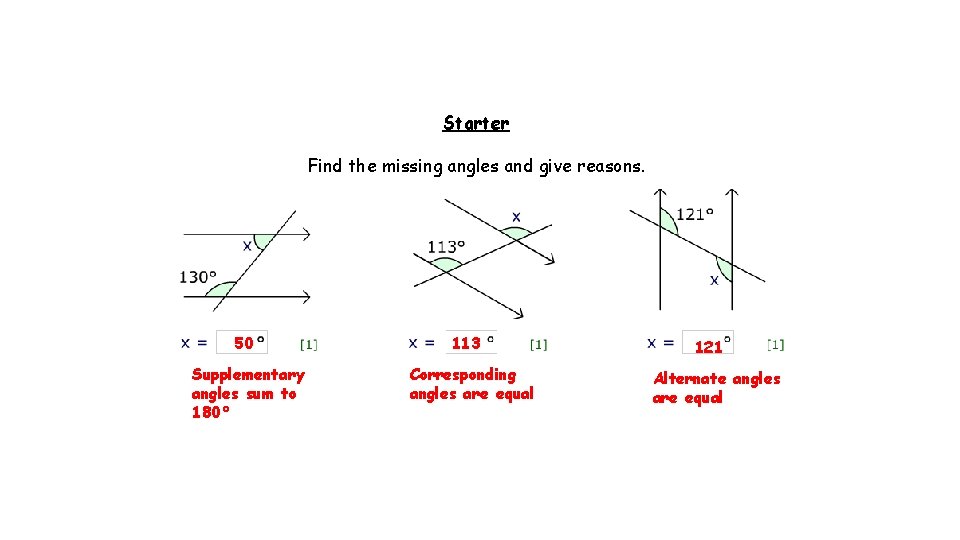
Starter Find the missing angles and give reasons

Circle Theorems Label the diagrams using the key words: Radius Circumference Diameter Arc Centre

Investigation 1) Draw a line from the centre of your circle to a point

Theorem A tangent is perpendicular to a radius.

Investigation 1) Draw two lines from the centre to the circumference. 3) Draw two

Theorem The angle at the centre is twice the angle at the circumference.

Proof = (180 – x)/2 = (180 – y)/2 = 180 – (½x +

Investigation 1) Draw the circle’s diameter. 2) Draw two lines to a point at

Theorem The angle in a semi-circle is 90 o.

Proof = 180° as it is a straight line. Using “the angle at the

Investigation d 1) On your circle pick 4 points a, b, c, d. Don’t

Theorem d c Angles subtended by the same arc are equal. b a

Proof Using “the angle at the centre is twice the angle at the circumference”

Investigation 1) Draw a quadrilateral inside your circle. Every vertex must be touching the

Theorem Opposite angles in a cyclic quadrilateral sum to 180 o.

Investigation 1) Draw a triangle inside your circle with all vertices on the circumference.

Theorem Angles in alternate segments are equal.

Proof For cases when the chord isn’t a diameter? x° 90 -x x° Using

Investigation 1) Draw two tangents from your circle that meet at a point. 2)

Theorem Tangents from a point are equal.

Proof Using Pythagoras’ Theorem r ∴ tangents from a point are equal. x r

Show me a problem that can be solved using: • Angle at the centre

Answers 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 67º

Slides: 26

Download presentation

Starter Find the missing angles and give reasons. 50 Supplementary angles sum to 180° 113 Corresponding angles are equal 121 Alternate angles are equal

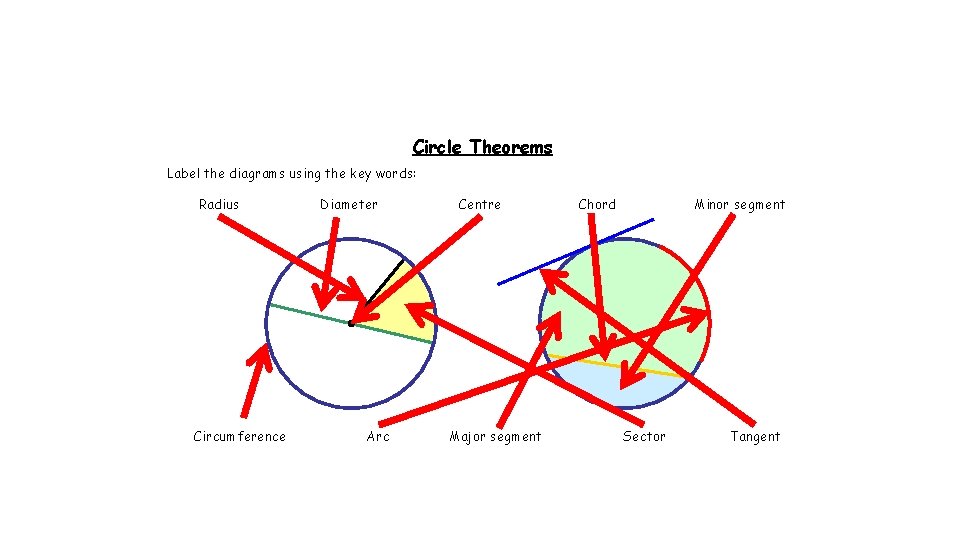
Circle Theorems Label the diagrams using the key words: Radius Circumference Diameter Arc Centre Major segment Chord Minor segment Sector Tangent

Investigation 1) Draw a line from the centre of your circle to a point on the circumference. 2) Draw the tangent at that point. 3) Measure the angle between the radius and the tangent. What can you tell me?

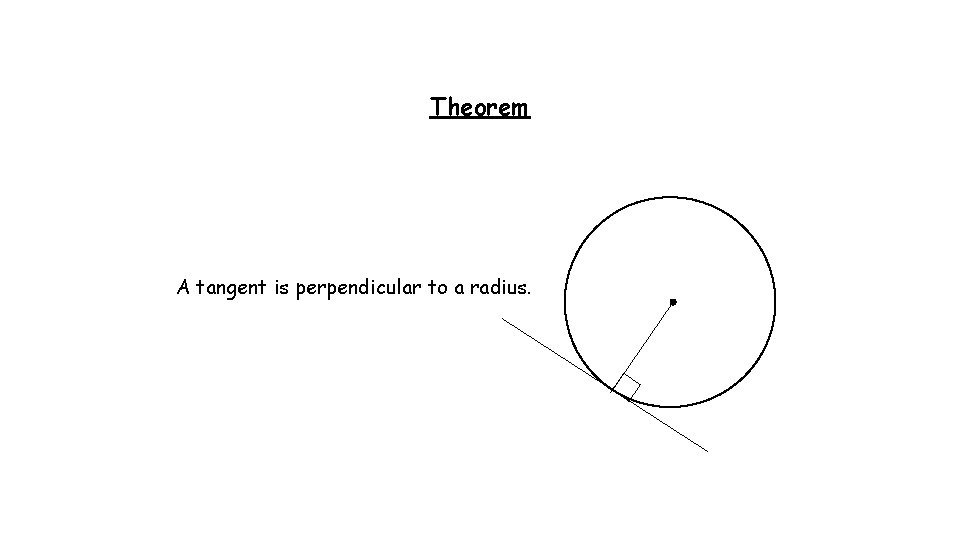
Theorem A tangent is perpendicular to a radius.

Investigation 1) Draw two lines from the centre to the circumference. 3) Draw two more lines to the other side of your circle from the same points that you drew the first two lines. What do you notice?

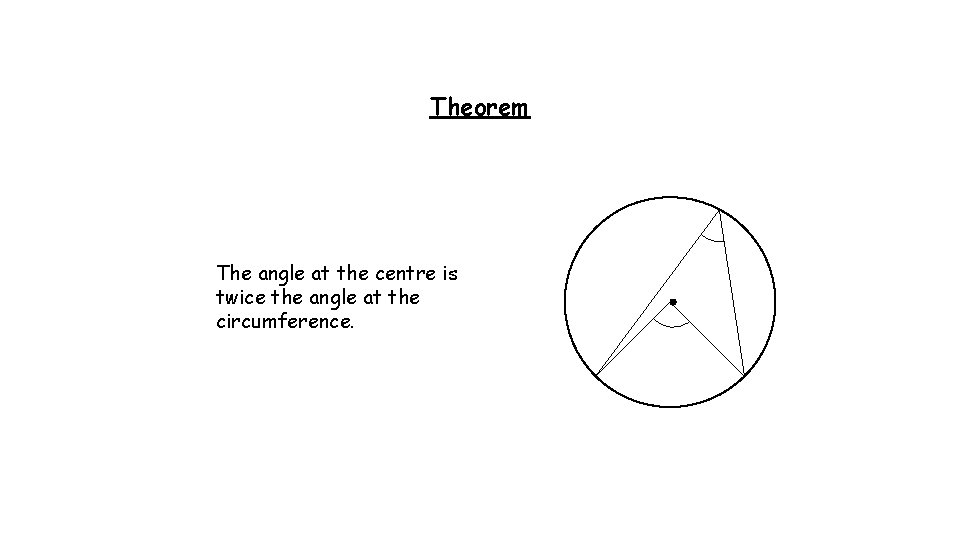
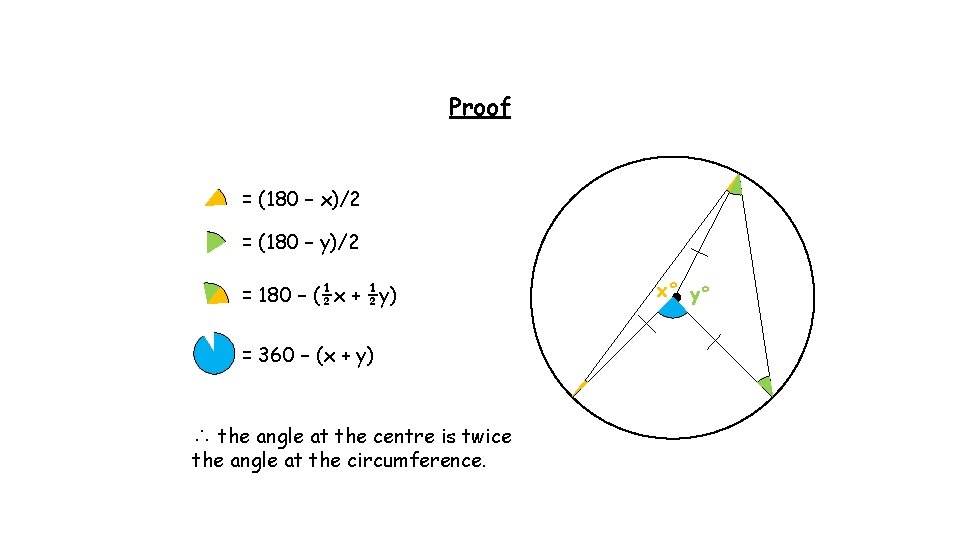
Theorem The angle at the centre is twice the angle at the circumference.

Proof = (180 – x)/2 = (180 – y)/2 = 180 – (½x + ½y) = 360 – (x + y) ∴ the angle at the centre is twice the angle at the circumference. x° y°

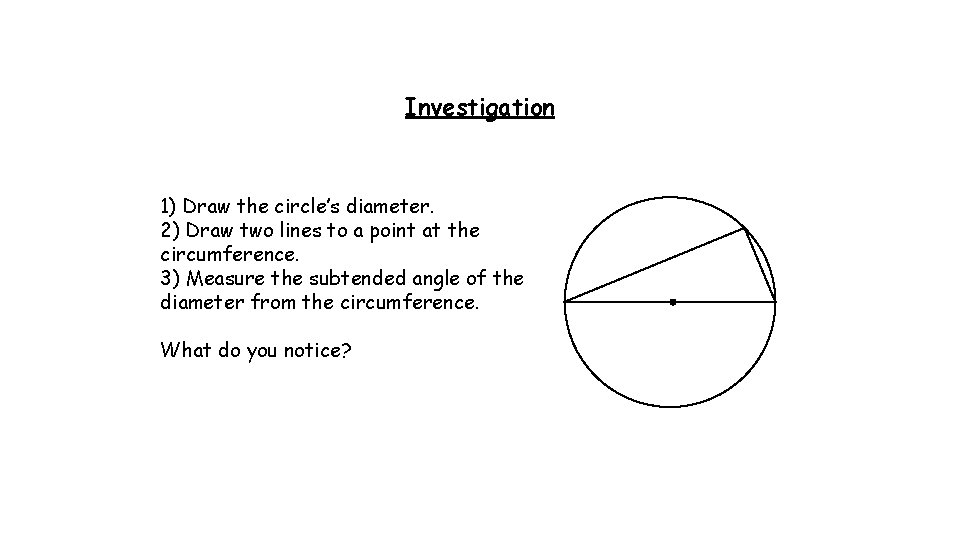
Investigation 1) Draw the circle’s diameter. 2) Draw two lines to a point at the circumference. 3) Measure the subtended angle of the diameter from the circumference. What do you notice?

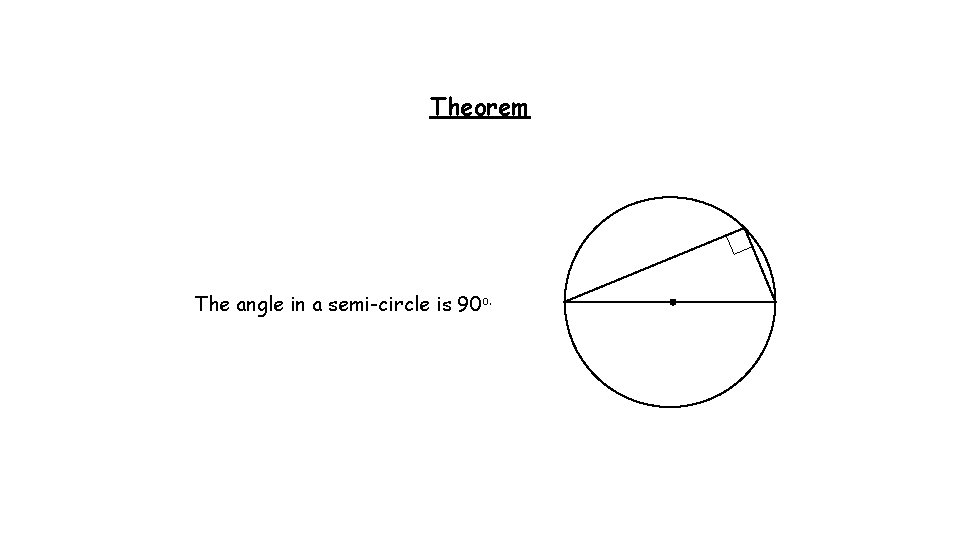
Theorem The angle in a semi-circle is 90 o.

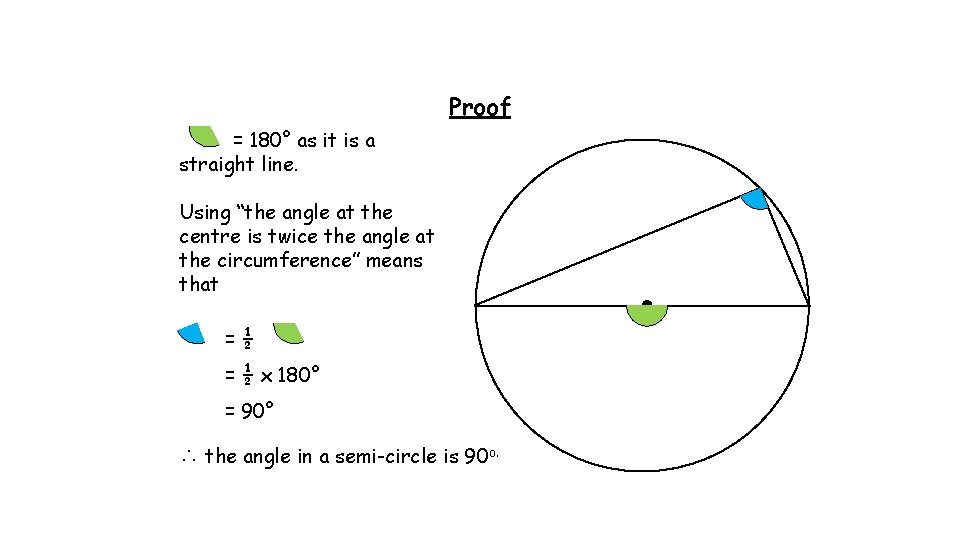
Proof = 180° as it is a straight line. Using “the angle at the centre is twice the angle at the circumference” means that =½ = ½ x 180° = 90° ∴ the angle in a semi-circle is 90 o.

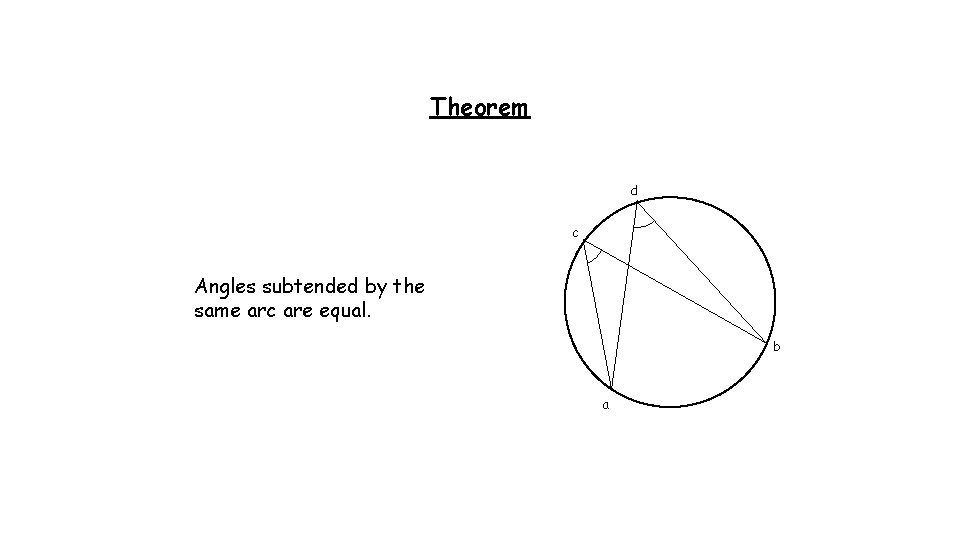
Investigation d 1) On your circle pick 4 points a, b, c, d. Don’t pick points directly opposite each other. 2) Connect points a and b to c. 3) Connect points a and b to d. 4) Measure the angles subtended from a and b at c and d. What do you notice? c b a

Theorem d c Angles subtended by the same arc are equal. b a

Proof Using “the angle at the centre is twice the angle at the circumference” means that =2 x° y° =2 2 x = 2 y ∴ x = y ∴ angles subtended by the same arc are equal. 2 x° 2 y°

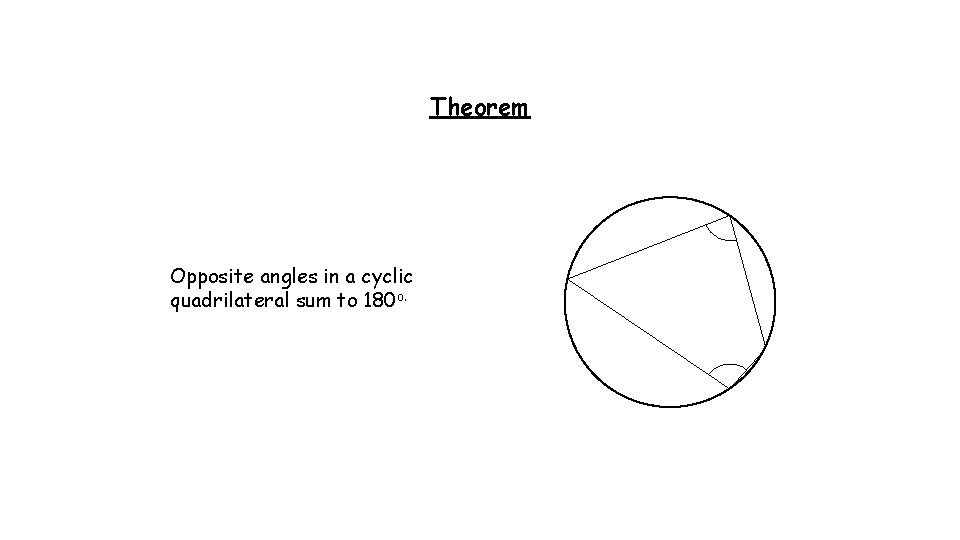
Investigation 1) Draw a quadrilateral inside your circle. Every vertex must be touching the circumference of the circle. 2) Measure the angles inside the quadrilateral. What can you tell me? (Of course they add up to 360; it’s a quadrilateral!)

Theorem Opposite angles in a cyclic quadrilateral sum to 180 o.

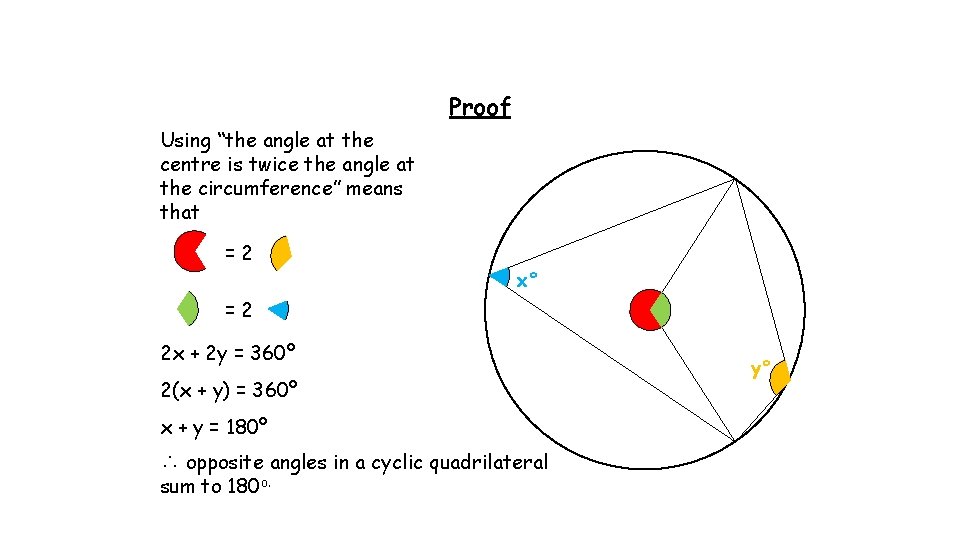
Proof Using “the angle at the centre is twice the angle at the circumference” means that =2 x° =2 2 x + 2 y = 360º 2(x + y) = 360º x + y = 180º ∴ opposite angles in a cyclic quadrilateral sum to 180 o. y°

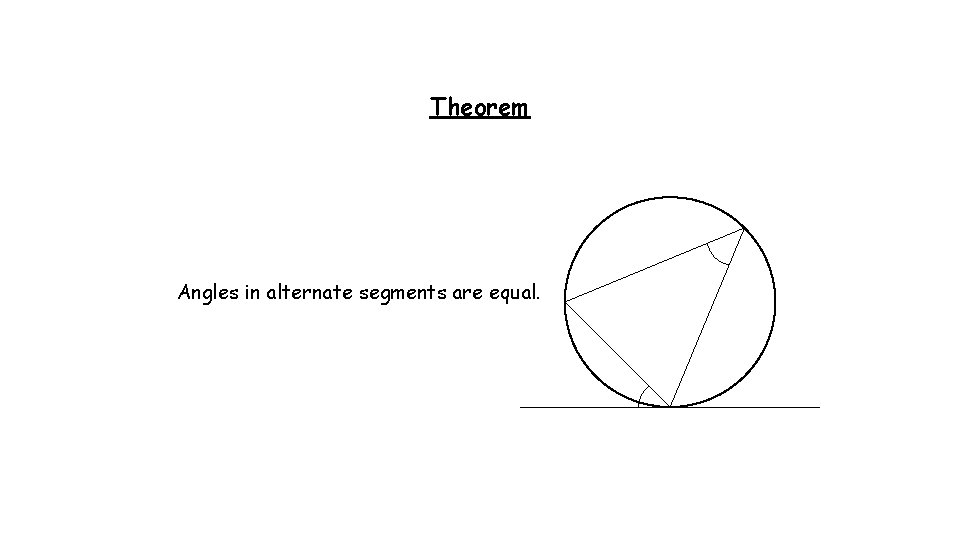
Investigation 1) Draw a triangle inside your circle with all vertices on the circumference. 2) Draw a tangent at one of the vertices. 3) Measure the angles between the tangent and the triangle, and the angles of the triangle. What can you tell me?

Theorem Angles in alternate segments are equal.

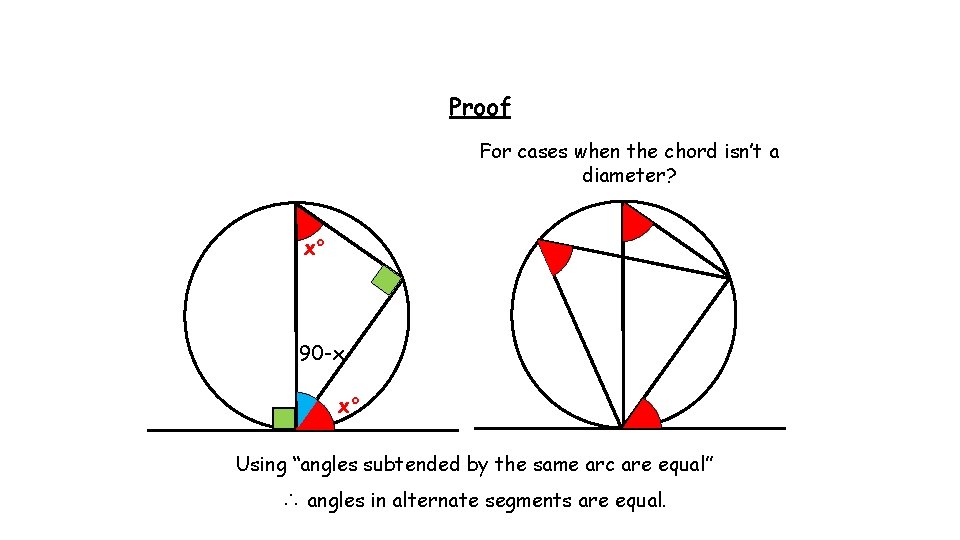
Proof For cases when the chord isn’t a diameter? x° 90 -x x° Using “angles subtended by the same arc are equal” ∴ angles in alternate segments are equal.

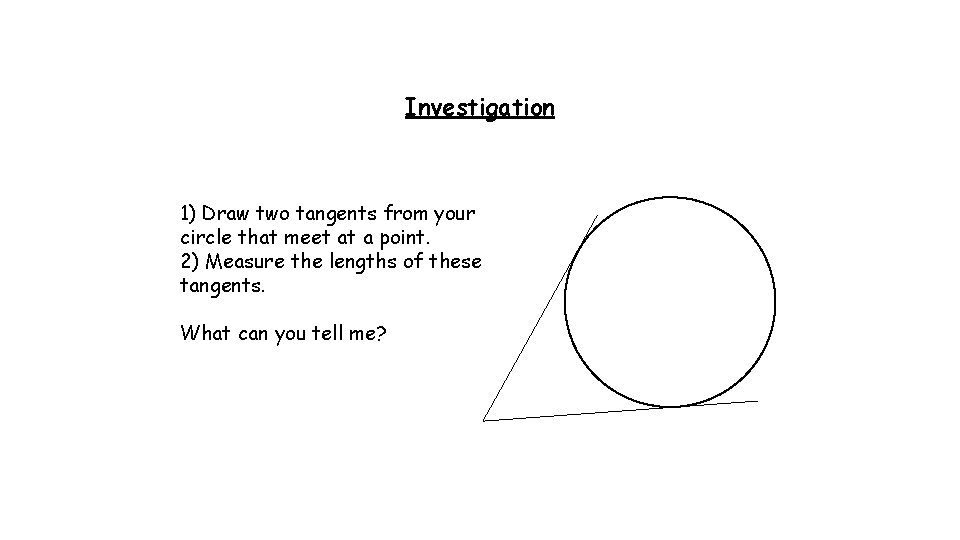
Investigation 1) Draw two tangents from your circle that meet at a point. 2) Measure the lengths of these tangents. What can you tell me?

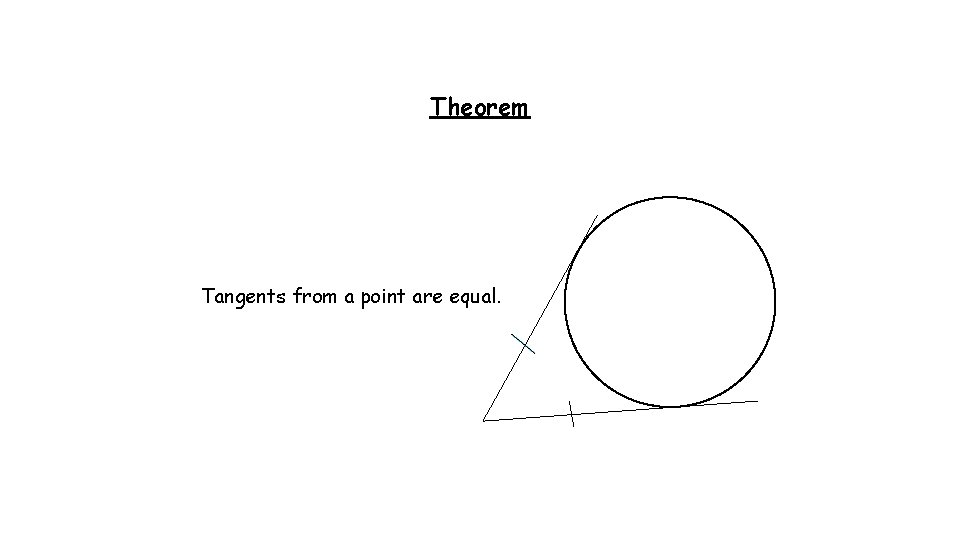
Theorem Tangents from a point are equal.

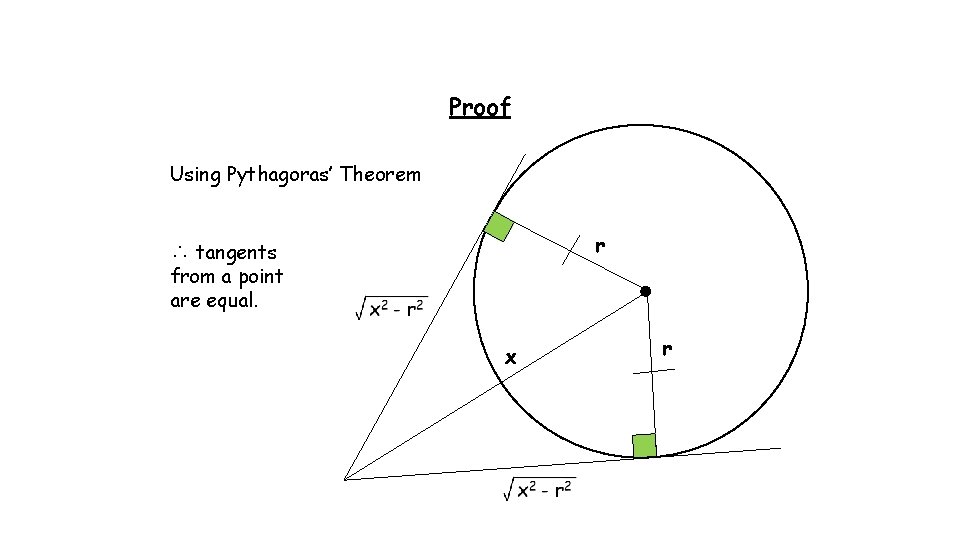
Proof Using Pythagoras’ Theorem r ∴ tangents from a point are equal. x r

Show me a problem that can be solved using: • Angle at the centre rule. • Angles subtended from an arc. • Angles subtended from the diameter. • Opposite angles in a cyclic quadrilateral.

Circle Theorems

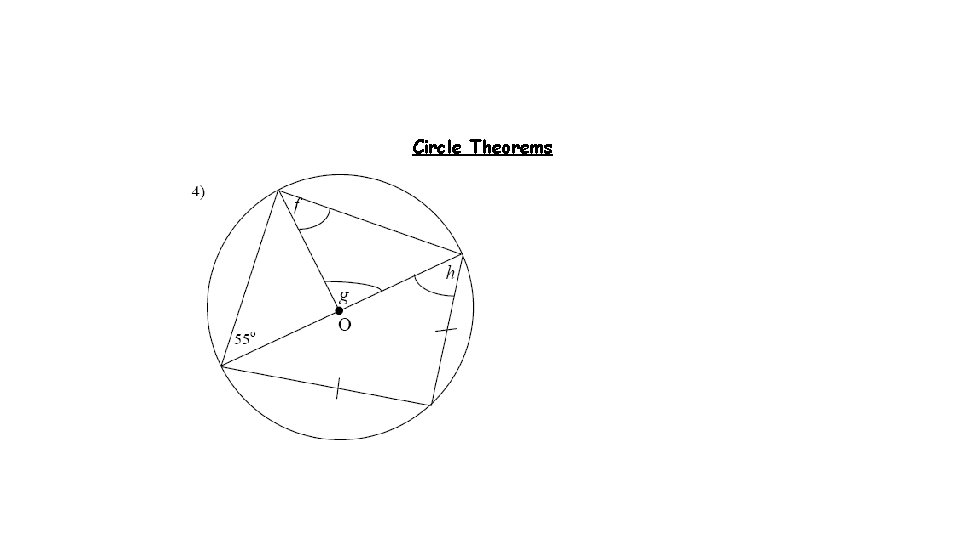
Answers 1) 2) 3) 4) 5) 6) 7) 8) 9) 10) 11) 12) 67º because angles subtended by the same arc are equal. 56º because the angle at the centre is twice that at the circumference. 69º because the angle in a semi-circle is 90º. 37º because the radii make an isosceles triangle. 109º because the radii make an isosceles triangle. 44º because angles subtended by the same arc are equal. 111º because opposite angles in a cyclic quadrilateral sum to 180º. 90º because the tangent and the radius are perpendicular. 29º because angles in alternate segments are equal. 67º because opposite angles in a cyclic quadrilateral sum to 180º. 90º because the tangent and the radius are perpendicular. 27º because angles in alternate segments are equal.