Starter Find the distance between the points 6

Starter Find the distance between the points: (6, -2) and (1, 2) distance = 6. 4 units (3, -2) and (1, -6) distance = 4. 47 units

STARTER Francisco’s house is located 3 km due east of the town library. Margerita’s house is located 4 km south and 1 km west of the same town library. Calculate how far their houses are located from the town library in a direct route. 3 km and √ 17 km Calculate how far their houses are apart from each other. √ 32 km

Investigation Consider the two numbers 6 and 10. The number exactly halfway between them, their MIDPOINT, is 8. The midpoint can easily be worked out by counting inwards from 6 and 10, but you can also find the midpoint by averaging the two numbers. This averaging is a really useful process when the numbers are not as easy to work with as 6 and 10

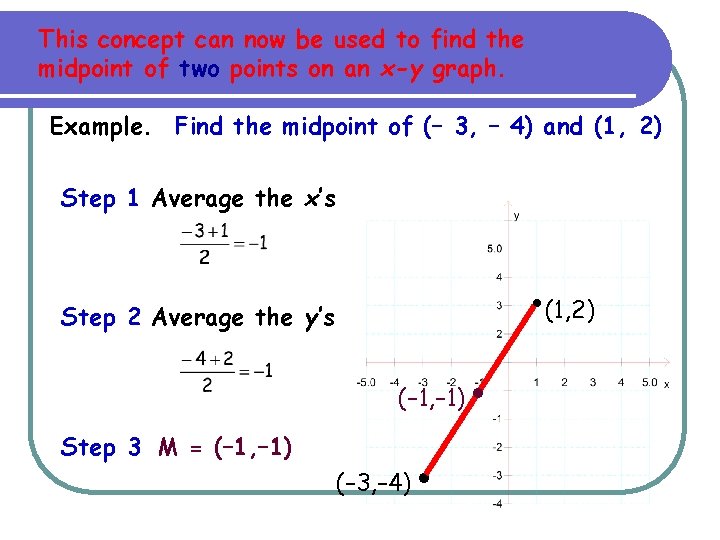
This concept can now be used to find the midpoint of two points on an x-y graph. Example. Find the midpoint of (– 3, – 4) and (1, 2) Step 1 Average the x’s • (1, 2) Step 2 Average the y’s (– 1, – 1) Step 3 M = (– 1, – 1) (– 3, – 4) • •

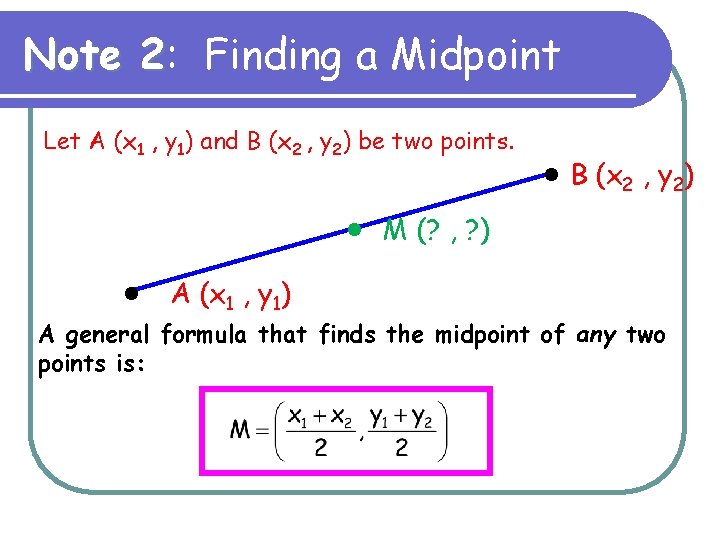
Note 2: 2 Finding a Midpoint Let A (x 1 , y 1) and B (x 2 , y 2) be two points. A (x 1 , y 1) B (x 2 , y 2) M (? , ? ) A general formula that finds the midpoint of any two points is:

Example: Find the midpoint of the line segment joining E = (10, -3) and F = (6, 0) (6 , 0) (x 1 , y 1) (10, -3) (x M = (8, -1. 5) 2 , y 2)

Page 258 Exercise 8 B