Starter Circle Geometry Example 1 A circle has







- Slides: 14

Starter: •


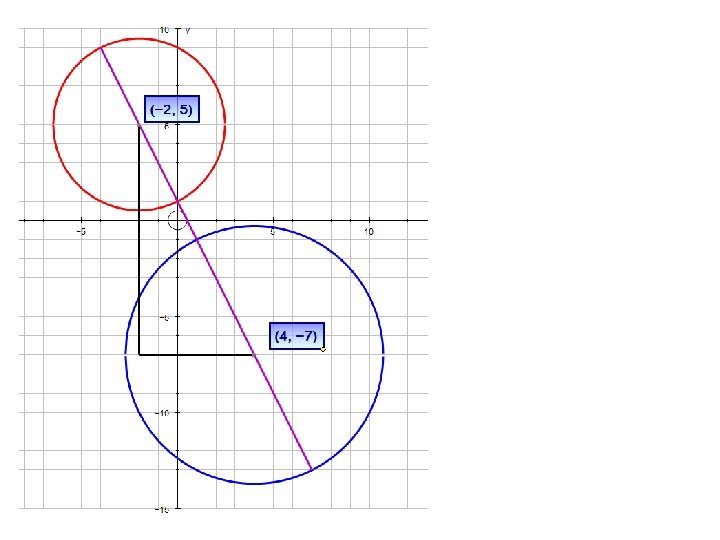
Circle Geometry: Example 1 A circle has equation x 2 + y 2 – 8 x − 28 y + 122 = 0. a) Find the co-ordinates of the centre of the circle and the radius. b) Find the co-ordinates of the points where the circle intersects the straight line y = 3 x + 2.

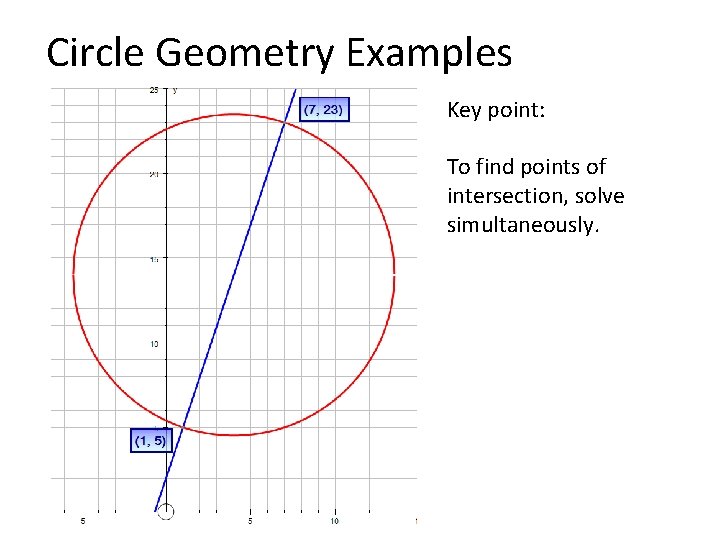
Circle Geometry Examples Key point: To find points of intersection, solve simultaneously.

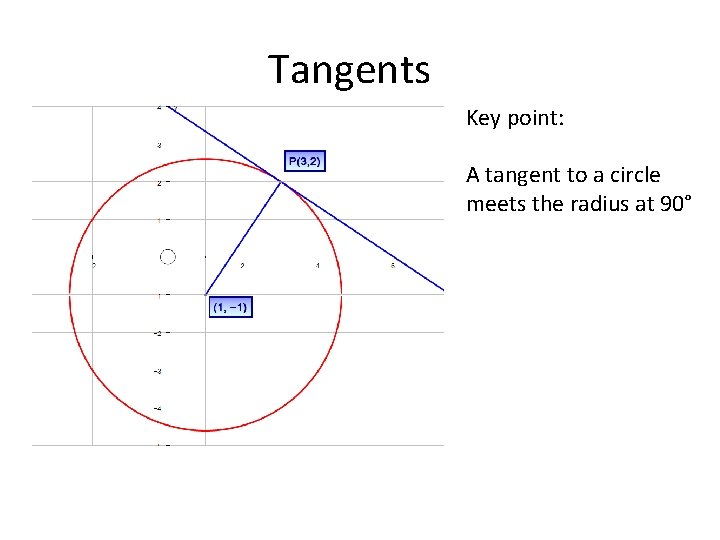
Tangents

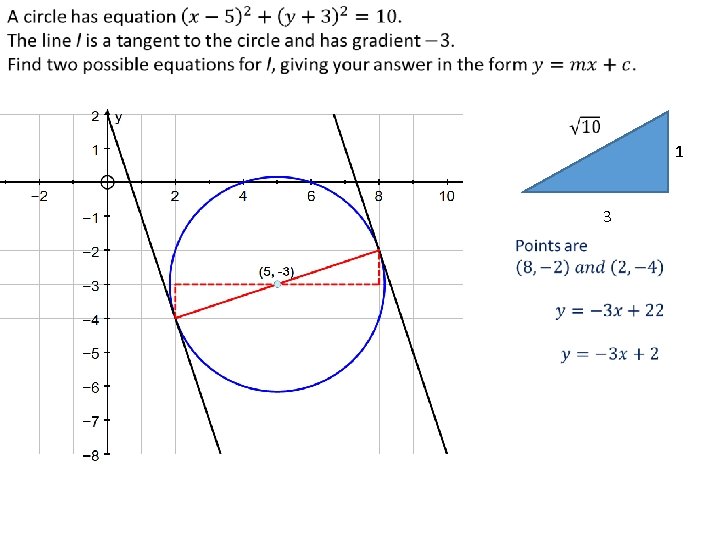
Tangents Key point: A tangent to a circle meets the radius at 90°

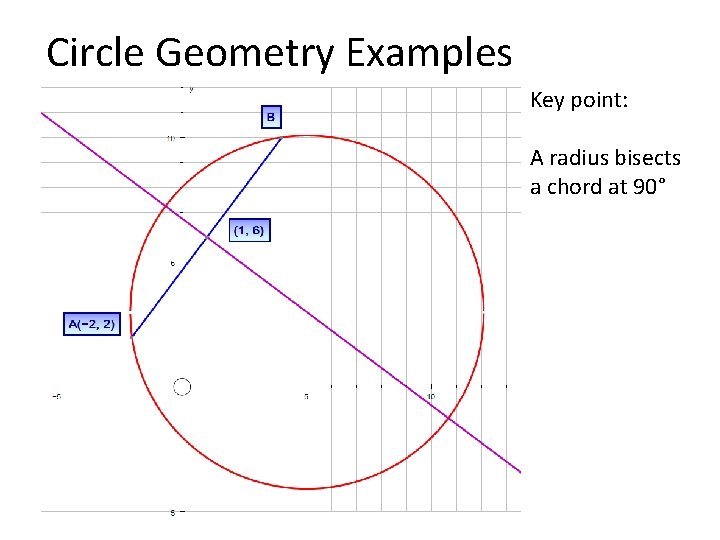
Circle Geometry: Example 2 Points A and B lie on a circle, and the line AB is a chord of the circle. Point A has co-ordinates (− 2, 2) and the mid-point of line AB has co-ordinates (1, 6). a) Line L 1 passes through the mid-point of AB and the centre of the circle. Find an equation for L 1. b) Show that the point with co-ordinates (5, 3) lies on L 1. c) Given that the centre of the circle is at the point with co-ordinates (5, 3), find an equation for the circle.

Circle Geometry Examples Key point: A radius bisects a chord at 90°

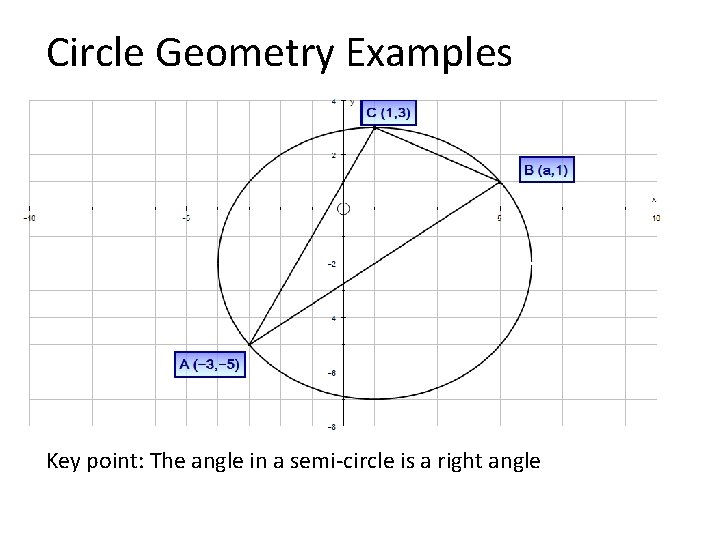
Circle Geometry: Example 3 Points A, B and C lie on a circle. A has co-ordinates (− 3, − 5), B has co-ordinates (a, 1) and C has co-ordinates (1, 3). AB is a diameter of the circle. a) Show that a = 5. b) Find an equation for the circle.

Circle Geometry Examples Key point: The angle in a semi-circle is a right angle

Circle Geometry: Example 4 A circle C has equation x 2 + y 2 + 8 x − 18 y + 61 = 0. a) The circle crosses the y – axis at the points A and B. Find the co-ordinates of A and B giving your answers as simplified surds. b) Find the co-ordinates of the centre of the circle. c) Find the radius of the circle. d) A line through the point Q(2, 1) is a tangent to the circle C at the point T. Find the length of QT. Challenge for legends: Find the possible coordinates of T. https: //www. youtube. com/watch? v=U 1 g. TUA 9 A 6 k&list=PLV_b. JOUEvt. Dm. Taov. WAm. Oay. Ub. T 00 o. OFr. T_&index=105

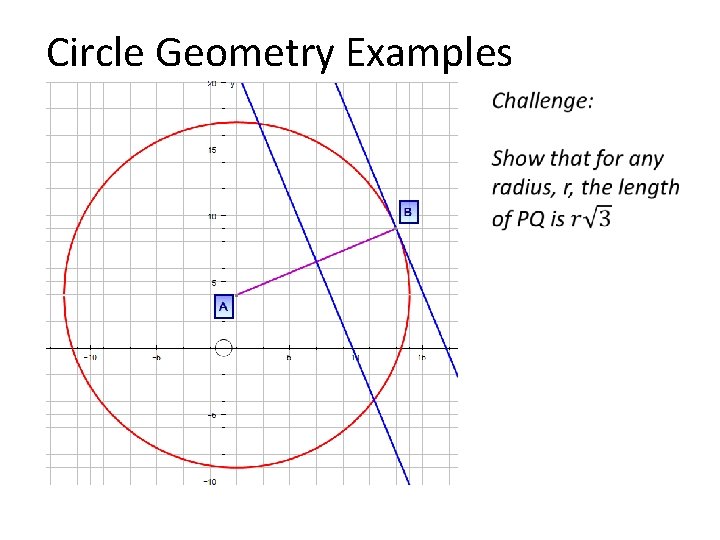
Circle Geometry: Example 5 https: //www. youtube. com/wa tch? v=22 Stfvp. JR 8 g&list=PLV_b JOUEvt. Dm. Taov. WAm. Oay. Ub. T 0 0 o. OFr. T_&index=106

Circle Geometry Examples

1 3