Stanford Streaming Supercomputer Eric Darve Mechanical Engineering Department

Stanford Streaming Supercomputer Eric Darve Mechanical Engineering Department Stanford University

Overview of Streaming Project • Main PIs: – Pat Hanrahan, hanrahan@graphics. stanford. edu – Bill Dally, billd@csl. stanford. edu • Objectives: – Cost/Performance: 100: 1 compared to clusters. – Programmable: applicable to large class of scientific applications. – Porting and developing new code made easier: stream language, support of legacy codes. 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 2

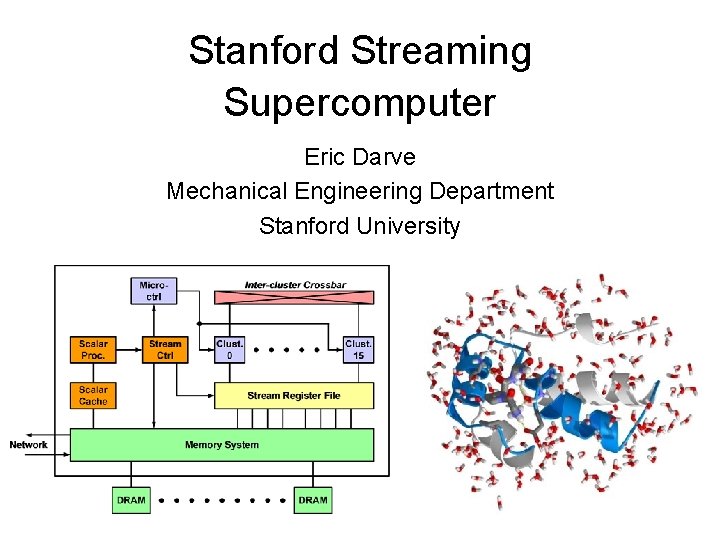
Performance/Cost Item Cost Per Node Processor chip 200 Router chip 200 50 20 3000 188 50000 49 1 50 Memory chip Board/Backplane Cabinet Power Per-Node Cost 976 Cost estimate – about $1 K/node Preliminary numbers, parts cost only, no I/O included. Expect 2 x to 4 x to account for margin and I/O 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 3

News Center News Releases | Publications | Resources | Multimedia Gallery News Release Archive | Awards FOR IMMEDIATE RELEASE October 21, 2002 Sandia National Laboratories and Cray Inc. finalize $90 million contract for new supercomputer Collaboration on Red Storm System under Department of Energy’s Advanced Simulation and Computing Program (ASCI) ALBUQUERQUE, N. M. and SEATTLE, Wash. — The Department of Energy’s Sandia National Laboratories and Cray Inc. (Nasdaq NM: CRAY) today announced that they have finalized a multiyear contract, valued at approximately $90 million, under which Cray will collaborate with Sandia to develop and deliver a new massively parallel processing (MPP) supercomputer called Red Storm. In June 2002, Sandia reported that Cray had been selected for the award, subject to 12/10/2002 successful contract. Eric negotiations. Darve - Stanford Streaming Supercomputer 4

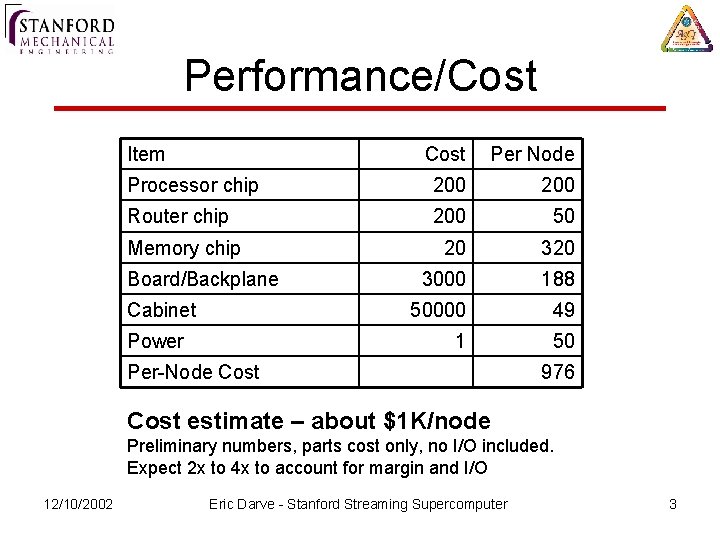
Performance/Cost Comparisons • Earth Simulator (today) – Peak 40 TFLOPS, ~$450 M – 0. 09 MFLOPS/$ – Sustained 0. 03 MFLOPS/$ • Red Storm (2004) – Peak 40 TFLOPS, ~$90 M – 0. 44 MFLOPS/$ • SSS (proposed 2006) – Peak 40 TFLOPS, < $1 M – 128 MFLOPS/$ – Sustained 30 MFLOPS/$ (single node) • Numbers are sketchy today, but even if we are off by 2 x, improvement over status quo is large 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 5

ES Red. Storm ASCI machines SSS Desktop SSS 12/10/2002 GFLOPS Eric Darve - Stanford Streaming Supercomputer 6

How did we achieve that? 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 7

VLSI Makes Computation Plentiful VLSI: very large-scale integration. This is the current level of computer microchip miniaturization (refers to microchips containing in the hundreds of thousands of transistors. ) • Abundant, inexpensive arithmetic – Can put 100 s of 64 -bit ALUs on a chip – 20 p. J per FP operation • (Relatively) high off-chip bandwidth – 1 Tb/s demonstrated, 2 n. J per word off chip • Memory is inexpensive $100/Gbyte n. Vidia Ge. Force 4 ~120 Gflops/sec ~1. 2 Tops/sec Velio VC 3003 1 Tb/s I/O BW 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 8

But VLSI imposes some constraints Current Architecture: few ALUs / chip = expensive and limited performance. 64 -bit ALU (to scale) Chip Architecture of Pentium 4 Objective for SSS architecture: • Keep hundreds of ALUs/chip busy. Difficulty: • Locality of data: we need to match 20 Tb/s ALU bandwidth to ~100 Gb/s chip bandwidth. • Latency tolerance: to cover 500 cycle remote memory access time. Arithmetic is cheap, global bandwidth is expensive Eric Darve - Stanford Streaming Supercomputer Local << global on-chip << off-chip << global system 12/10/2002 9

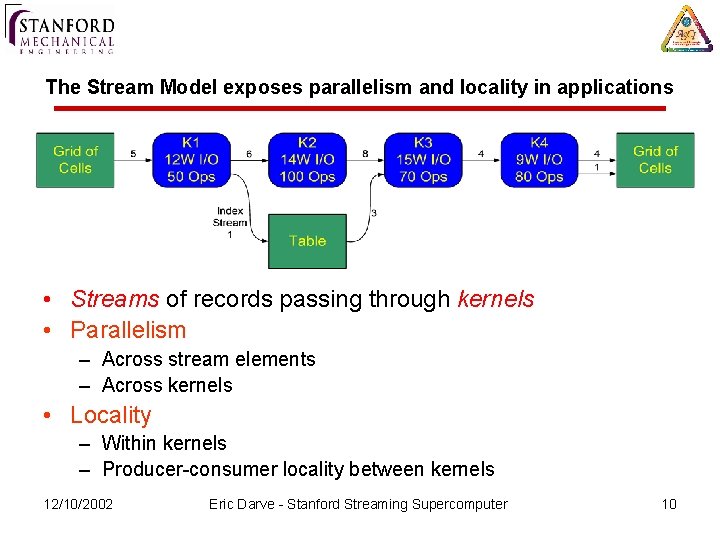
The Stream Model exposes parallelism and locality in applications • Streams of records passing through kernels • Parallelism – Across stream elements – Across kernels • Locality – Within kernels – Producer-consumer locality between kernels 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 10

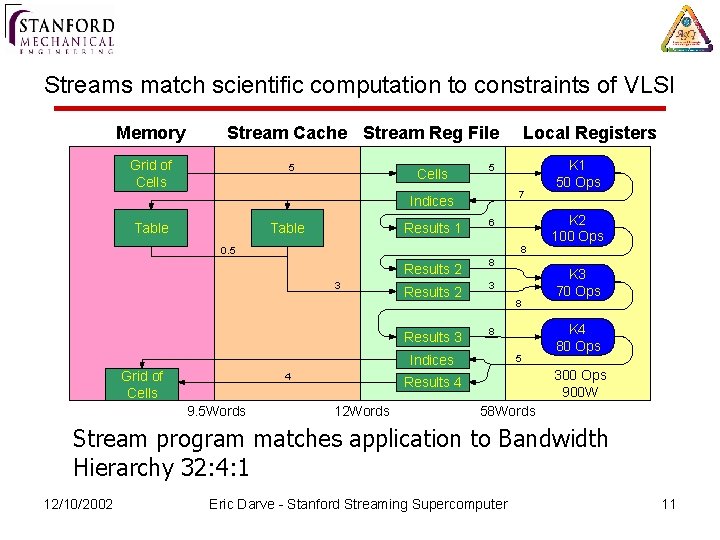
Streams match scientific computation to constraints of VLSI Memory Stream Cache Stream Reg File Grid of Cells 5 7 Indices Table Results 1 6 Results 2 8 Results 2 3 Results 3 8 8 0. 5 3 8 Indices Grid of Cells 4 9. 5 Words Local Registers 5 K 2 100 Ops K 3 70 Ops K 4 80 Ops 300 Ops 900 W Results 4 12 Words K 1 50 Ops 58 Words Stream program matches application to Bandwidth Hierarchy 32: 4: 1 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 11

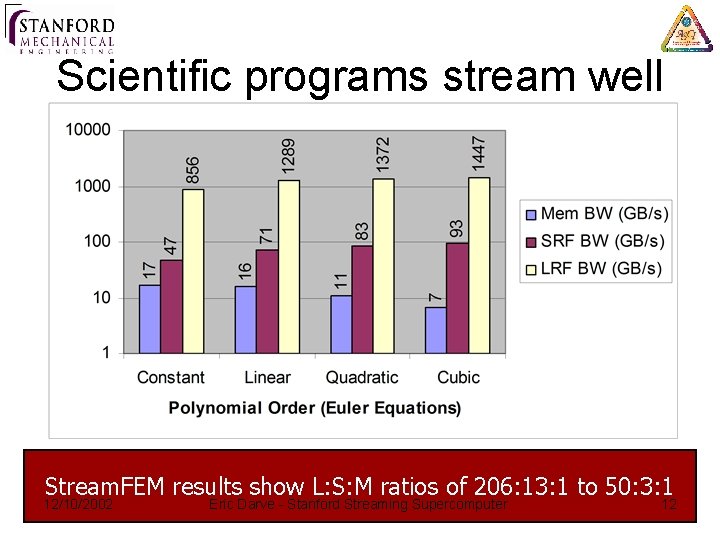
Scientific programs stream well Stream. FEM results show L: S: M ratios of 206: 13: 1 to 50: 3: 1 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 12

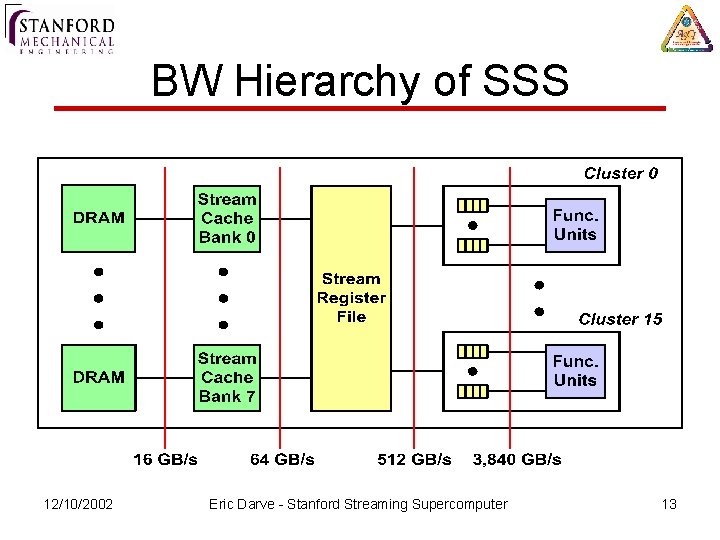
BW Hierarchy of SSS 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 13

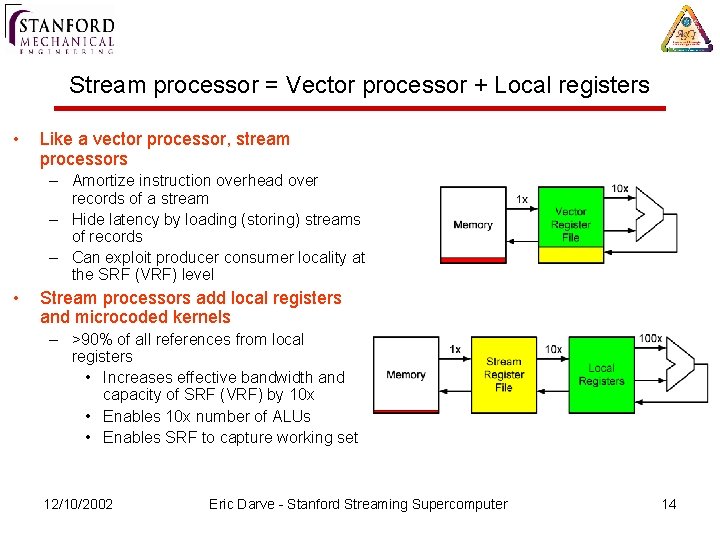
Stream processor = Vector processor + Local registers • Like a vector processor, stream processors – Amortize instruction overhead over records of a stream – Hide latency by loading (storing) streams of records – Can exploit producer consumer locality at the SRF (VRF) level • Stream processors add local registers and microcoded kernels – >90% of all references from local registers • Increases effective bandwidth and capacity of SRF (VRF) by 10 x • Enables 10 x number of ALUs • Enables SRF to capture working set 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 14

Brook: streaming language • C with streaming – Make data parallelism explicit – Declare communication pattern • Streams – View of records in memory – Operated on in parallel – Accessing stream values not is permitted outside of kernels Kernel 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 15

Brook Kernels • Kernels – Functions which operate only on streams • Stream arguments are read-only or write-only • Reduction variables (associative operations only) – Restricted communication between records • No state or “static” variables • No global memory access Kernel 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 16

Brook Example: Molecular Dynamics struct Vector { float x, y, z ; } ; typedef stream struct Vectors ; kernel void Update. Position ( Vectors s. Pos, Vectors s. Vel, const float timestep, out Vectors s. New. Pos ) { s. New. Pos. x = s. Pos. x + timestep * s. Vel. x; s. New. Pos. y = s. Pos. y + timestep * s. Vel. y; s. New. Pos. z = s. Pos. z + timestep * s. Vel. z; } 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 17

struct Vector { float x, y, z ; } ; typedef stream struct Vectors ; void main () { struct Vector Pos[MAX] = {…} ; struct Vector Vel[MAX] = {…} ; Vectors s. Pos, s. Vel, s. New. Pos ; stream. Load (s. Pos, MAX) ; stream. Load (s. Vel, MAX) ; Update. Position (s. Pos, s. Vel, 0. 2 f, s. New. Pos) ; stream. Store (s. New. Pos, Pos) ; } 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 18

Stream. MD: motivation • Application: study the folding of human proteins. • Molecular Dynamics: computer simulation of the dynamics of macro molecules. • Why this application? • DNA molecule – Expect high arithmetic intensity. – Requires variable length neighborlists. – Molecular Dynamics can be used in engine simulation to model spray, e. g. droplet formation and breakup, drag, deformation of droplet. Test case chosen for initial evaluation: box of water molecules. Human immunodeficiency virus (HIV) 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 19

Numerical Algorithm • Interaction between atoms is modeled by the potential energy associated to each configuration. Includes: – Chemical bond potentials. – Electrostatic interactions. – Van der Waals interactions. • Newton’s second law of motion used to compute the trajectory of all atoms: • Velocity Verlet time integrator (leap-frog): 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 20

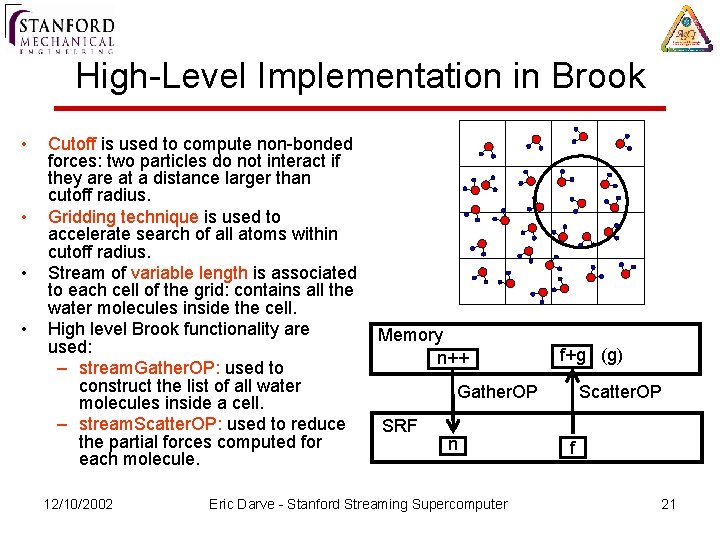
High-Level Implementation in Brook • • Cutoff is used to compute non-bonded forces: two particles do not interact if they are at a distance larger than cutoff radius. Gridding technique is used to accelerate search of all atoms within cutoff radius. Stream of variable length is associated to each cell of the grid: contains all the water molecules inside the cell. High level Brook functionality are used: – stream. Gather. OP: used to construct the list of all water molecules inside a cell. – stream. Scatter. OP: used to reduce the partial forces computed for each molecule. 12/10/2002 Memory n++ f+g (g) Gather. OP SRF n Eric Darve - Stanford Streaming Supercomputer Scatter. OP f 21

Stream. MD Results 100 120 FSUB FLT FABS FSUB SELECT FLT SELECT FSUB SELECT FLT FSUB FSUB SPREAD FSUB FMUL FSUB FMUL FADD FMUL FSUB SPREAD FMUL FSUB FMUL FADD FMUL FINVSQRT_LOOKUP FSUB PASS FADD FSUB FMUL FADD FSQRT FMUL SPREAD FMUL FSUB FMUL FADD FSUB FADD FMUL SPREAD FMUL FSUB FMUL FSQRT FSUB FADD FMUL FSUB FMUL FADD FMUL FSUB FDIV FMUL FADD FMUL FSUB FMUL FMUL FSQRT FMUL FADD FSUB FMUL FINVSQRT_LOOKUP FMUL FADD FMUL FMUL FMUL PASS FINVSQRT_LOOKUP FSUB FMUL PASS FINVSQRT_LOOKUP FSUB PASS FMUL FINVSQRT_LOOKUP FADD FMUL PASS FMUL FSUB FMUL FMUL FINVSQRT_LOOKUP FSUB FMUL FINVSQRT_LOOKUP FMUL FSUB PASS FSUB FMUL FSUB FDIV FMUL FSUB FMUL PASS FMUL FSUB SPREAD FSUB FMUL FSUB 220 FSQRT FSUB FMUL FSUB FSQRT FMUL FSUB FMUL FADD FMUL FMUL FMUL FADD PASS FMUL PASS FSUB FMUL FDIV FMUL FADD FMUL FSUB FMUL FADD FMUL FDIV FSUB FMUL FMUL FADD FSUB PASS FMUL FSUB FMUL SPREAD FMUL FSUB FMUL PASS FMUL FSUB FMUL PASS FMUL FADD FMUL FSUB FMUL FADD FSQRT FLE FMUL FDIV FMUL FMUL FADD FMUL FMUL PASS FMUL FMUL FADD FMUL FSQRT FMUL FADD FMUL 280 FMUL FADD PASS FMUL FADD FMUL FLE FADD FMUL FADD FADD FSUB FLE FADD FADD FADD 340 FADD FADD FADD FSUB FADD FADD FADD FSUB FADD FADD FSUB FADD FADD FMUL FMUL FMUL FMUL FMUL FMUL FMUL FMUL FMUL FMUL FMUL FMUL FMUL FMUL FADD FDIV FMUL FMUL FMUL FSUB PASS FMUL FADD FMUL FMUL PASS FMUL SELECT FADD FMUL FADD FMUL PASS FADD FADD FADD FSUB FMUL FADD FSUB PASS FMUL SPREAD SELECT FMUL PASS FADD PASS FSUB FMUL SELECT SELECT SPREAD SPWRITE SELECT Imagine 260 DATA_OUT NSELECT FADD DATA_OUT FMUL FADD FMUL FMUL FMUL FADD FMUL FADD FMUL FADD PASS NSELECT PASS FMUL PASS FMUL FADD PASS FADD FADD PASS NSELECT FMUL FADD SPREAD NSELECT NSELECT FSUB FADD 32 T DEC_CHK_UCR DEC_UCR SPREAD FSUB FADD PASS FMUL PASS FMUL FADD PASS NSELECT PASS FMUL FADD FSUB PASS FMUL FSUB SPWRITE SELECT SPWRITE LOOP SPWRITE PASS FLE FADD PASS SPREAD SELECT FMUL FADD PASS FMUL FMUL PASS FMUL NSELECT 12/10/2002 FMUL 32 IADD FMUL NSELECT FMUL FSUB FADD FMUL FMUL FADD PASS FMUL FMUL FMUL PASS FMUL 220 FSQRT FMUL FADD PASS FADD PASS FSUB FINVSQRT_LOOKUP FSUB FMUL FADD PASS FMUL FINVSQRT_LOOKUP FMUL FDIV FINVSQRT_LOOKUP FADD FMUL 170 FMUL FSUB FMUL FADD FSQRT FSUB FADD FMUL FSUB PASS FMUL FADD FMUL FSUB FADD PASS FMUL FADD FMUL FDIV FMUL FSUB FADD FMUL FSUB • Preliminary schedule obtained using the Imagine architecture: – High arithmetic intensity: all ALUs are kept busy. Gflops expected to be very high. – SRF bandwidth is sufficient. About 1 word for 30 instructions. • Results helped guide architectural decisions for SSS. SPREAD PASS FMUL FADD FMUL FSUB 160 FSUB FMUL FADD FSUB FDIV FSUB FMUL PASS SPREAD FSUB FADD NSELECT SPREAD FSUB FDIV NSELECT SPREAD FSUB SELECT SPREAD PASS SPREAD SELECT SPWRITE SELECT SPWRITE SELECT DEC_CHK_UCR SPWRITE DEC_UCR LOOP PASS DATA_OUT NSELECT SSS Eric Darve - Stanford Streaming Supercomputer 22

Observations • Arithmetic intensity is sufficient. Bandwidth is not going to be the limiting factor in these applications. Computation can be naturally organized in a streaming fashion. • The interaction between the application developers and the language development group has helped insured that Brook can be used to code real scientific applications. • Architecture has been refined in the process of evaluating these applications. • Implementation is much easier than MPI. Brook hides all the parallelization complexity from the user. The code is very clean and easy to understand. The streaming versions of these applications are in the range of 1000 -5000 lines of code. 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 23

A GPU is a stream processor • The GPU on a Graphics Card is streaming processor. • n VIDIA recently announced that their latest graphics card, the NV 30, will be programmable and capable of delivering 51 Gflops peak performance (1. 6 Gflops for Pentium 4). Can we use this computing power for scientific application? 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 24

Cg: Assembly or High-level? Assembly … DP 3 R 0, c[11]. xyzx; RSQ R 0, R 0. x; MUL R 0, R 0. x, c[11]. xyzx; MOV R 1, c[3]; MUL R 1, R 1. x, c[0]. xyzx; DP 3 R 2, R 1. xyzx; RSQ R 2, R 2. x; MUL R 1, R 2. x, R 1. xyzx; ADD R 2, R 0. xyzx, R 1. xyzx; DP 3 R 3, R 2. xyzx; RSQ R 3, R 3. x; MUL R 2, R 3. x, R 2. xyzx; DP 3 R 2, R 1. xyzx, R 2. xyzx; MAX R 2, c[3]. z, R 2. x; MOV R 2. z, c[3]. y; MOV R 2. w, c[3]. y; LIT R 2, R 2; . . . 12/10/2002 or Phong Shader Cg COLOR c. Plastic = Ca + Cd * dot(Nf, L) + Cs * pow(max(0, dot(Nf, H)), phong. Exp); Eric Darve - Stanford Streaming Supercomputer 25

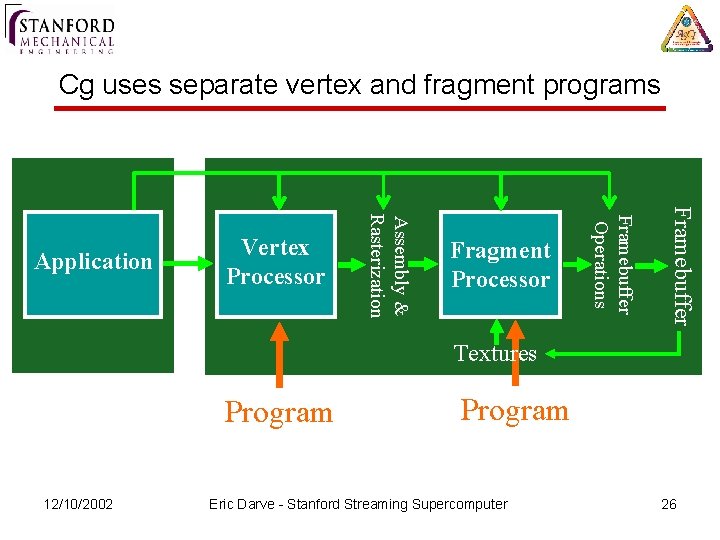
Cg uses separate vertex and fragment programs Framebuffer Fragment Processor Framebuffer Operations Assembly & Rasterization Application Vertex Processor Textures Program 12/10/2002 Program Eric Darve - Stanford Streaming Supercomputer 26

Characteristics of NV 30 & Cg • Characteristics of GPU: – optimized for 4 -vector arithmetic – Cg has vector data types and operations e. g. float 2, float 3, float 4 – Cg also has matrix data types e. g. float 3 x 3, float 3 x 4, float 4 x 4 • Some Math: – Sin/cos/etc. – Normalize • Dot product: dot(v 1, v 2); • Matrix multiply: – matrix-vector: mul(M, v); – vector-matrix: mul(v, M); – matrix-matrix: mul(M, N); 12/10/2002 // returns a vector // returns a matrix Eric Darve - Stanford Streaming Supercomputer 27

Example: MD Innermost loop in C: computation of LJ and Coulomb interactions. for (k=nj 0; k<nj 1; k++) { //loop over indices in neighborlist jnr = jjnr[k]; //get index of next j atom (array LOAD) j 3 = 3*jnr; //calc j atom index in coord & force arrays jx = pos[j 3]; //load x, y, z coordinates for j atom jy = pos[j 3+1]; jz = pos[j 3+2]; qq = iq*charge[jnr]; //load j charge and calc. product dx = ix – jx; //calc vector distance i-j dy = iy – jy; dz = iz – jz; rsq = dx*dx+dy*dy+dz*dz; //calc square distance i-j rinv = 1. 0/sqrt(rsq); //1/r rinvsq = rinv*rinv; //1/(r*r) vcoul = qq*rinv; //potential from this interaction fscal = vcoul*rinvsq; //scalarforce/|dr| vctot += vcoul; //add to temporary potential variable fix += dx*fscal; //add to i atom temporary force variable fiy += dy*fscal; //F=dr*scalarforce/|dr| fiz += dz*fscal; force[j 3] -= dx*fscal; //subtract from j atom forces force[j 3+1]-= dy*fscal; force[j 3+2]-= dz*fscal; }

Inner loop in Cg /* Find the index and coordinates of j atom */ jnr = f 4 tex 1 D (jjnr, k); /* Get the atom position */ j 1 = f 3 tex 1 D(pos, jnr. x); j 2 = f 3 tex 1 D(pos, jnr. y); j 3 = f 3 tex 1 D(pos, jnr. z); j 4 = f 3 tex 1 D(pos, jnr. w); We are fetching coordinates of atom: data is stored as texture We compute four interactions at a time so that we can take advantage of high performance of vector arithmetic. 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 29

/* Get the vectorial distance, and r^2 */ d 1 = i - j 1; d 2 = i - j 2; d 3 = i - j 3; d 4 = i - j 4; rsq. x = dot(d 1, d 1); rsq. y = dot(d 2, d 2); rsq. z = dot(d 3, d 3); rsq. w = dot(d 4, d 4); /* Calculate 1/r */ rinv. x = rsqrt(rsq. x); rinv. y = rsqrt(rsq. y); rinv. z = rsqrt(rsq. z); rinv. w = rsqrt(rsq. w); Computing the square of distance We use built-in dot product for float 3 arithmetic Built-in function: rsqrt

/* Calculate Interactions */ rinvsq = rinv * rinv; rinvsix = rinvsq * rinvsq; vnb 6 vnb 12 vnbtot qq vcoul fs vctot Highly efficient float 4 arithmetic = rinvsix * temp_nbfp; = vnb 12 - vnb 6; = iq. A * temp_charge; = qq*rinv; = (12 f * vnb 12 - 6 f * vnb 6 + vcoul) * rinvsq; = vcoul; This is the force computation /* Calculate vectorial force and update local i atom force */ fi 1 = d 1 * fs. x; fi 2 = d 2 * fs. y; fi 3 = d 3 * fs. z; fi 4 = d 4 * fs. w;

Computing total force due to 4 interactions ret_prev. fi_with_vtot. xyz+= fi 1 + fi 2 + fi 3 + fi 4; ret_prev. fi_with_vtot. w += dot(vnbtot, float 4(1, 1, 1, 1)) + dot(vctot, float 4(1, 1, 1, 1)); Computing total potential energy for this particle Return type is: struct inner_ret { float 4 fi_with_vtot; }; Contains x, y and z coordinates of force and total energy.

Conclusion • 3 representative applications show high bandwidth ratios: stream. MD, stream. Flo, Stream. FEM. • Feasibility of streaming established for scientific applications: high arithmetic intensity, bandwidth hierarchy is sufficient. • Available today: NVidia NV 30 graphics card. • Future work: – – – Stream. MD to GROMACS (Folding @ Home) Stream. FEM and Stream. FLO to 3 D Multinode versions of all applications Sparse solvers for implicit time-stepping Adaptive meshing Numerics 12/10/2002 Eric Darve - Stanford Streaming Supercomputer 33