Standardized Distributions Statistics 2126 Introduction Last time we

Standardized Distributions Statistics 2126

Introduction • Last time we talked about measures of spread • Specifically the variance and the standard deviation • s and s 2 • You might ask yourself “Why is this useful? ”

So, what did you get? • Say you are comparing your quiz marks with other people in the class • Let’s say you got 8 • And the class average was 7 • That is a population mean, we are considering the class to be a population so = 7

What did you get, in relation to others • By how much are you better than the class average • By 1…. • If everyone got say below you, you rock • This is where the population standard deviation or comes into play • Let’s say = 1. 5

So compare • How many standard deviations are you from the mean? • We call this a z score

x=8 =7 =1. 5

So what does that mean? • It means you are. 67 standard deviations away from the mean. • We now have a measure of how far away you are from a mean • We call this a standard score • Let’s say you get 8 on the next quiz • But now the class mean is 7. 5

Change it up a little • Now let’s say the standard deviation is. 5 • So now on this quiz the scores were packed much more tightly • Did you do relatively better on the first quiz or on the second one?

x=8 =7. 5 =. 5

So compare the two • You did better on the second quiz than you did on the first one • You are 1 standard deviation from the mean • You are simply comparing the two z scores

Properties of z • It can be negative or positive • If you are off to the left of the mean you will get a negative score • If you are off to the right, your z score will be positive • What is the shape? • What is the average z score? • What is the standard deviation?

You can answer these questions by looking at the formula

An example • IQ has a mean of 100 and a standard deviation of 15 • N(100, 15) • That just means it is normal with a mean of 100 and a sd of 15 • So what is the z score of someone with an IQ of 118

x = 118 = 100 = 15

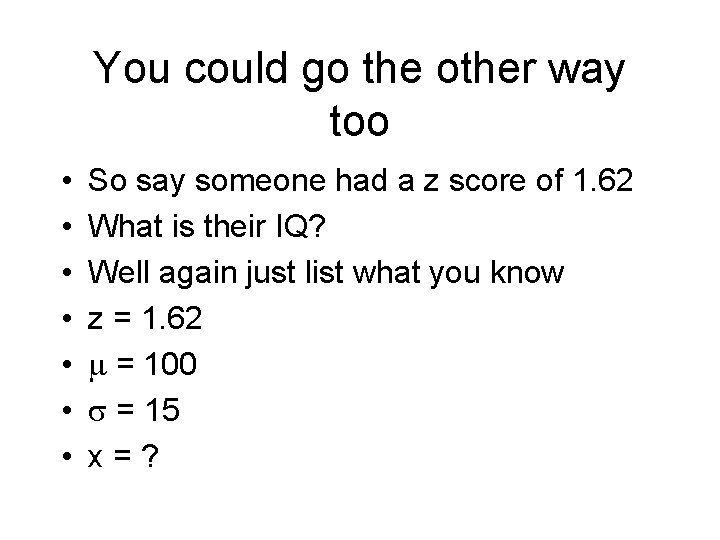
You could go the other way too • • So say someone had a z score of 1. 62 What is their IQ? Well again just list what you know z = 1. 62 = 100 = 15 x=?

Now just sub into the formula and cross multiply

Well this must all have a point • Using a z table • Or this VERY cool website: • http: //davidmlane. com/hyperstat/z_table. html • So if you know the z, you can find out what the probability of getting a z score at a certain level is.

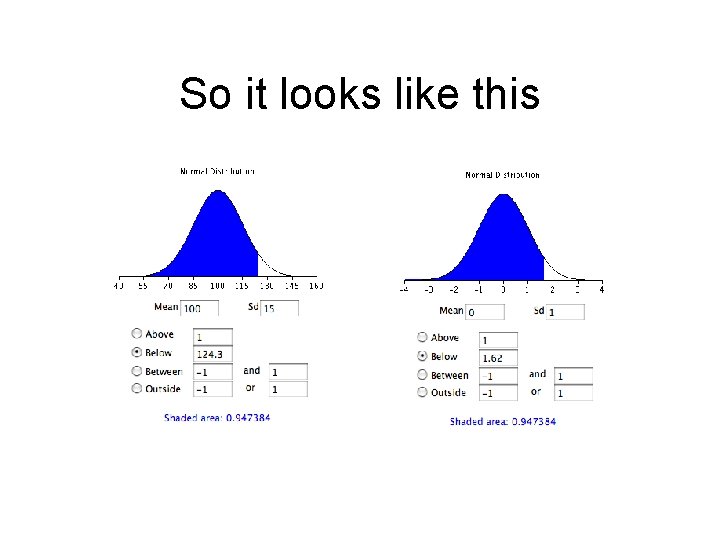
So it looks like this