Standardization the properties of objective tests Properties of

Standardization the properties of objective tests

Properties of Objective Tests l There are three standards by which you can judge an objective test l Standardization l Reliability l Validity

Properties of Objective Tests l Standardization – scoring & use of scores does not vary across situations l Reliability – scores are consistent and remain stable over time l Validity – the test measures what it intends to measure

Standardization Principles l Objective Scoring l Directions l Consistency l Accuracy and timeliness

Standardization Principles l Administration l Appropriate conditions specified l Materials l Probing / Coaching

Standardization Principles l Guidelines for interpretation and use l With whom? l For what purpose? l What do high and low scores mean?

Standardization Principles l Norm tables l Based on large l Representative samples l From a defined population

Standardization Principles l Specialized norm tables l Subgroup differences l For example: age, gender, race, primary language, etc.

Standardization Principles l Raw scores and standard scores provided where appropriate l Standard scores l Percentile ranks l Age standardized scores

Standardization Principles l Technical manual l Test development process l Guidelines for administration, scoring, and interpretation l Norm tables l Meets standards for Ed. & Psych. tests

Norm Tables l Meaningful for interpretation when: l Norm referenced interpretation meets the goal of the test l Not a criterion referenced test

Norm Tables l Meaningful for interpretation when: l Relative position in a group has interpretative meaning l Examinee is a member of the population

Norm Tables l Meaningful for interpretation when: l The norm sample is large and representative of the population l The right norm table is used

Norm Tables l All those taking the test for a given administration may work as a norm sample for an admissions or personnel selection purpose

Norm Tables l However, the correct reference group varies by the purpose l Career counseling l Placement in the appropriate courses l Selection for a remedial program

Interpreting Standard Scores l Raw score is transformed into a standard score l z = (score – mean)/SD l z score = SDs units away from mean l Includes measure of middle and spread

Interpreting Standard Scores l z = 0, average score l z <=-1, low score l z >=1, high score l z is converted to some other scaling: l Mean l SD 50 10 100 15 500 100

Interpreting Standard Scores l pp. 42, 43, 48 in book give guidelines l Easiest to use when converted to percentiles l % of population that scores at or below a given score l Can be thought of as a rank out of 100 members of the population

Interpreting Standard Scores l Common interpretation strategies: l Normal range is middle 68% of the population (T=40 -60, z=-1 to 1, etc. ) l Low and high scores fall outside this range (lower and upper 16%)

Interpreting Standard Scores l Common interpretation strategies: l Normal range is middle 50% of the population (Quartiles 2 & 3) l Low and high scores fall outside this range (Quartiles 1 and 4)

Interpreting Standard Scores l Safer to make broad classification like “Low”, “Within the normal, or expected, range”, or “High” than fine distinctions. l All scores have some measurement error in them. l Look for patterns across the battery, across multiple sources.

An Example from WCCS l Christina, a 1 st grade student at our school, took the Stanford Achievement Test last year. Here are her Word Study Skills subtest scores.

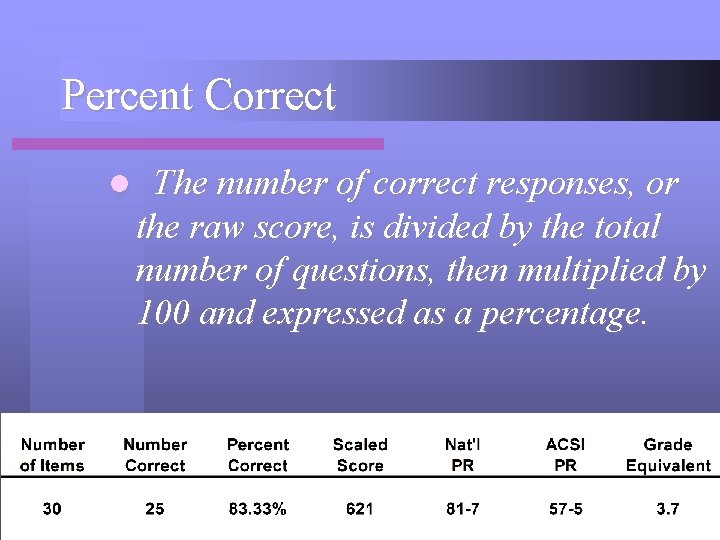
Percent Correct l The number of correct responses, or the raw score, is divided by the total number of questions, then multiplied by 100 and expressed as a percentage.

Percent Correct l Christina gave the correct answer to 83. 33% of the questions on the Word Study Skills section of the test.

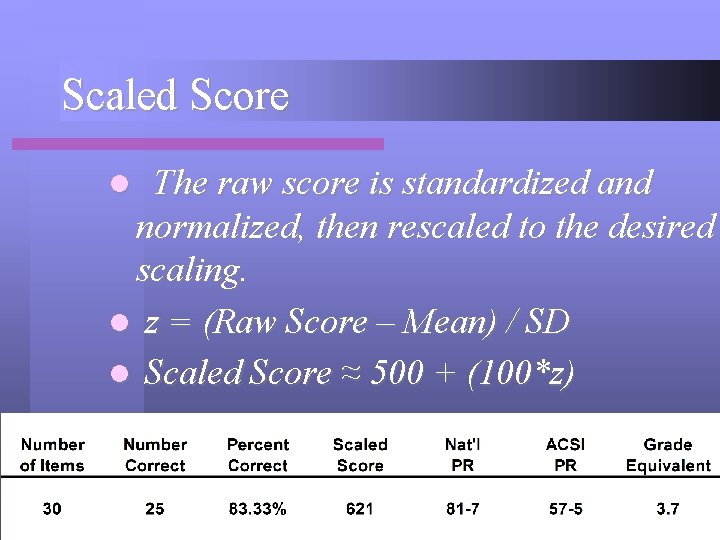
Scaled Score The raw score is standardized and normalized, then rescaled to the desired scaling. l z = (Raw Score – Mean) / SD l Scaled Score ≈ 500 + (100*z) l

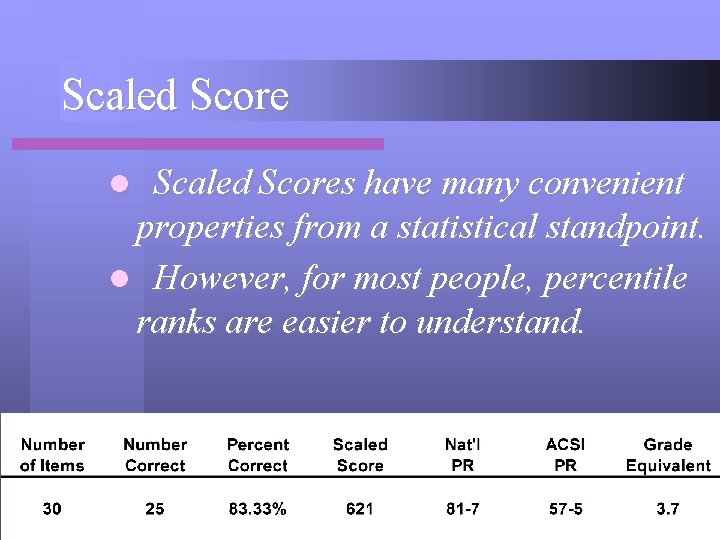
Scaled Scores have many convenient properties from a statistical standpoint. l However, for most people, percentile ranks are easier to understand. l

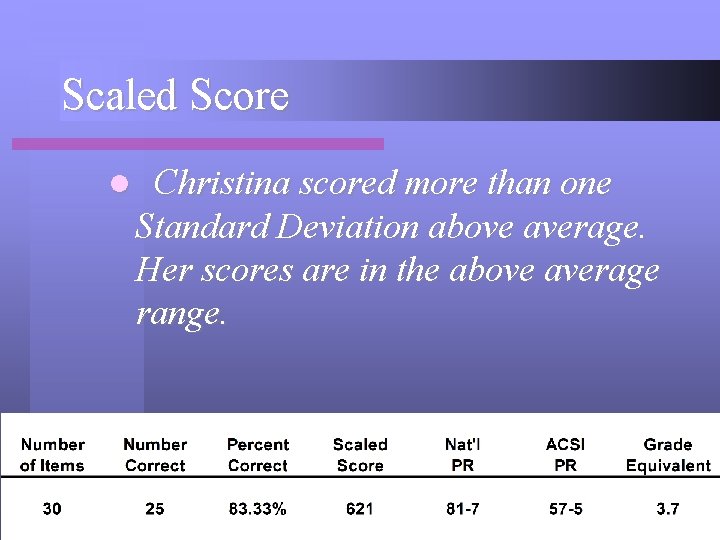
Scaled Score l Christina scored more than one Standard Deviation above average. Her scores are in the above average range.

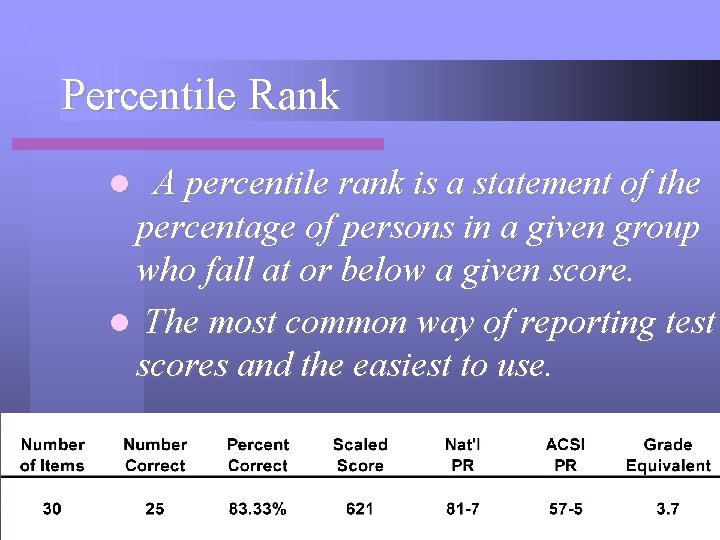
Percentile Rank A percentile rank is a statement of the percentage of persons in a given group who fall at or below a given score. l The most common way of reporting test scores and the easiest to use. l

Percentile Rank l Christina scored as well or better than 81% of all students in the nation who took this section of the test.

Percentile Rank l Christina scored as well or better than 57% of all students in ACSI schools who took this section of the test.

Percentile Rank l This pattern is typical for our students on average. – ≈ 80 th percentile nationally – ≈ 60 th percentile for ACSI students – What does this mean?

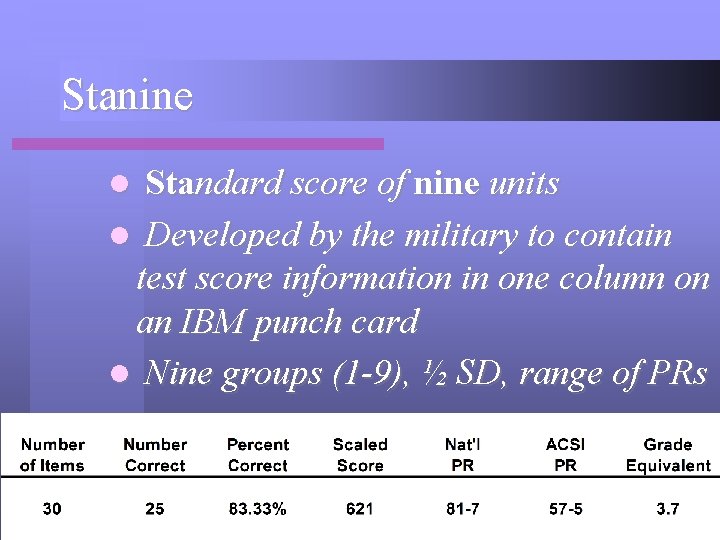
Stanine Standard score of nine units l Developed by the military to contain test score information in one column on an IBM punch card l Nine groups (1 -9), ½ SD, range of PRs l

Stanine Christina’s scores fall in the 7 th stanine, or above average compared to all students nationally. l Christina’s scores fall in the 5 th stanine, or average for ACSI students. l

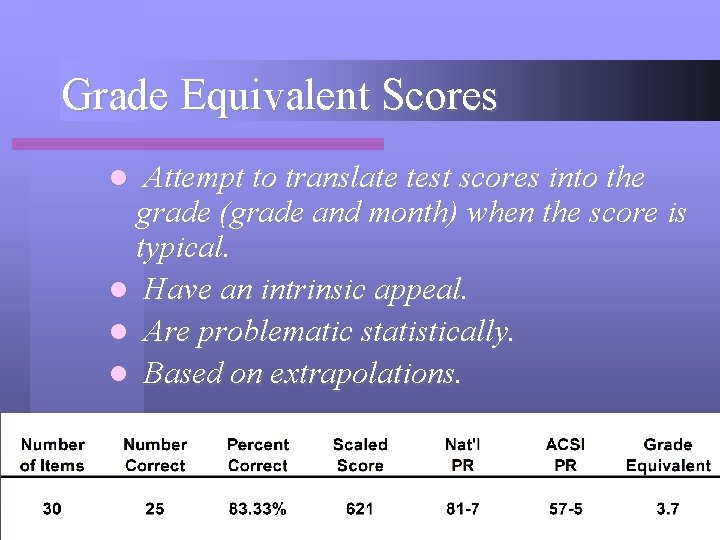
Grade Equivalent Scores Attempt to translate test scores into the grade (grade and month) when the score is typical. l Have an intrinsic appeal. l Are problematic statistically. l Based on extrapolations. l

Grade Equivalent Scores l Christina, a 1 st grade student at our school, in the area of Word Study Skills, is performing at the level of a typical 3 rd grade student in the seventh month of the school year (on the 1 st grade test).

An SAT Example l Mark, a 12 th grade student at our school, took the SAT test last year. Here are his scores.

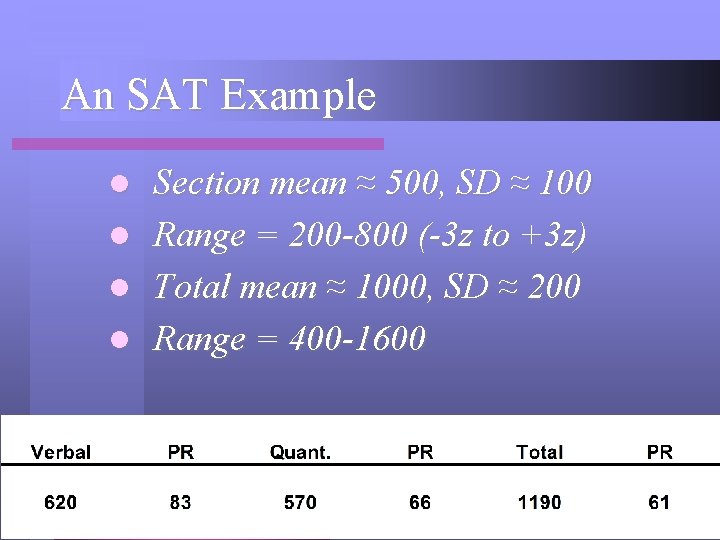
An SAT Example Section mean ≈ 500, SD ≈ 100 l Range = 200 -800 (-3 z to +3 z) l Total mean ≈ 1000, SD ≈ 200 l Range = 400 -1600 l

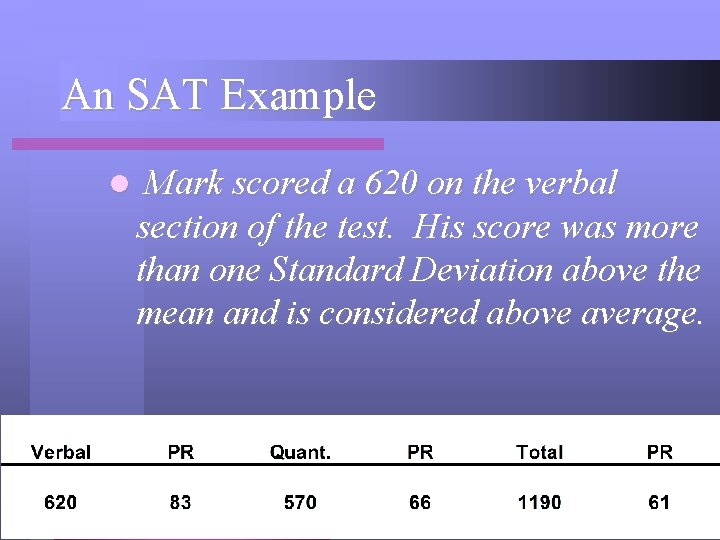
An SAT Example l Mark scored a 620 on the verbal section of the test. His score was more than one Standard Deviation above the mean and is considered above average.

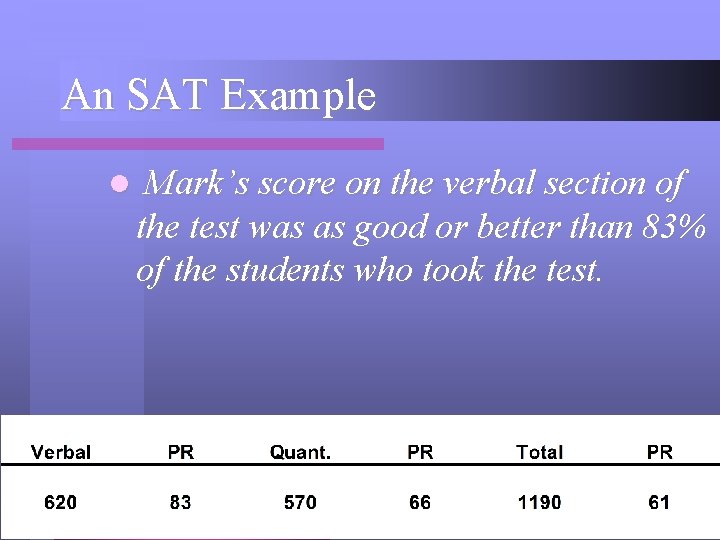
An SAT Example l Mark’s score on the verbal section of the test was as good or better than 83% of the students who took the test.

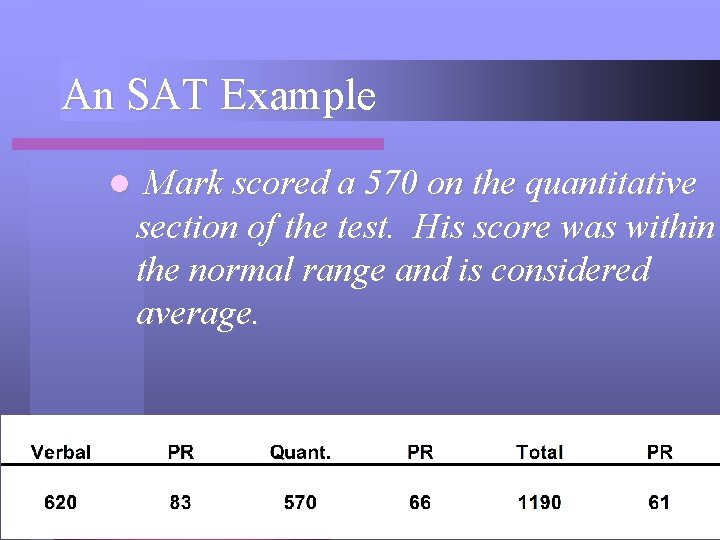
An SAT Example l Mark scored a 570 on the quantitative section of the test. His score was within the normal range and is considered average.

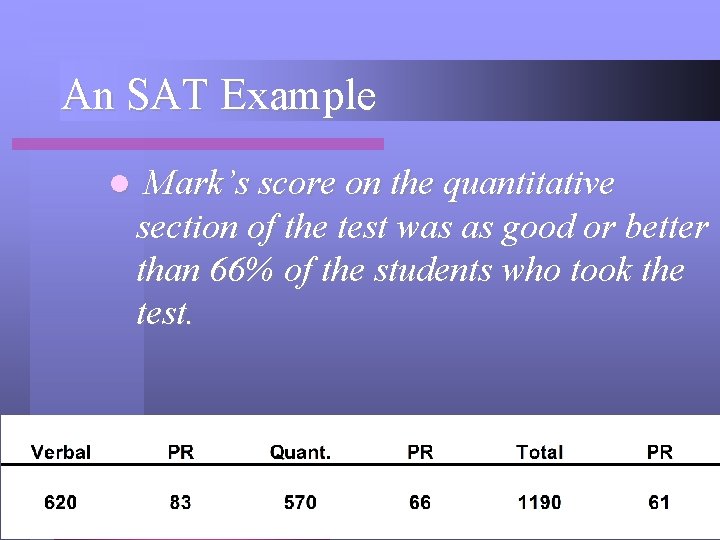
An SAT Example l Mark’s score on the quantitative section of the test was as good or better than 66% of the students who took the test.

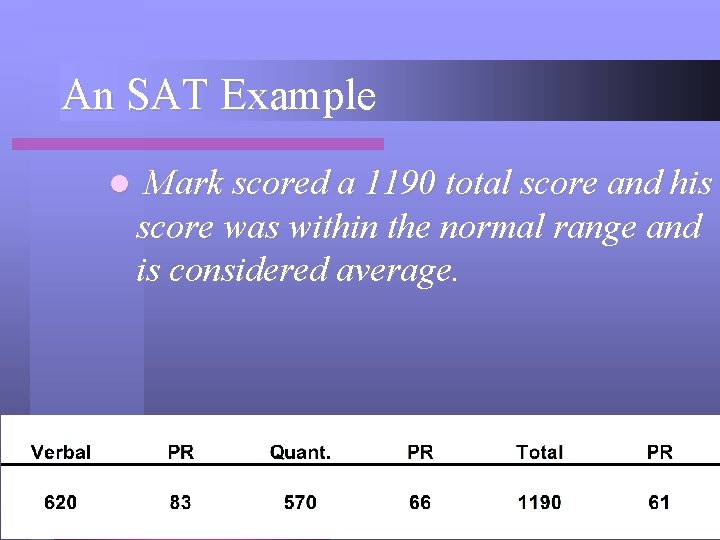
An SAT Example l Mark scored a 1190 total score and his score was within the normal range and is considered average.

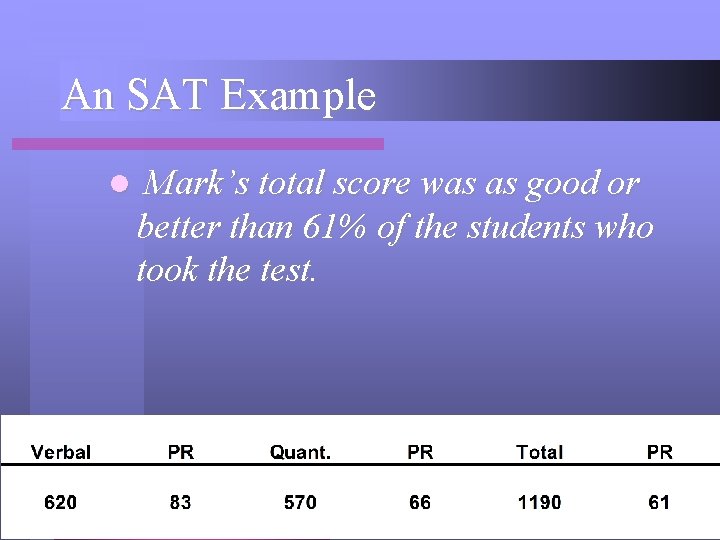
An SAT Example l Mark’s total score was as good or better than 61% of the students who took the test.

General Principles Tests do not measure innate ability l Test scores result from a combination of: l – Innate ability – Environmental influences – Test taker motivation – Properties of the test itself

Cautions about Interpretation l A low score in one norm group may be high in another, and vice versa. l A low score on one test will not necessarily lead to a high score on another test.

Cautions about Interpretation l Interpretation is part or clinical intuition and experience. l Become familiar with case studies in manuals.