STANDARDIZATION Direct Method Indirect Method 1 STANDARDIZATION Issue

STANDARDIZATION • Direct Method • Indirect Method 1

STANDARDIZATION Issue: Often times, we wish to compare mortality rates between populations, or at different time periods in one population, however, the population groups may differ with respect to underlying characteristics (e. g. age, gender) that may affect the overall mortality rate (hence – not a “fair” comparison). Standardization accounts for the differing distributions of the underlying characteristics 2

STANDARDIZATION Direct Standardization: “Adjusted” rates are derived by applying category-specific rates observed in each population to a single standard population. The “adjusted” rate represents the hypothetical rate that would have been observed had each population had the same distribution on the confounding factor of concern (i. e. age). 3

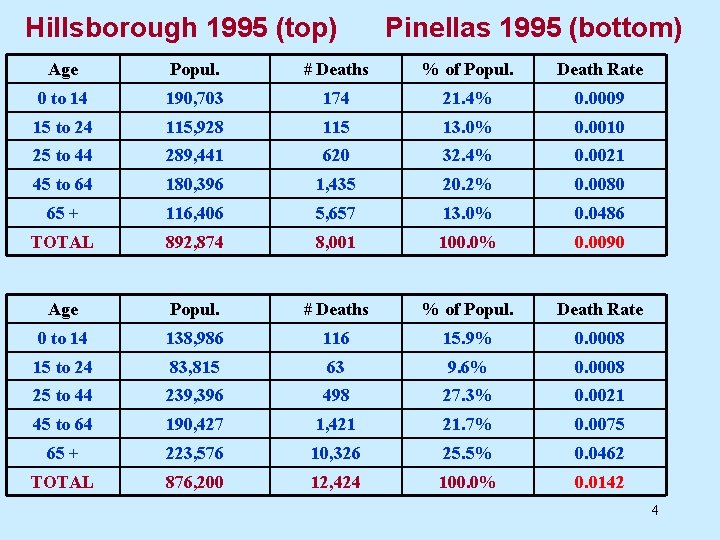
Hillsborough 1995 (top) Pinellas 1995 (bottom) Age Popul. # Deaths % of Popul. Death Rate 0 to 14 190, 703 174 21. 4% 0. 0009 15 to 24 115, 928 115 13. 0% 0. 0010 25 to 44 289, 441 620 32. 4% 0. 0021 45 to 64 180, 396 1, 435 20. 2% 0. 0080 65 + 116, 406 5, 657 13. 0% 0. 0486 TOTAL 892, 874 8, 001 100. 0% 0. 0090 Age Popul. # Deaths % of Popul. Death Rate 0 to 14 138, 986 116 15. 9% 0. 0008 15 to 24 83, 815 63 9. 6% 0. 0008 25 to 44 239, 396 498 27. 3% 0. 0021 45 to 64 190, 427 1, 421 21. 7% 0. 0075 65 + 223, 576 10, 326 25. 5% 0. 0462 TOTAL 876, 200 12, 424 100. 0% 0. 0142 4

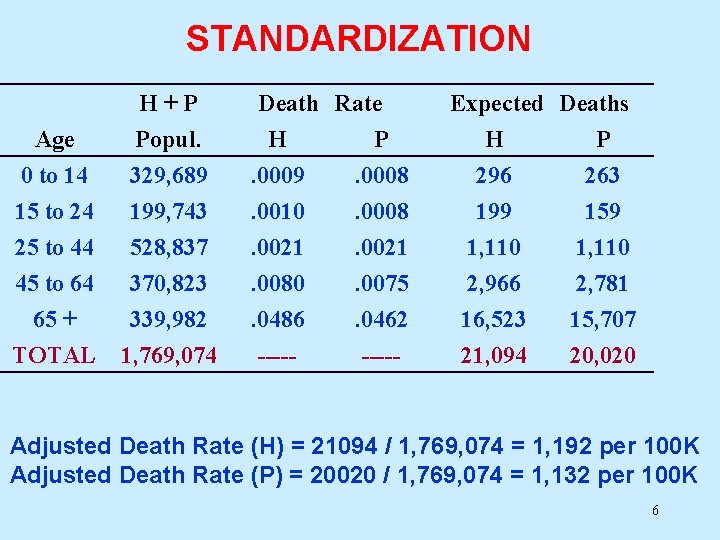
STANDARDIZATION Direct Standardization: One way to select the standard population is to combine population counts from the populations. We can then apply the category-specific death rates to the standard population to calculate and compare the expected number of deaths in each population. 5

STANDARDIZATION Age 0 to 14 15 to 24 H+P Popul. 329, 689 199, 743 25 to 44 45 to 64 65 + TOTAL 528, 837 370, 823 339, 982 1, 769, 074 Death Rate H P. 0009. 0008. 0010. 0008. 0021. 0080. 0486 ----- . 0021. 0075. 0462 ----- Expected Deaths H P 296 263 199 159 1, 110 2, 966 16, 523 21, 094 1, 110 2, 781 15, 707 20, 020 Adjusted Death Rate (H) = 21094 / 1, 769, 074 = 1, 192 per 100 K Adjusted Death Rate (P) = 20020 / 1, 769, 074 = 1, 132 per 100 K 6

STANDARDIZATION Adjusted Death Rate (H) = 21094 / 1, 769, 074 = 1, 192 per 100 K Adjusted Death Rate (P) = 20020 / 1, 769, 074 = 1, 132 per 100 K Age-adjusted rate ratio = 1, 192 / 1, 132 = 1. 05 Using Hillsborough + Pinellas county as the standard population: The age-adjusted 1995 death rate appears to be approximately 5% higher in Hillsborough county compared to Pinellas county. 7

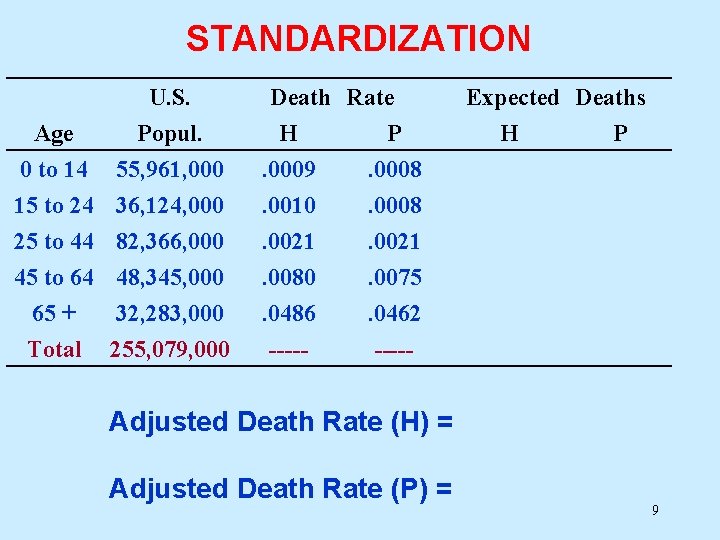
STANDARDIZATION Direct Standardization: Another way to select the standard population is to use an external standard population, such as the United States population. As before, we can then apply the categoryspecific death rates to the standard population to calculate and compare the expected number of deaths in each population. 8

STANDARDIZATION U. S. Age Popul. 0 to 14 55, 961, 000 15 to 24 36, 124, 000 Death Rate H P. 0009. 0008. 0010. 0008 25 to 44 45 to 64 65 + Total . 0021. 0080. 0486 ----- 82, 366, 000 48, 345, 000 32, 283, 000 255, 079, 000 Expected Deaths H P . 0021. 0075. 0462 ----- Adjusted Death Rate (H) = Adjusted Death Rate (P) = 9

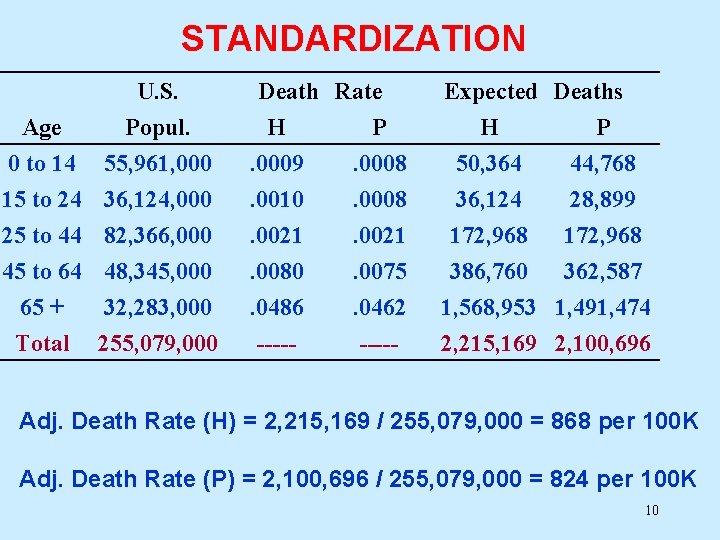
STANDARDIZATION U. S. Age Popul. 0 to 14 55, 961, 000 15 to 24 36, 124, 000 Death Rate H P. 0009. 0008. 0010. 0008 Expected Deaths H P 50, 364 44, 768 36, 124 28, 899 25 to 44 45 to 64 65 + Total . 0021. 0080. 0486 ----- 172, 968 386, 760 362, 587 1, 568, 953 1, 491, 474 2, 215, 169 2, 100, 696 82, 366, 000 48, 345, 000 32, 283, 000 255, 079, 000 . 0021. 0075. 0462 ----- Adj. Death Rate (H) = 2, 215, 169 / 255, 079, 000 = 868 per 100 K Adj. Death Rate (P) = 2, 100, 696 / 255, 079, 000 = 824 per 100 K 10

STANDARDIZATION Adj. Death Rate (H) = 2, 215, 169 / 255, 079, 000 = 868 per 100 K Adj. Death Rate (P) = 2, 100, 696 / 255, 079, 000 = 824 per 100 K Age-adjusted rate ratio = 868 / 824 = 1. 05 Using the United States as the standard population: The age-adjusted 1995 death rate appears to be approximately 5% higher in Hillsborough county compared to Pinellas county. 11

STANDARDIZATION Axioms (Direct Adjustment): 1. If the distribution of the population among the strata is the same for the two populations being compared, then adjustment is not needed. 2. If the distribution of the population among the strata is different for the two populations, adjustment is indicated (regardless of whether the stratum-specific rates are similar or different). 12

STANDARDIZATION Axioms (Direct Adjustment): 3. If the stratum-specific rates differ, calculating an adjusted rate will mask important differences. Thus, the adjusted rates should be compared cautiously, and the stratum-specific rates should be mentioned. 4. The selection of the standard population is arbitrary. However, when 2 or 3 populations are being compared, use the sum of the populations. 13

STANDARDIZATION Axioms (Direct Adjustment): 5. If you believe that one population is not exposed, and the other may be, choose the non-exposed group as the standard population. 6. You can choose a “standard” standard population: They usually come in sets of three: --- Developing World Standard – weighted to the young --- Developed World Standard – weighted to adults --- Global World Standard – average of the above two 14

STANDARDIZATION Reminders (Direct Adjustment): 1. Adjusted (standardized) rates are fictitious numbers. Their magnitude is related to the standard population chosen. 2. Adjusted rates should be used for comparison purposes only (i. e since they are hypothetical). 15

STANDARDIZATION Indirect Adjustment: 1. Conceptually similar to direct adjustment, but uses standard stratum-specific “rates” rather than standard stratum-specific “weights” (population counts). 2. Using the standard “rates, ” we compare the observed number of events to the expected number of events. 16

STANDARDIZATION Indirect Adjustment: THE RESULTS ARE PRESENTED AS THE “STANDARDIZED MORBIDITY” OR “MORTALITY” RATIO (SMR) SMR = observed cases (O) ------------ ( x 100) expected cases (E) 17

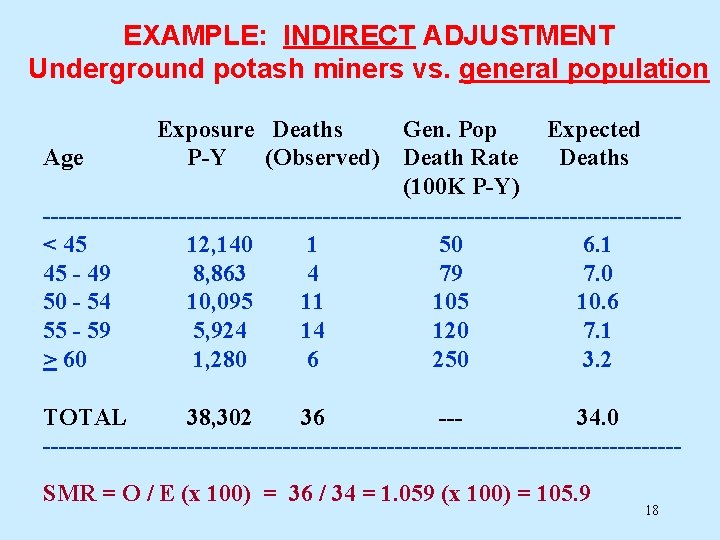
EXAMPLE: INDIRECT ADJUSTMENT Underground potash miners vs. general population Exposure Deaths Gen. Pop Expected Age P-Y (Observed) Death Rate Deaths (100 K P-Y) ----------------------------------------< 45 12, 140 1 50 6. 1 45 - 49 8, 863 4 79 7. 0 50 - 54 10, 095 11 105 10. 6 55 - 59 5, 924 14 120 7. 1 > 60 1, 280 6 250 3. 2 TOTAL 38, 302 36 --34. 0 ----------------------------------------SMR = O / E (x 100) = 36 / 34 = 1. 059 (x 100) = 105. 9 18

EXAMPLE: INDIRECT ADJUSTMENT Underground potash miners vs. general population Interpretation: SMR = 105. 9 We estimate that underground potash miners have a 6% higher risk of mortality than the general population. 19

EXAMPLE: INDIRECT ADJUSTMENT Underground potash miners vs. general population Interpretation: SMR = 105. 9 But don’t forget about the “healthy worker” effect (e. g. we expect workers to have a lower mortality than the general population). Also, beware that the general population almost always contains some exposed individuals (e. g. bias toward the null). 20

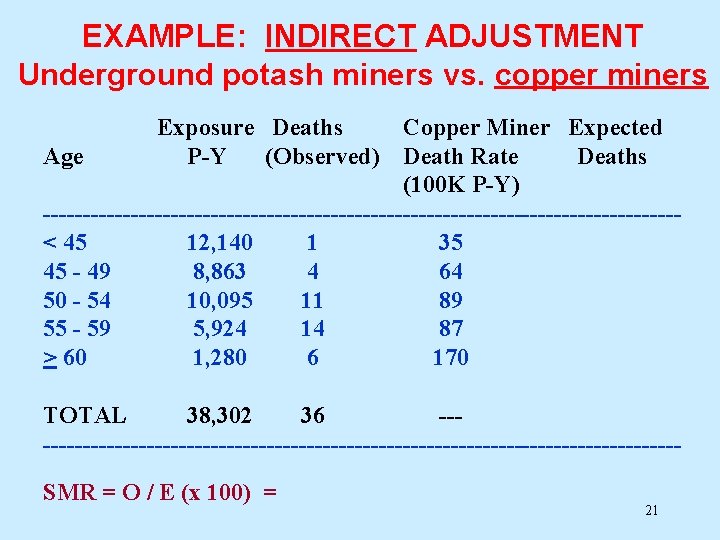
EXAMPLE: INDIRECT ADJUSTMENT Underground potash miners vs. copper miners Exposure Deaths Copper Miner Expected Age P-Y (Observed) Death Rate Deaths (100 K P-Y) ----------------------------------------< 45 12, 140 1 35 45 - 49 8, 863 4 64 50 - 54 10, 095 11 89 55 - 59 5, 924 14 87 > 60 1, 280 6 170 TOTAL 38, 302 36 -----------------------------------------SMR = O / E (x 100) = 21

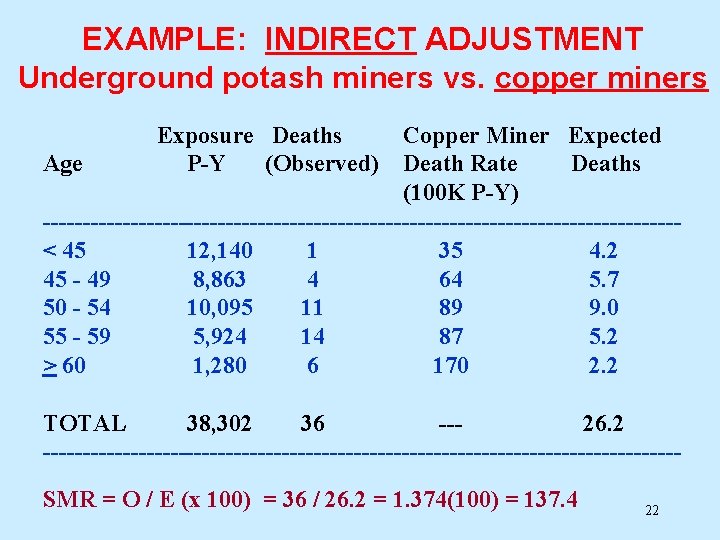
EXAMPLE: INDIRECT ADJUSTMENT Underground potash miners vs. copper miners Exposure Deaths Copper Miner Expected Age P-Y (Observed) Death Rate Deaths (100 K P-Y) ----------------------------------------< 45 12, 140 1 35 4. 2 45 - 49 8, 863 4 64 5. 7 50 - 54 10, 095 11 89 9. 0 55 - 59 5, 924 14 87 5. 2 > 60 1, 280 6 170 2. 2 TOTAL 38, 302 36 --26. 2 ----------------------------------------SMR = O / E (x 100) = 36 / 26. 2 = 1. 374(100) = 137. 4 22

EXAMPLE: INDIRECT ADJUSTMENT Underground potash miners vs. copper miners Interpretation: SMR = 137. 4 We estimate that underground potash miners have a 37% higher risk of mortality than copper miners. 23

STANDARDIZATION Axioms (Indirect Adjustment): 1. It is usually not appropriate to compare a number of SMRs from different study populations with each other. This is because the distribution of exposure among the strata (i. e. person years of followup) will usually be different for each study population. Thus, the standard rates are not being applied to standard weights. 24

STANDARDIZATION Axioms (Indirect Adjustment): 2. Direct standardization is preferred over indirect standardization. Still, indirect standardization: • Has been traditionally used in public health • Has intuitive appeal and is easy to understand • Works well almost all of the time -- despite not guaranteeing standardization • Is well known by journal editor and readers 25