Standard Position Coterminal and Reference Angles Measure of

Measure of an Angle 1 -1 Initial Side n i m er T e

Coterminal Angles 1 Angles that share the same initial and terminal sides. -1 1

Coterminal Angles that have the same initial and terminal sides are coterminal. Angles and

Example of Finding Coterminal Angles You can find an angle that is coterminal to

Ex 2. Find one positive and one negative angle that is coterminal with the

Ex 4. Find one positive and one negative angle that is coterminal with the

Reference Angles The values of the trigonometric functions of angles greater than 90 (or

Reference Angles The reference angles for in Quadrants II, III, and IV are shown

Example – Finding Reference Angles Find the reference angle ′. a. = 300 b.

Example (a) – Solution Because 300 lies in Quadrant IV, the angle it makes

Example (b) – Solution Because 2. 3 lies between /2 1. 5708 and 3.

Example (c) – Solution First, determine that – 135 is coterminal with 225 ,

Reference Angles When your angle is negative or is greater than one revolution, to

Your Turn: Find the reference angle for each of the following. 1. 213° 2.

Slides: 16

Download presentation

Standard Position, Coterminal and Reference Angles

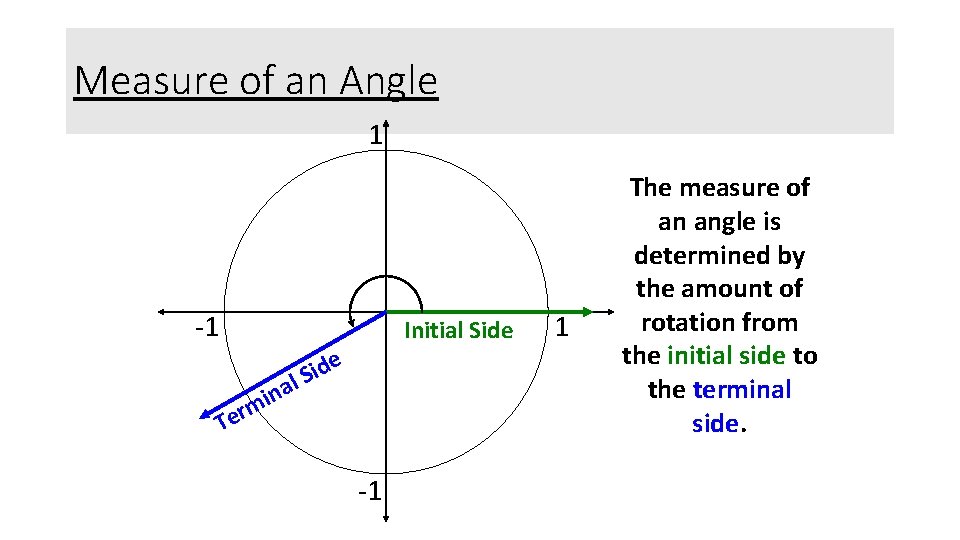
Measure of an Angle 1 -1 Initial Side n i m er T e d i al S -1 1 The measure of an angle is determined by the amount of rotation from the initial side to the terminal side.

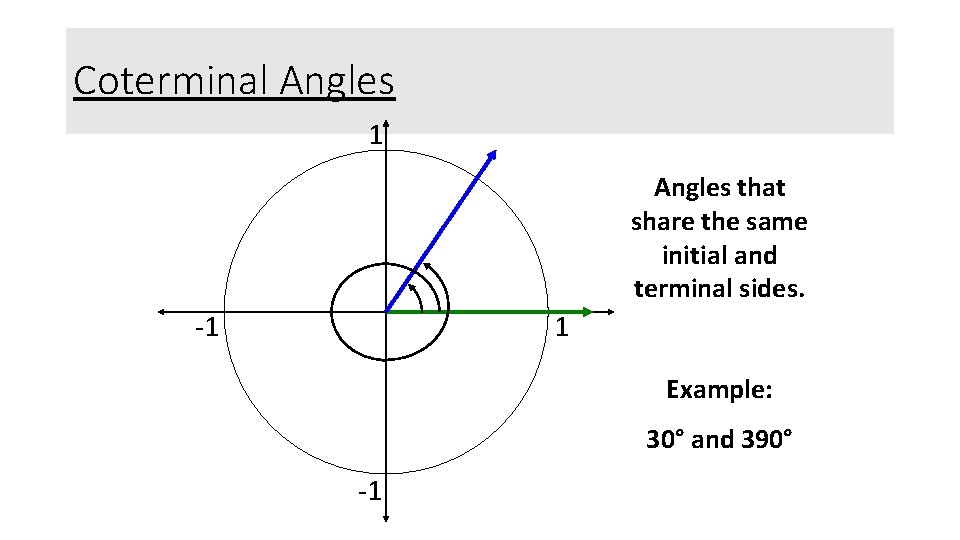
Coterminal Angles 1 Angles that share the same initial and terminal sides. -1 1 Example: 30° and 390° -1

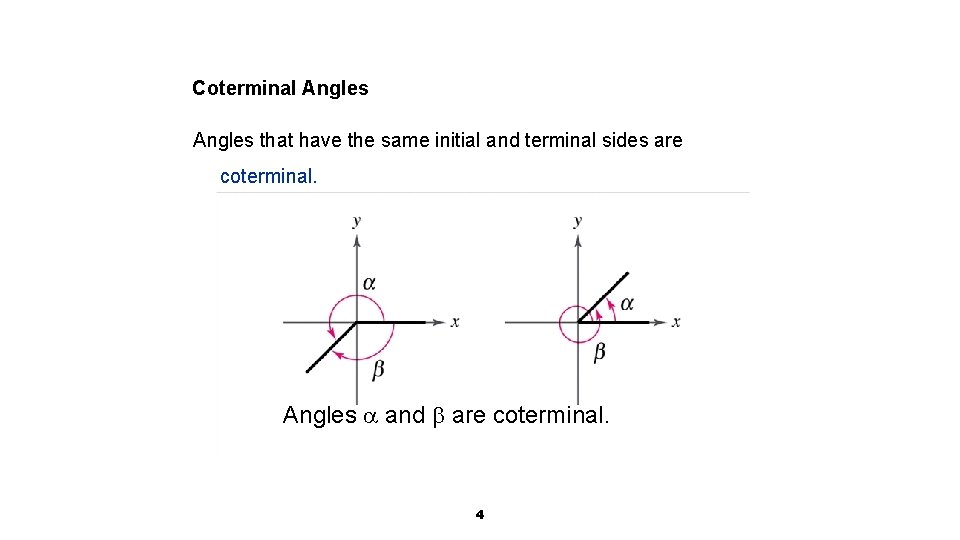
Coterminal Angles that have the same initial and terminal sides are coterminal. Angles and are coterminal. 4

Example of Finding Coterminal Angles You can find an angle that is coterminal to a given angle by adding or subtracting multiples of 360º. Ex 1: Find one positive and one negative angle that are coterminal to 112º. For a positive coterminal angle, add 360º : 112º + 360º = 472º For a negative coterminal angle, subtract 360º: 112º - 360º = -248º 5

Ex 2. Find one positive and one negative angle that is coterminal with the angle = 30° in standard position. Ex 3. Find one positive and one negative angle that is coterminal with the angle = 272 in standard position.

Ex 4. Find one positive and one negative angle that is coterminal with the angle = in standard position. Ex 5. Find one positive and one negative angle that is coterminal with the angle = in standard position.

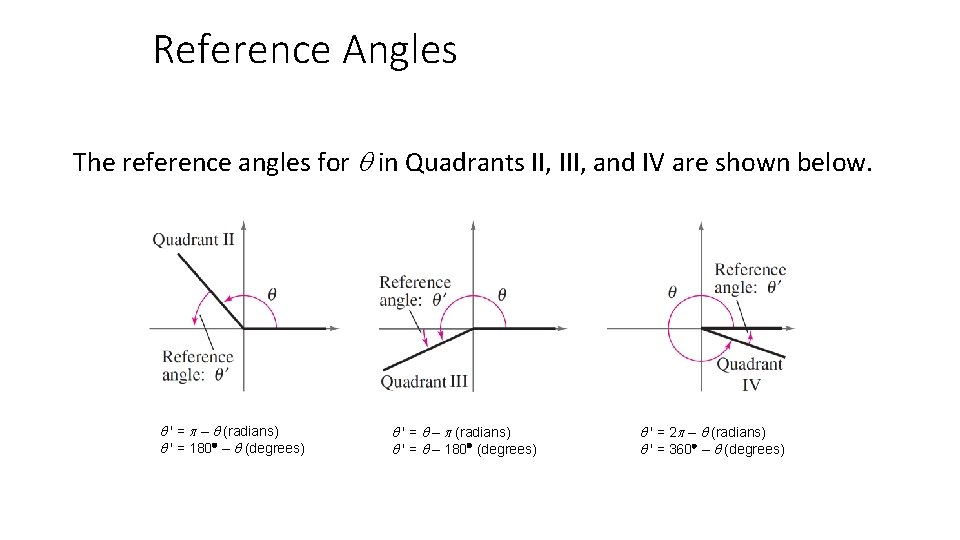
Reference Angles The values of the trigonometric functions of angles greater than 90 (or less than 0 ) can be determined from their values at corresponding acute angles called reference angles. �� ’ ��

Reference Angles The reference angles for in Quadrants II, III, and IV are shown below. ′ = – (radians) ′ = 180 – (degrees) ′ = – (radians) ′ = – 180 (degrees) ′ = 2 – (radians) ′ = 360 – (degrees)

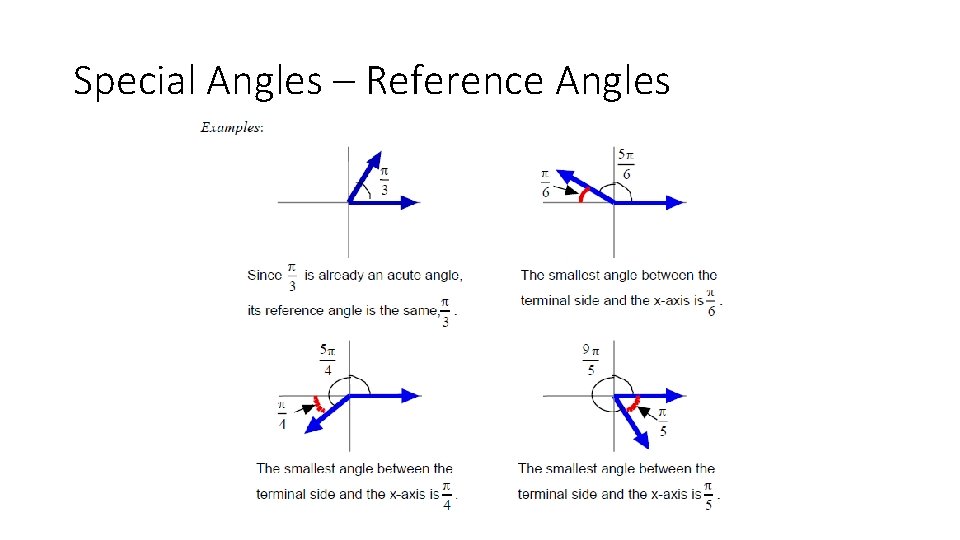
Special Angles – Reference Angles

Example – Finding Reference Angles Find the reference angle ′. a. = 300 b. = 2. 3 c. = – 135

Example (a) – Solution Because 300 lies in Quadrant IV, the angle it makes with the x-axis is ′ = 360 – 300 Degrees = 60. The figure shows the angle = 300 and its reference angle ′ = 60.

Example (b) – Solution Because 2. 3 lies between /2 1. 5708 and 3. 1416, it follows that it is in Quadrant II and its reference angle is ′ = – 2. 3 Radians 0. 8416. The figure shows the angle = 2. 3 and its reference angle ′ = – 2. 3. cont’d

Example (c) – Solution First, determine that – 135 is coterminal with 225 , which lies in Quadrant III. So, the reference angle is ′ = 225 – 180 = 45. The figure shows the angle = – 135 and its reference angle ′ = 45. Degrees cont’d

Reference Angles When your angle is negative or is greater than one revolution, to find the reference angle, first find the positive coterminal angle between 0° and 360° or 0 and 2��.

Your Turn: Find the reference angle for each of the following. 1. 213° 2. 1. 7 3. − 144° -144 is coterminal to 216 - 180 = 36