Standard Model Lesson 2 Asymmetry measurements and global

Standard Model Lesson #2 Asymmetry measurements and global fit Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

Forward-backward asymmetries f e- e+ _ f Backward Forward Asymmetric term Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

e+ e+ g(s) e- Z(s) e- te t n s m r a in m Do Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

G 1(s) G 3(s) For s ~ MZ 2 I can consider only the dominant terms Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

The cross section can be expressed as a function of the forward-backward asymmetry Considering only the dominant terms the asymmetric contribution to the cross section is the product Ae Af Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

The forward-backward asymmetry can be measured with the counting method: or using the “maximum likelihood fit” method: With the counting method we do not assume theoretical distribution With the likelihood method the statistical error is lower Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

0. 95 Ad 0. 70 Au 0. 15 Ae 0. 23 0. 24 0. 25 sin 2 W At the tree level the forward-backward asymmetry it’s simply related to the sin 2 W value and to the fermion final state. AFB measurement for different f comparison between different sin 2 W estimation Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

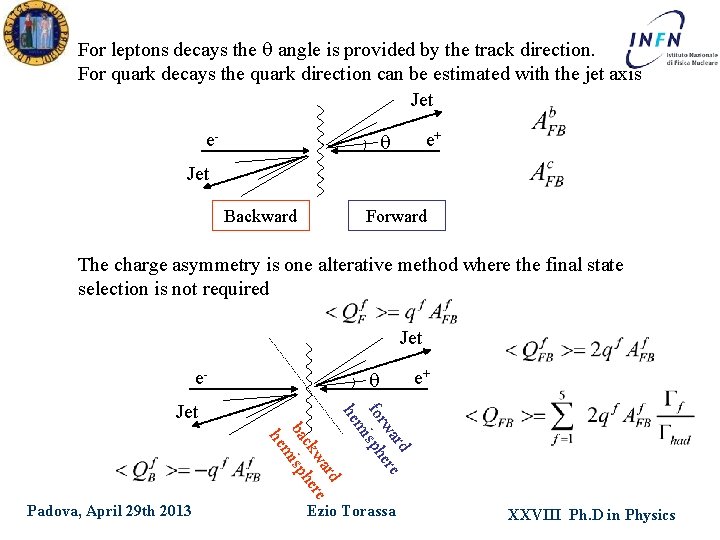
For leptons decays the angle is provided by the track direction. For quark decays the quark direction can be estimated with the jet axis Jet e- e+ Jet Backward Forward The charge asymmetry is one alterative method where the final state selection is not required Jet e- e+ rd wa re ck he ba isp m he ard e rw er fo isph m he Jet Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

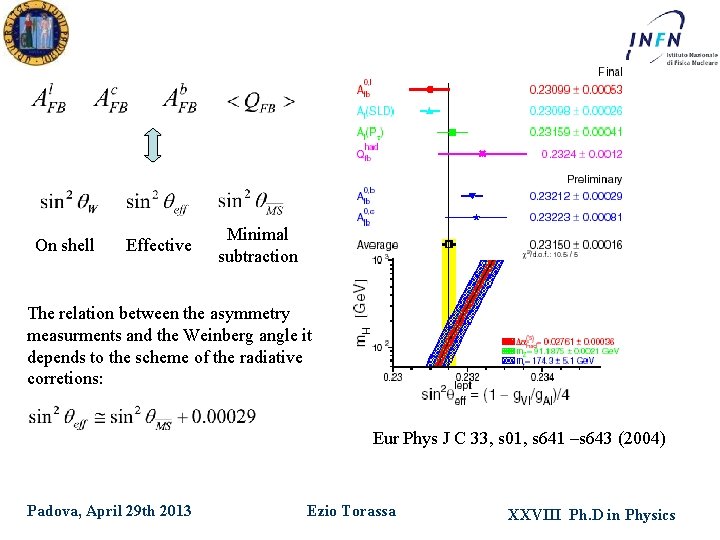
On shell Effective Minimal subtraction The relation between the asymmetry measurments and the Weinberg angle it depends to the scheme of the radiative corretions: Eur Phys J C 33, s 01, s 641 –s 643 (2004) Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

sin 2 eff. W and radiative corrections We considered the following 3 parameters for the QEWD : sin W GF A better choice are the physical quantities we can measure with high precision: measured with anomalous magnetic dipole moment of the electron GF measured with the lifetime of the muon MZ measured with the line shape of the Z sin W e MW becomes derived quantities related to mt e m. H. The Weinberg angle can be defined with different relations. They are equivalent at the tree level but different when the radiative corrections are considered: (1) (2) (On shell) Padova, April 29 th 2013 (NOV) Ezio Torassa XXVIII Ph. D in Physics

Starting with the on-shell definition, including the radiative corerctions, we have: EW loops EW vertex H r = We can avoid to apply corrections related to mt m. H in the final result simply defining the Weinberg angle in the “effective scheme” Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

Final Weinberg angle measurement: sin 2 eff=0. 23150± 0. 00016 P( 2)=7% (10. 5/5) 0. 23113 ± 0. 00020 leptons 0. 23213 ± 0. 00029 hadrons Larger discrepancy: Al(SLD) –Afbb Padova, April 29 th 2013 Ezio Torassa 2. 9 XXVIII Ph. D in Physics

s m er t t AFB function of s n a in m Do Outside the Z 0 peak the terms with the function | 0(s)|2 are not anymore dominant, they became negligible. The function Re( 0(s)) can be simplified 0 s 0 Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

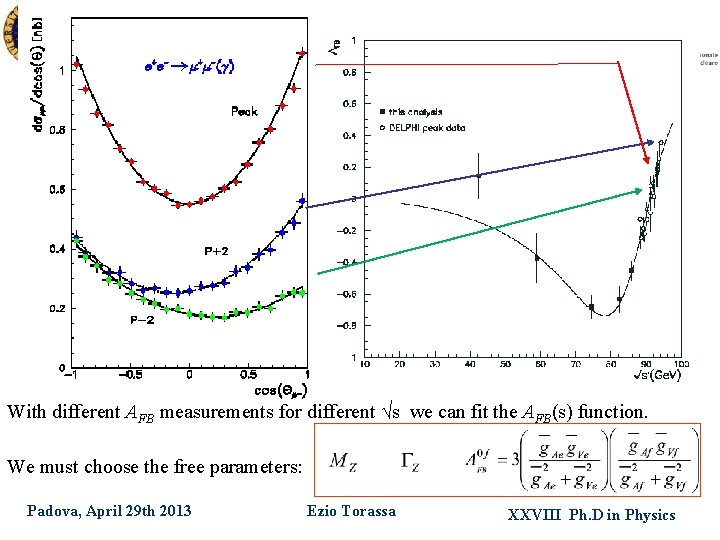
With different AFB measurements for different √s we can fit the AFB(s) function. We must choose the free parameters: Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

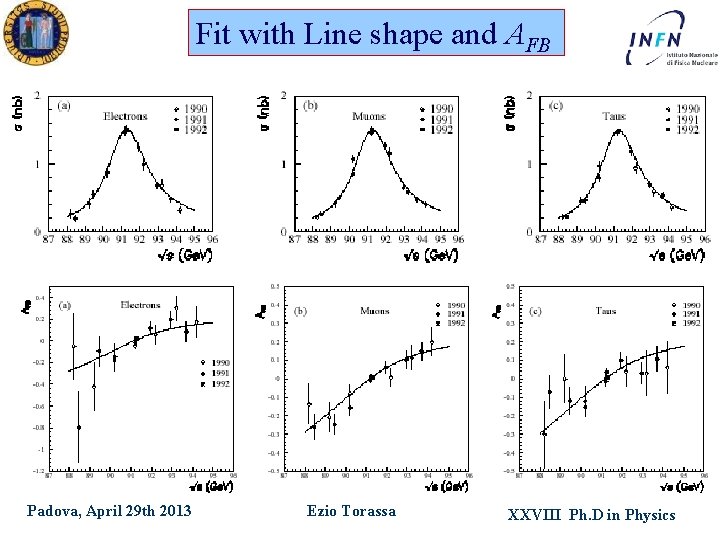
Fit with Line shape and AFB Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

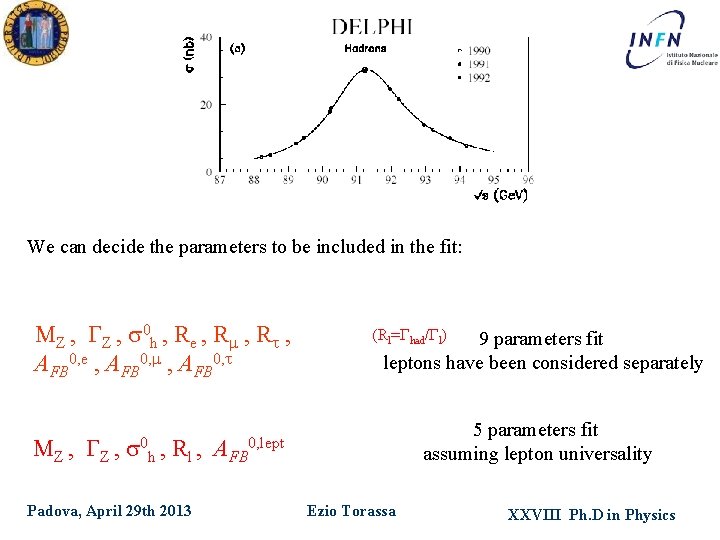
We can decide the parameters to be included in the fit: MZ , GZ , s 0 h , Re , Rm , Rt , AFB 0, e , AFB 0, m , AFB 0, t (Rl=Ghad/Gl) 9 parameters fit leptons have been considered separately 5 parameters fit assuming lepton universality MZ , GZ , s 0 h , Rl , AFB 0, lept Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

Lepton universality The coupling constants between Z and fermions are identical in the SM. We can check this property with the real data. g. V and g. A for different fermions are compatible within errors Error contributions due to: - MH , Mtop - theoretical incertanty on QED(MZ 2) Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

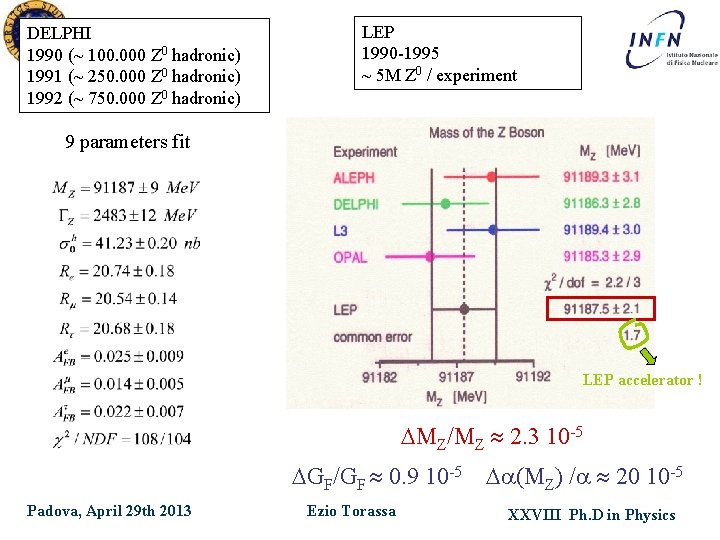
DELPHI 1990 (~ 100. 000 Z 0 hadronic) 1991 (~ 250. 000 Z 0 hadronic) 1992 (~ 750. 000 Z 0 hadronic) LEP 1990 -1995 ~ 5 M Z 0 / experiment 9 parameters fit LEP accelerator ! MZ/MZ 2. 3 10 -5 GF/GF 0. 9 10 -5 Padova, April 29 th 2013 Ezio Torassa (MZ) / 20 10 -5 XXVIII Ph. D in Physics

t polarization measurement from Z tt Z bosons produced with unpolarized beams are polarized due to parity violation t from Z decay are polarized, we can measure Pt from the t decays. t rest frame n p- * t- t spin In the case of a t decaying to a pion and a neutrino, the neutrino is preferably emitted opposite the spin orientation of the t to conserve angular momentum, this is due to the left-handed nature of the neutrino. Hence, the pion will preferably be emitted in the direction of the spin orientation of the t. * is defined to be the angle in the rest frame of the t lepton between the direction of the t and the direction of the pion. The distribution of * is related to Pt : Padova, April 29 th background 2013 Ezio Torassa XXVIII Ph. D in Physics

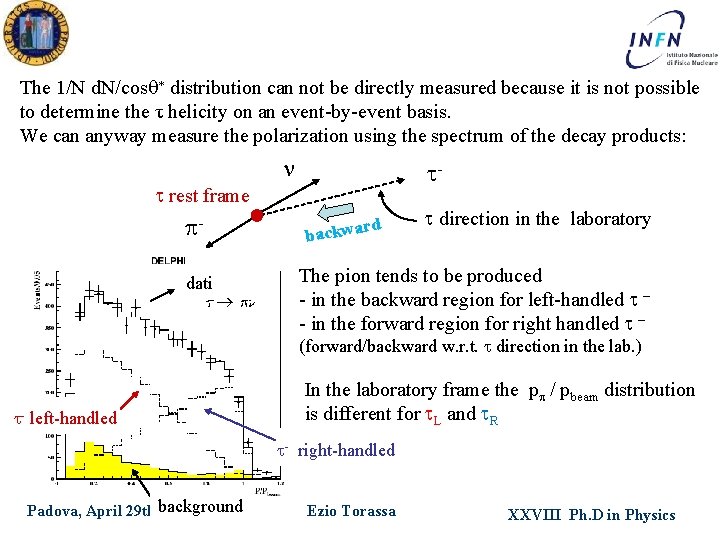
The 1/N d. N/cos * distribution can not be directly measured because it is not possible to determine the τ helicity on an event-by-event basis. We can anyway measure the polarization using the spectrum of the decay products: n t- t rest frame pdati rd backwa t direction in the laboratory The pion tends to be produced - in the backward region for left-handled t – - in the forward region for right handled t – (forward/backward w. r. t. t direction in the lab. ) t- left-handled In the laboratory frame the pp / pbeam distribution is different for t. L and t. R t- right-handled Padova, April 29 th background 2013 Ezio Torassa XXVIII Ph. D in Physics

The pp / pbeam distribution is related to the t polarization: The t polarization can be measured observing the final state particle distributions for different decays : t pn t 3 pn t rn t mnn, enn In case of a leptonic decay the presence of two neutrinos in the final state makes this channel less sensitive to the tau helicity: t- left-handled Padova, April 29 th 2013 t- right-handled Ezio Torassa XXVIII Ph. D in Physics

The polarization is measured in several bin of the polar angle cos Q between the pion and the beam direction (within 3° is a good approximation of the angle between t and beam direction) Fit: Compared with At. FB = ¾ Ae At Pt (cos Q) provides one independent measurement of Ae e At Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

Misura della polarizzazione Utilizza lo scattering Compton della luce polarizzata. L’angolo di scattering dipendente dallo spin dell’elettrone. • Compton Polarimeter <Pe-> = 75 % σ<Pe> = 0. 5 % • Quartz Fiber Polarimeter and Polarized Gamma Counter – run on single e- beam + crosschecks • <Pe+> = -0. 02 ± 0. 07 % elettroni diffusi Luce polarizzata Circolarmente (YAG Laser, 532 nm) Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

Left-Right asymmetry at SLD With polarized beam we can measure the Left-Right asymmetry: Cross section with ‘left-handed’ polarized beam: e. L-e+ ff ( Pe = 1 ) Cross section with ‘right-handed’ polarized beam: e. R-e+ ff To estimate the cross section difference betwnn e-L e+ and e-R e+ we need a very precise luminosity control. The e- beam polarization was inverted at SLC at the crossing frequncy (120 Hz) to have the same luminosity for e. L and e. R with Pe < 1 we measure only : Am. LR = (NL-NR) / (NL+NR) the left-right asymmetry is given by: precise measurement Pe is needed ALR = Am. LR / Pe Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

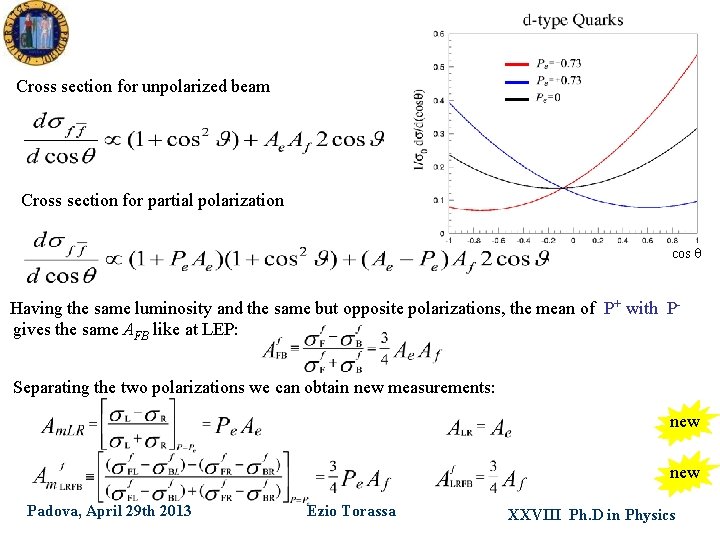
Cross section for unpolarized beam Cross section for partial polarization cos Having the same luminosity and the same but opposite polarizations, the mean of P+ with Pgives the same AFB like at LEP: Separating the two polarizations we can obtain new measurements: new Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

Asymmetry results at SLD • Af with ALRFB • Combined with Ae from ALR With only 1/10 of statistics, thanks to the beam polarization, SLD was competitive with LEP for the Weinberg angle measurement: SLD LEPleptons Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

Global Electroweak Fit From the experimental observables: line shape s(s) FB asymmetries AFB(s) t polarization Pt(cos ) pseudo-osservables can be extrapolated: MZ GZ s 0 h Al. FB etc. . Using a fit program (ZFITTER) with 2 loop QEWD and 3 loop QED the best fit can be obtained for the parameters of the model and for the masses having some uncertainty (mt, , m. H ). The current version of ZFITTER (in C++) is Gfitter. Global fits are performed in two versions: the standard fit uses all the available informations except results from direct Higgs searches, the complete fit includes everything Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

20 pseudo-osservables 5 fitted parameters With the fitted parameters we can obtain also the fitted pseudo-osservables Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

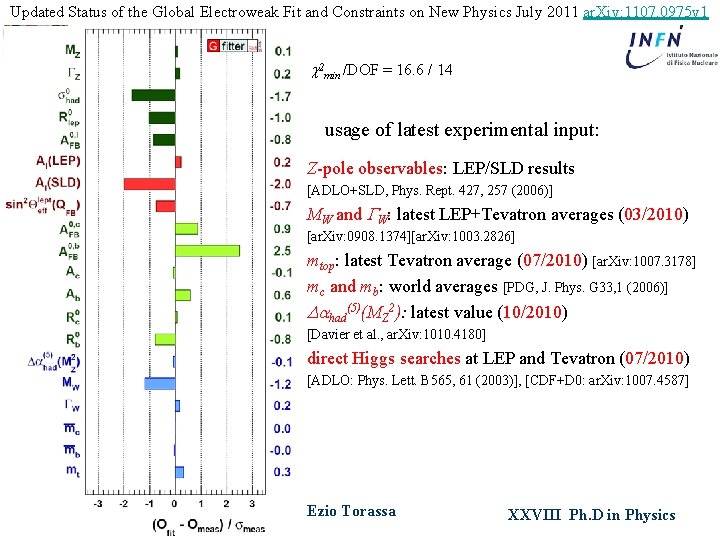
Updated Status of the Global Electroweak Fit and Constraints on New Physics July 2011 ar. Xiv: 1107. 0975 v 1 c 2 min /DOF = 16. 6 / 14 usage of latest experimental input: Z-pole observables: LEP/SLD results [ADLO+SLD, Phys. Rept. 427, 257 (2006)] MW and GW: latest LEP+Tevatron averages (03/2010) [ar. Xiv: 0908. 1374][ar. Xiv: 1003. 2826] mtop: latest Tevatron average (07/2010) [ar. Xiv: 1007. 3178] mc and mb: world averages [PDG, J. Phys. G 33, 1 (2006)] Dahad(5)(MZ 2): latest value (10/2010) [Davier et al. , ar. Xiv: 1010. 4180] direct Higgs searches at LEP and Tevatron (07/2010) [ADLO: Phys. Lett. B 565, 61 (2003)], [CDF+D 0: ar. Xiv: 1007. 4587] Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics

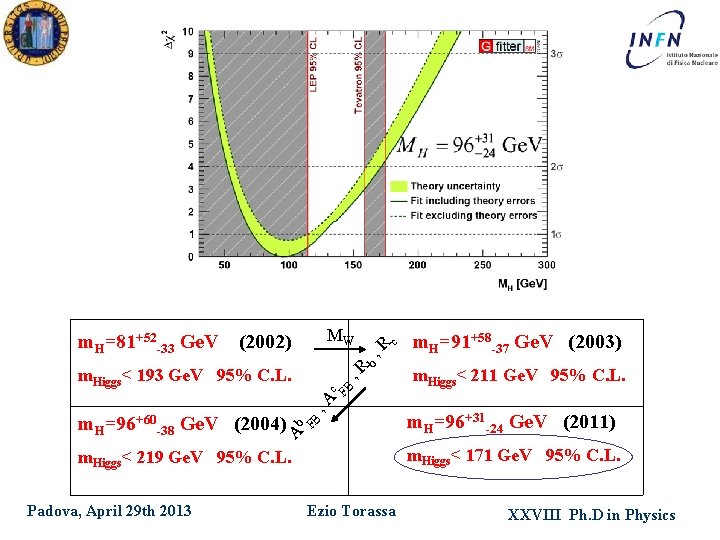
c b Ab FB , A c FB m. Higgs< 193 Ge. V 95% C. L. m. H=96+60 -38 Ge. V (2004) , R MW (2002) , R m. H=81+52 -33 Ge. V m. Higgs< 211 Ge. V 95% C. L. m. H=96+31 -24 Ge. V (2011) m. Higgs< 171 Ge. V 95% C. L. m. Higgs< 219 Ge. V 95% C. L. Padova, April 29 th 2013 m. H=91+58 -37 Ge. V (2003) Ezio Torassa XXVIII Ph. D in Physics

Z Physics at LEP I CERN 89 -08 Vol 1 – Forward-backward asymmetries (pag. 203) Measurement of the lineshape of the Z and determination of electroweak parameters from its hadronic decays - Nuclear Physics B 417 (1994) 3 -57 Improved measurement of cross sections and asymmetries at the Z resonance - Nuclear Physics B 418 (1994) 403 -427 Global fit to electroweak precision data Eur. Phys J C 33, s 01, s 641 –s 643 (2004) Measurement of the t polarization in Z decays – Z. Phys. C 67 183 -201 (1995) Padova, April 29 th 2013 Ezio Torassa XXVIII Ph. D in Physics