Standard deviation Continuous series Actual Mean MethodDirect Method

Standard deviation Continuous series

Actual Mean Method/Direct Method Continuous Series Steps : 1. Ascertain mid points (m) and multiply it by frequency to obtain - fm. Now apply the formula Σfm/N to find out mean. 2. Calculate deviations from mean and denote as –d 3. Deviations and frequency should be multiplied to determine fd. 4. Multiply d and fd to obtain fd 2. 2 5. Find the aggregate of fd & fd 2 and express them as Σfd & Σfd. 6. Now apply the formula : 2 Σfd ___ N Example : Calculate the standard deviation and its co-efficient from the following : Size Frequency 0. 5 - 1. 5 1 1. 5 – 4. 5 2 4. 5 – 5. 5 3 5. 5 – 8. 5 4 8. 5 – 13. 5 5

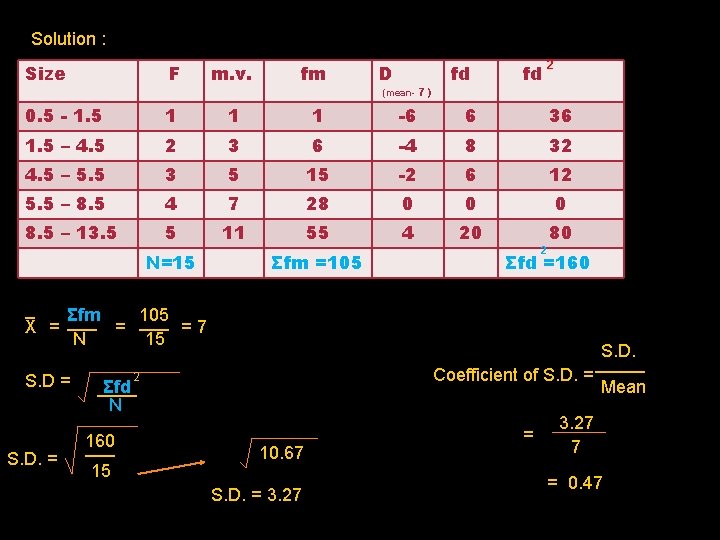
Solution : F m. v. fm 0. 5 - 1. 5 1 1 1 -6 6 36 1. 5 – 4. 5 2 3 6 -4 8 32 4. 5 – 5. 5 3 5 15 -2 6 12 5. 5 – 8. 5 4 7 28 0 0 0 8. 5 – 13. 5 5 11 55 4 20 80 N=15 Σfm =105 _ Σfm 105 X = ___ = 7 N 15 S. D = S. D. = (mean- 7 ) fd fd 2 Σfd =160 S. D. _____ Coefficient of S. D. = Mean 2 ____ Σfd N 160 ___ 15 D 2 Size 10. 67 S. D. = 3. 27 7 = 0. 47

Standard Deviation in Continuous Series Assumed Mean Method Or Short cut Method Steps : 1. Find out value from the class interval and express it by M 2. Assume mean and calculate deviations from it. Denote with ‘d’ 3. Multiply deviation by frquency and obtain fd. 4. Multiply fd by d and obtain fd 5. Find Σfd & Σfd 2 2 Apply the following formula : Σfd 2 - ___ Σfd N 2 N Example : Calculate SD from the following frequency distribution. using A. Mean method Age in years : No. of employees 18 -28 28 -38 5 8 38 -48 10 48 -58 7

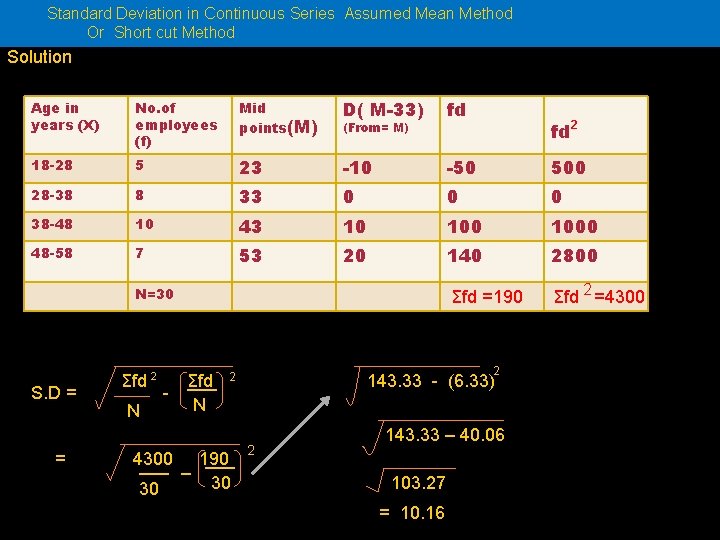
Standard Deviation in Continuous Series Assumed Mean Method Or Short cut Method Solution Age in years (X) No. of employees (f) Mid points(M) D( M-33) fd 18 -28 5 23 -10 -50 500 28 -38 8 33 0 0 0 38 -48 10 43 10 1000 48 -58 7 53 20 140 2800 Σfd =190 Σfd 2 =4300 (From= M) N=30 S. D = = Σfd 2 N - ___ Σfd N 2 2 4300 ___ _ 190 30 30 fd 2 143. 33 - (6. 33) 2 143. 33 – 40. 06 103. 27 = 10. 16

Standard deviation –steps (continuous series) • Step 1: Find the mid points of various classes • Step 2: Take the deviations of these mid points from assumed mean and denote these deviations by ‘d’ • Step 3: Take a common factor and denote this column by d • Step 4: Multiply the frequencies of each class with the deviations and obtain ∑fd • Step 5: Square the deviations and multiply with the respective frequencies of each class and obtain ∑fd 2 • Thus the only difference in procedure in continuous series is to find the mid- points of various classes.

Standard deviation step deviation method (continuous series) • In continuous series any of the three methods can be used. The formula for the step deviation method is σ= Where d = A =Assumed mean i = class interval m=mid points

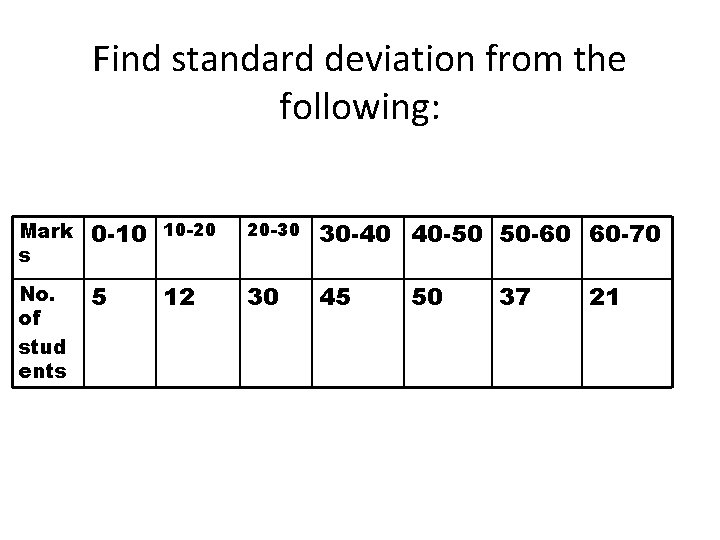
Find standard deviation from the following: Mark s 0 -10 10 -20 20 -30 30 -40 40 -50 50 -60 60 -70 No. of stud ents 5 12 30 45 50 37 21

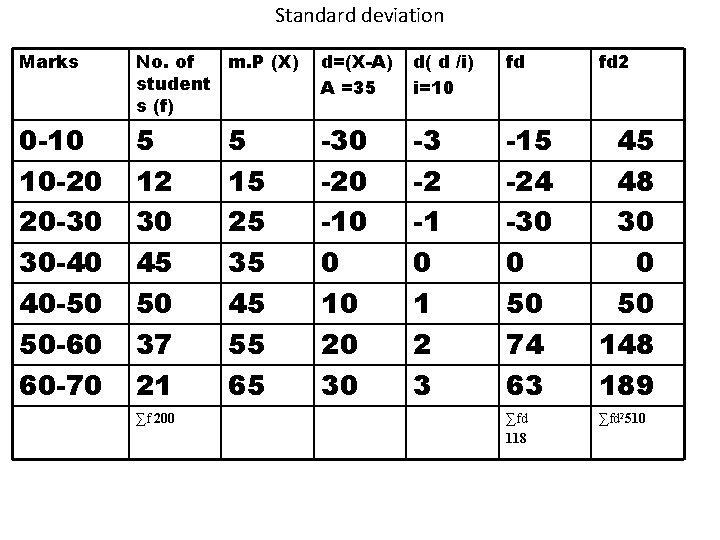
Standard deviation Marks No. of m. P (X) student s (f) d=(X-A) A =35 d( d /i) i=10 fd fd 2 0 -10 10 -20 20 -30 30 -40 40 -50 50 -60 60 -70 5 12 30 45 50 37 21 -30 -20 -10 0 10 20 30 -3 -2 -1 0 1 2 3 -15 -24 -30 0 50 74 63 45 48 30 0 50 148 189 ∑fd 118 ∑fd 2510 ∑f 200 5 15 25 35 45 55 65

Standard deviation continuous series- Solution • σ = Hide Next

2. 55 - (0. 59) 2 2. 55 - 0. 34 x 10 2. 21 x 10 = 1. 48 x 10 = 14. 8 X 10

Merits and demerits of standard deviation • Merits: • It is based on all values. • It is amenable to further algebraic treatment. • It is less affected by fluctuations of sampling than any other measures of dispersion. Demerits: It is difficult to compute. In the calculation of standard deviation extreme values from mean are given more importance than the values near the mean.