Standard Cases for Slope and Deflection SSB Lecture

Standard Cases for Slope and Deflection (SSB) Lecture No-3 J P Supale Mechanical Engineering Department SKN SITS LONAVALA Strength of Materials

Standard Cases • SSB with point loads • SSB with UDL Strength of Materials

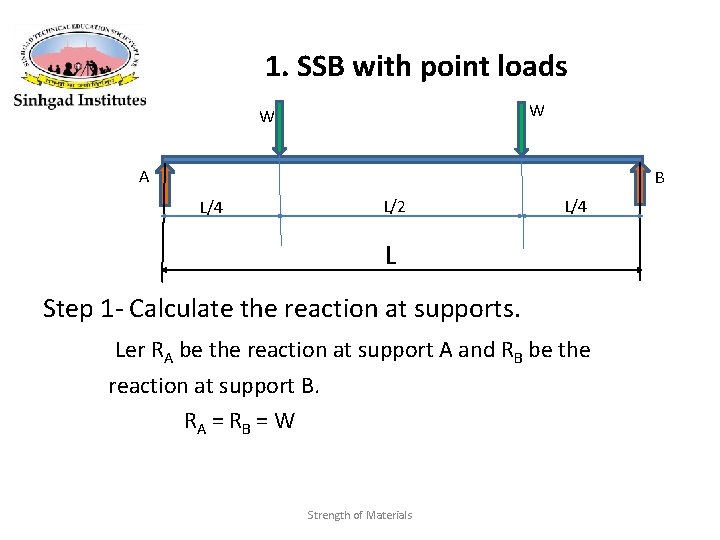
1. SSB with point loads W W A B L/4 L/2 L/4 L Step 1 - Calculate the reaction at supports. Ler RA be the reaction at support A and RB be the reaction at support B. R A = RB = W Strength of Materials

SSB with Point Loads Step 2 - Take a section X-X at a distance X from left end A W W A B L/2 L/4 L X Strength of Materials L/4

SSB with Point Loads Step 3 - Take moment of all forces about section x-x Step 4 – Separate the moment of each force by using compartment line Strength of Materials

SSB with Point Loads Step 5 – Use the differential deflection equation Step 6 – Equate the left hand side of it with step 5 equation Strength of Materials

SSB with Point Loads Step 7 - Integrate Step 8 - Again integrate Strength of Materials

SSB with Point Loads Step 9 - Apply BCs, at x=0, y=0, we get Put x=L, y=0 , we get Step 10 - Put Values of C 1 and C 2 in Step 7 and Step 8 to get Slope and Deflection equation Strength of Materials

SSB with Point Loads Slope Equation Deflection Equation Strength of Materials

SSB with Point Loads Slope at A, Put x=0 in slope eq. Slope at B, Put x=L Deflection at centre, put x=L/2, in deflection eq. Strength of Materials

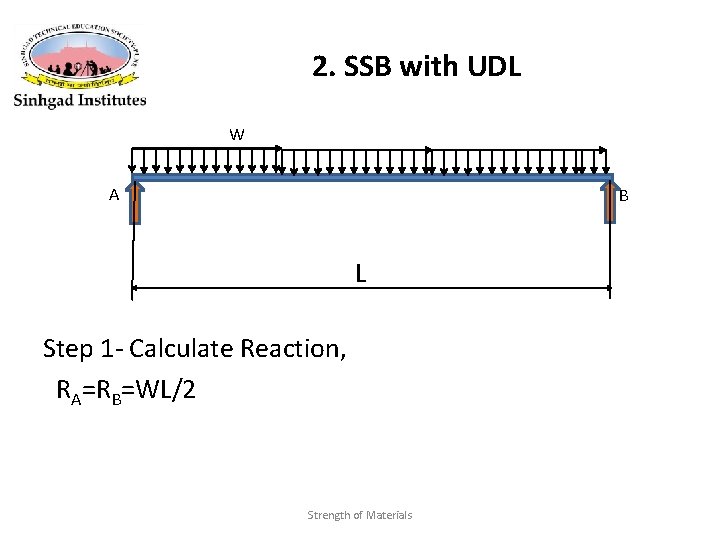
2. SSB with UDL W A B L Step 1 - Calculate Reaction, RA=RB=WL/2 Strength of Materials

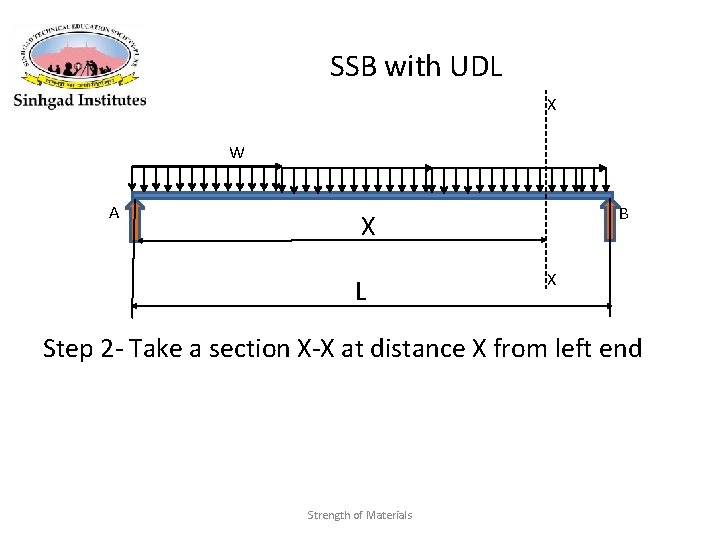
SSB with UDL X W A B X L X Step 2 - Take a section X-X at distance X from left end Strength of Materials

SSB with UDL Step 3 - Taking moment of all forces about Section X and equating it with Differential Deflection equation Step 4 - Integrate Strength of Materials

SSB with UDL Step 5 – Again Integrate Step 6 – Applying Boundary conditions, when x=0, y=0 in step 5, we get Put x=L, y=0, we get Strength of Materials

SSB with UDL Step 7 - put values of C 1 and C 2 in step 4 and 5 to get Slope and Deflection equation Slope Equation Deflection Equation Strength of Materials

SSB with UDL Slope at Support A, put x=0 in slope eq. , we get Slope at Support B, put x=L Maximum deflection, is about centre put x=L/2 in Deflection eq. , we get Strength of Materials

Numerical: 1 Strength of Materials

Workout Example : 1 • A simply supported beam of span L, carries a point load W at L/4 from each support. Find slope at support and maximum deflection. àDraw diagram àFollow Macaulays Method, as per previous derivations. àAns: Strength of Materials