standard basis beta basis standard basis beta basis

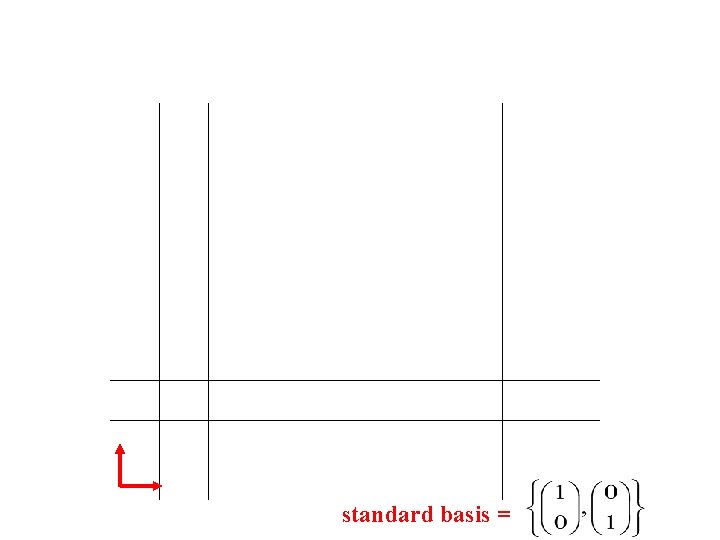
standard basis =

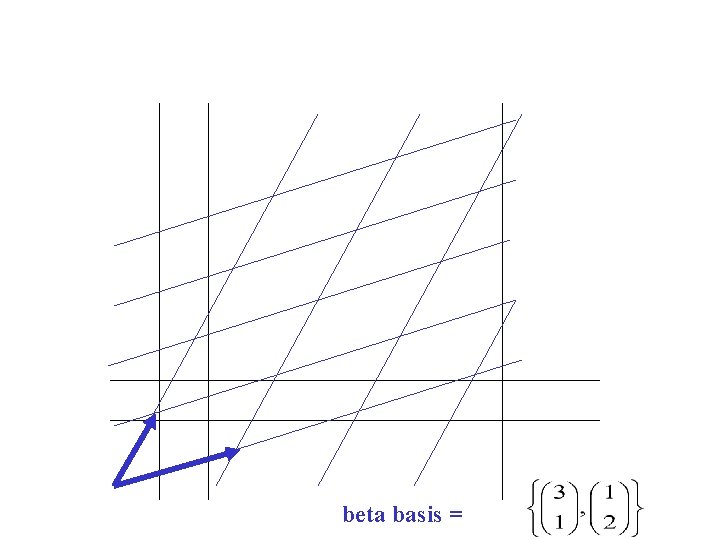
beta basis =

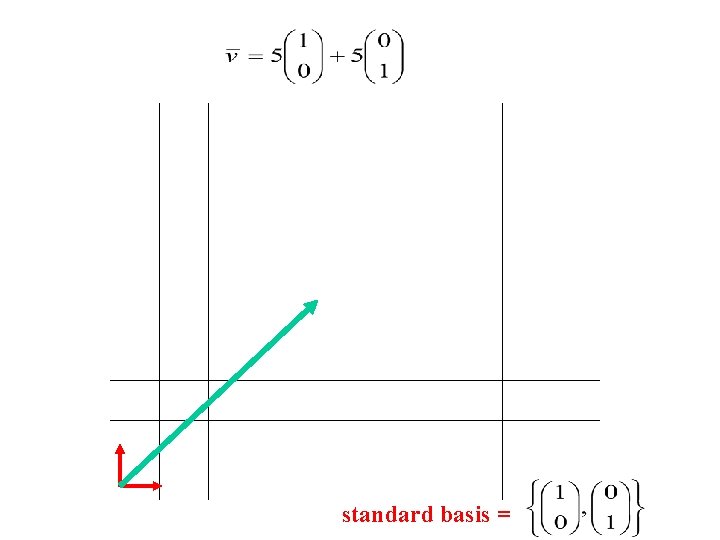
standard basis =

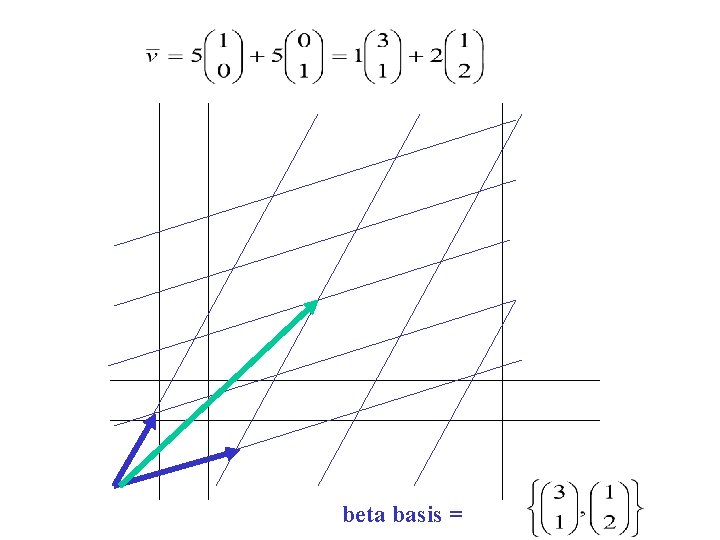
beta basis =

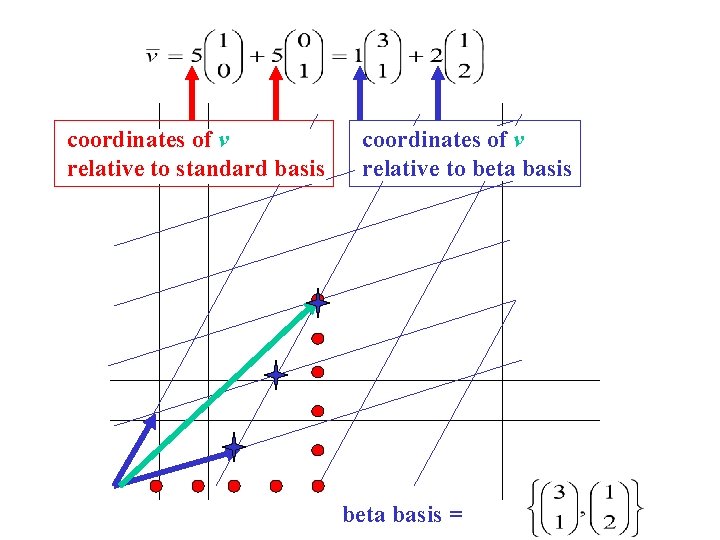
coordinates of v relative to standard basis coordinates of v relative to beta basis =

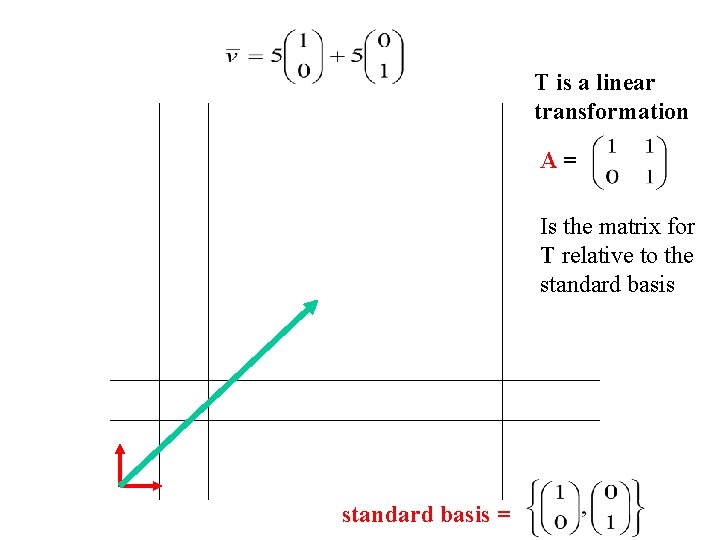
T is a linear transformation A= Is the matrix for T relative to the standard basis =

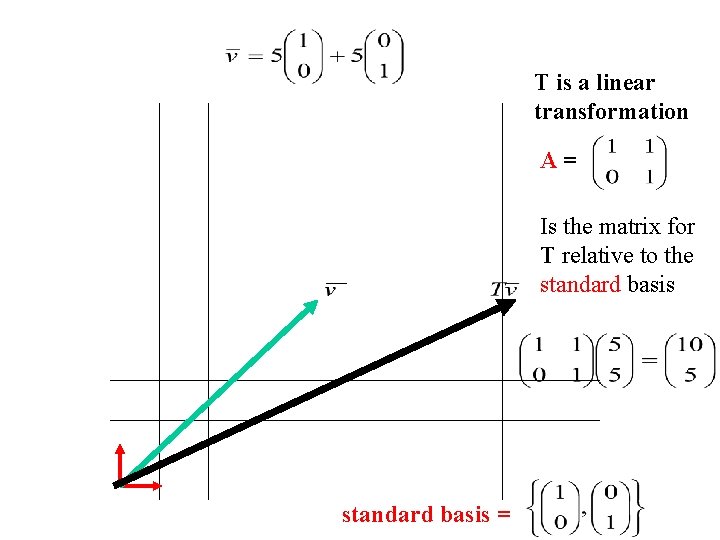
T is a linear transformation A= Is the matrix for T relative to the standard basis =

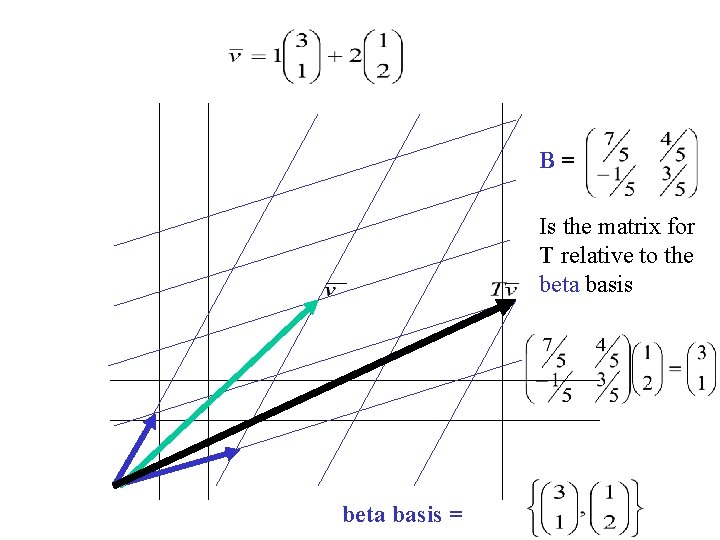
B= Is the matrix for T relative to the beta basis =

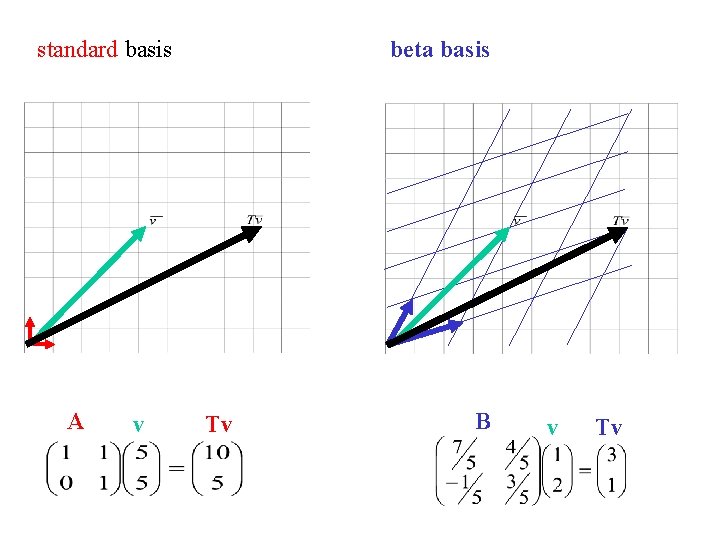
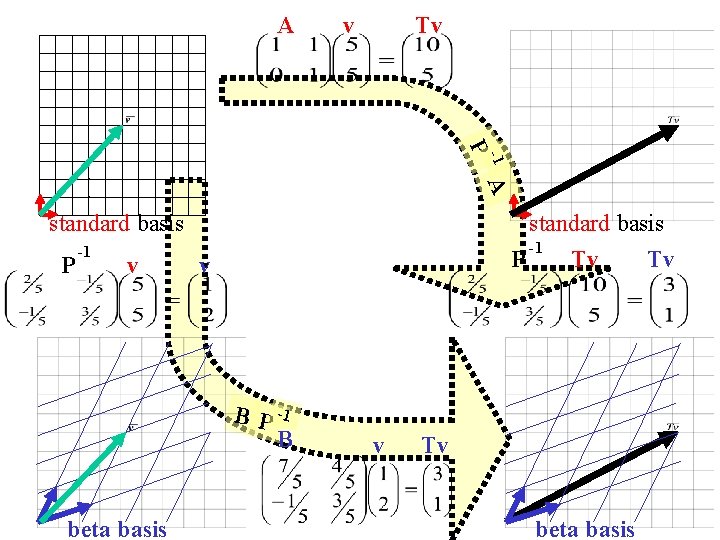
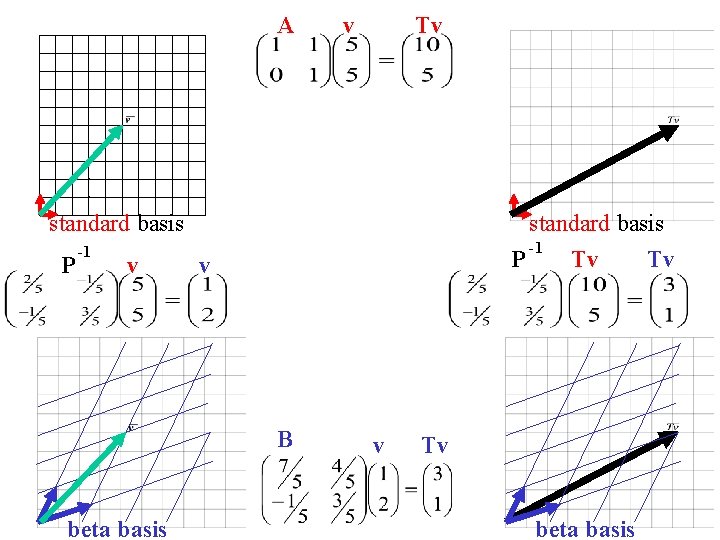
standard basis A v beta basis Tv B v Tv

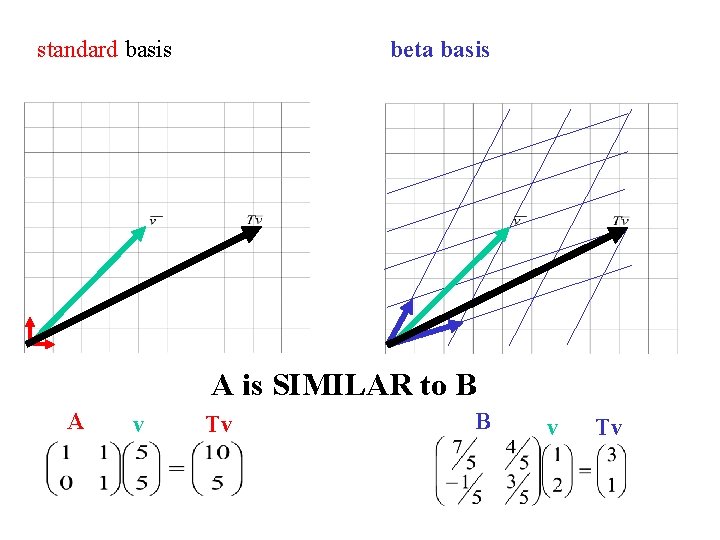
standard basis beta basis A is SIMILAR to B A v Tv B v Tv

beta basis =

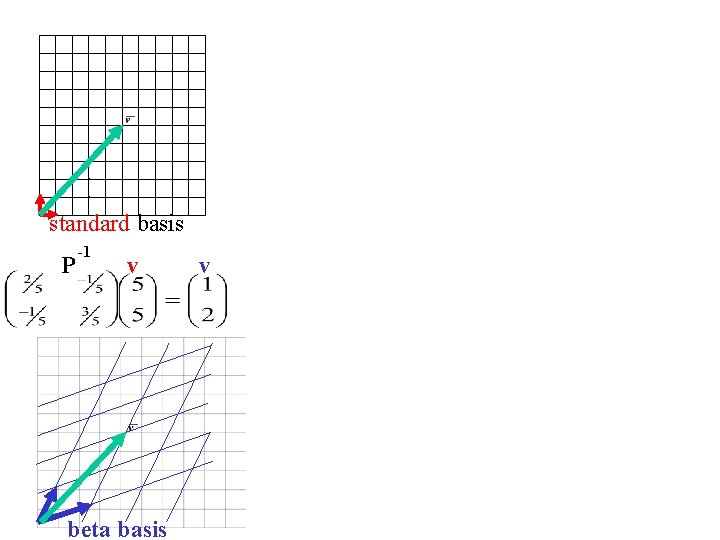
standard basis P -1 v beta basis v

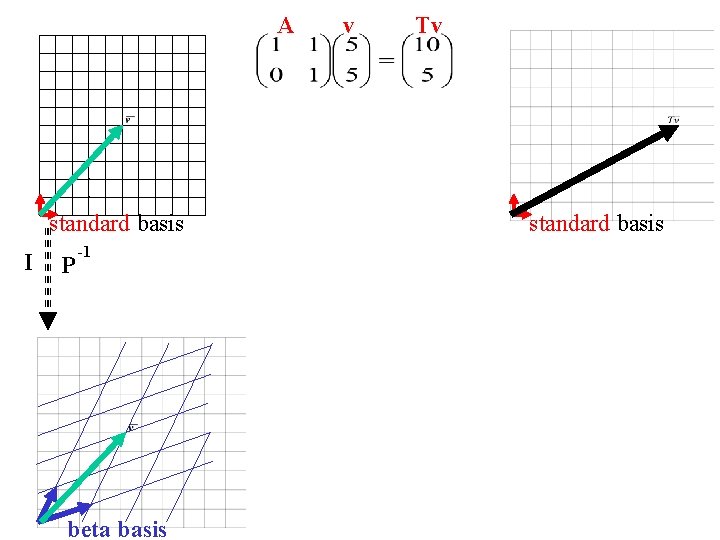
A standard basis I P -1 beta basis v Tv standard basis

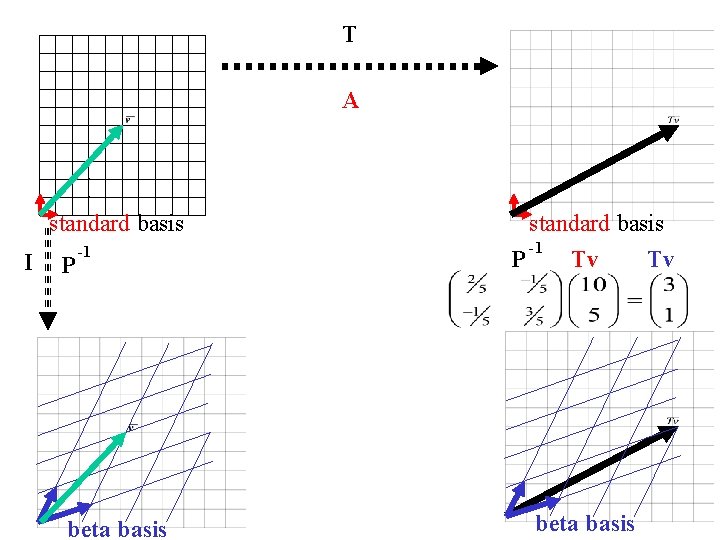
T A standard basis I P -1 beta basis standard basis -1 Tv Tv P beta basis

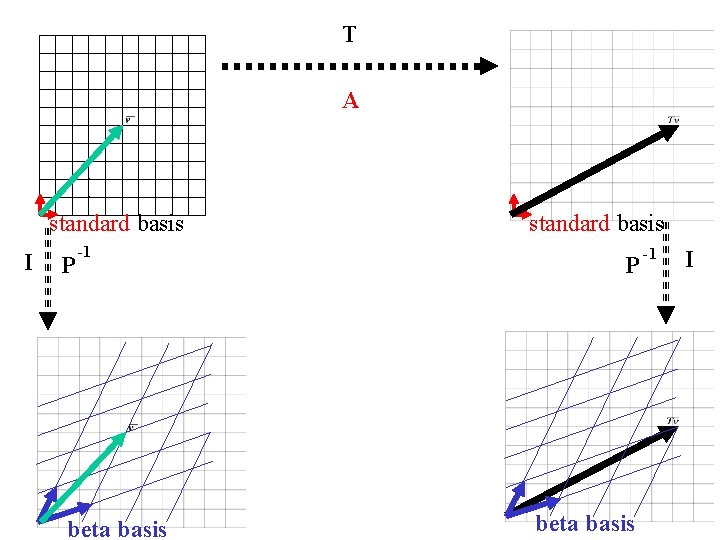
T A standard basis I P -1 beta basis standard basis P beta basis -1 I

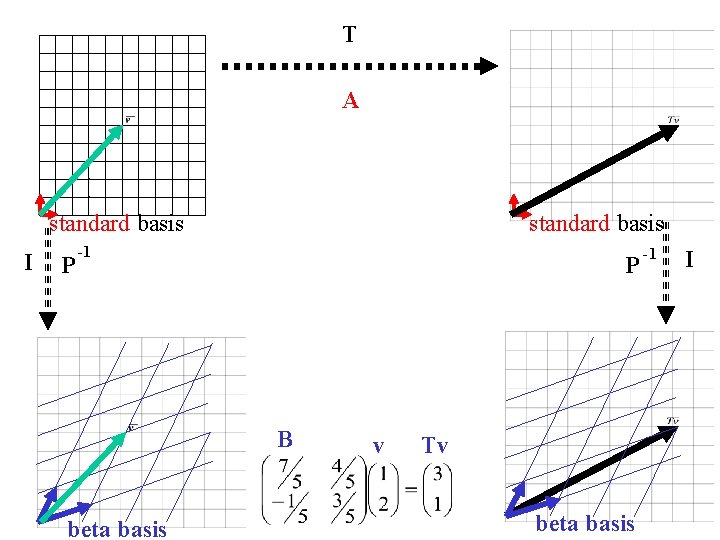
T A standard basis I P -1 P B beta basis v Tv beta basis -1 I

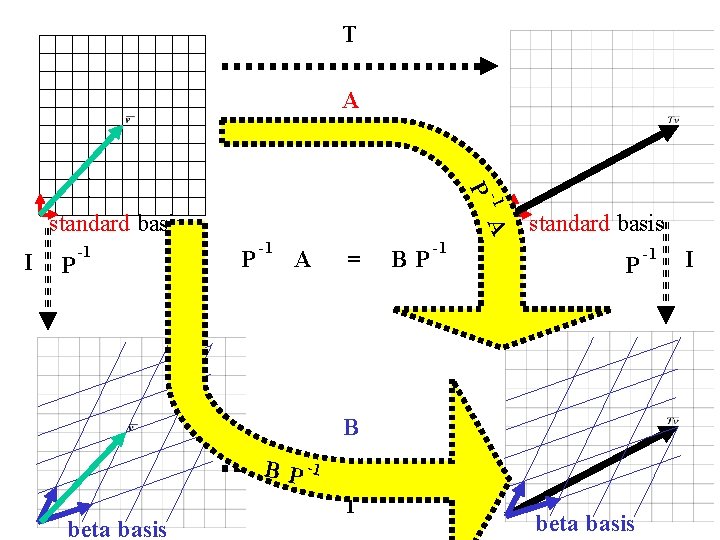
T A -1 P I P -1 A standard basis P -1 A = BP -1 standard basis P B B P -1 beta basis T beta basis -1 I

A v Tv -1 P A standard basis P -1 v P v B P -1 B beta basis v -1 Tv Tv beta basis Tv

A v Tv standard basis P -1 v standard basis -1 P Tv Tv v B beta basis v Tv beta basis

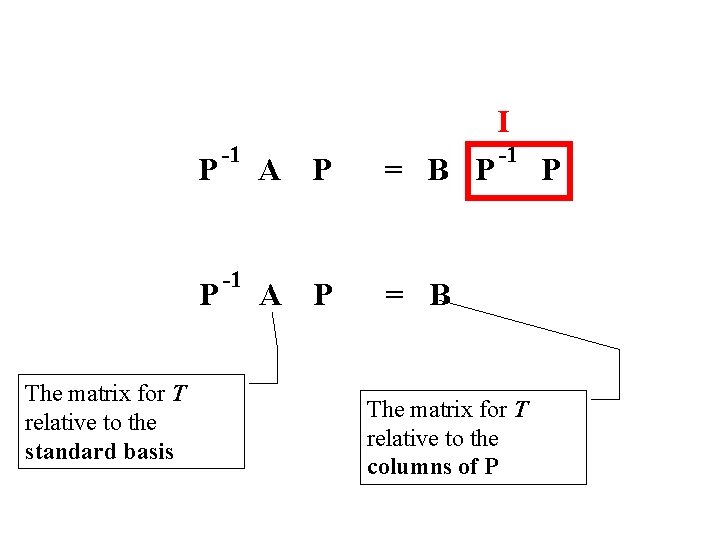
I The matrix for T relative to the standard basis P -1 A P = B P P -1 A P = B -1 The matrix for T relative to the columns of P P

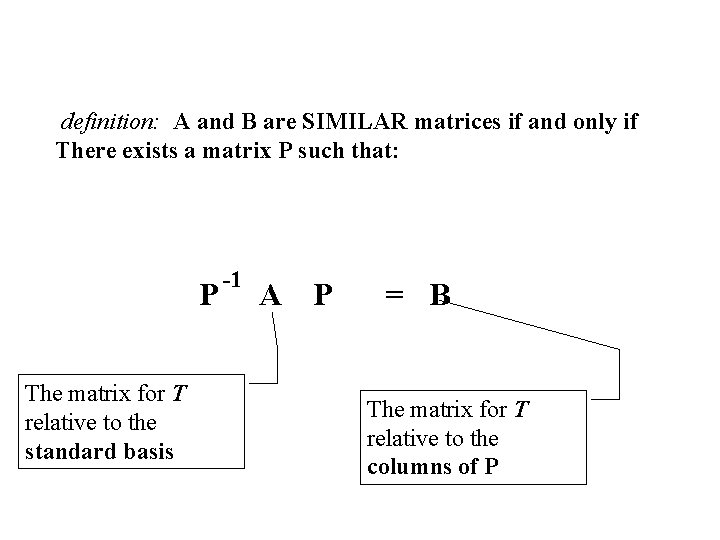
definition: A and B are SIMILAR matrices if and only if There exists a matrix P such that: P The matrix for T relative to the standard basis -1 A P = B The matrix for T relative to the columns of P