Stand Quietly Lesson 7 5 Distance Formula Students

Stand Quietly

Lesson 7. 5 Distance Formula Students will be able to use the distance formula to find the distance between two points. CCMS. 8. G. 6; CCMS. 8. G. 7; CCMS. 8. G. 8 2

Homework (10/20/2016) Worksheet: Distance Formula 3

Why do we use Pythagorean Theorem? To find the missing length, the distance between two locations

Distance Formula • Used to find the distance between two points

Example • Find the distance between A(4, 8) and B(1, 12) A (4, 8) B (1, 12)

Find the distance between: EXAMPLE 2: (2, 7) and (11, 9) EXAMPLE 3: (-5, 8) and (2, - 4)

Example 1: Using the Distance Formula Find FG and JK. Then determine whether FG JK. Step 1 Find the coordinates of each point. F(1, 2), G(5, 5), J(– 4, 0), K(– 1, – 3)

Example 1 Continued Step 2 Use the Distance Formula.

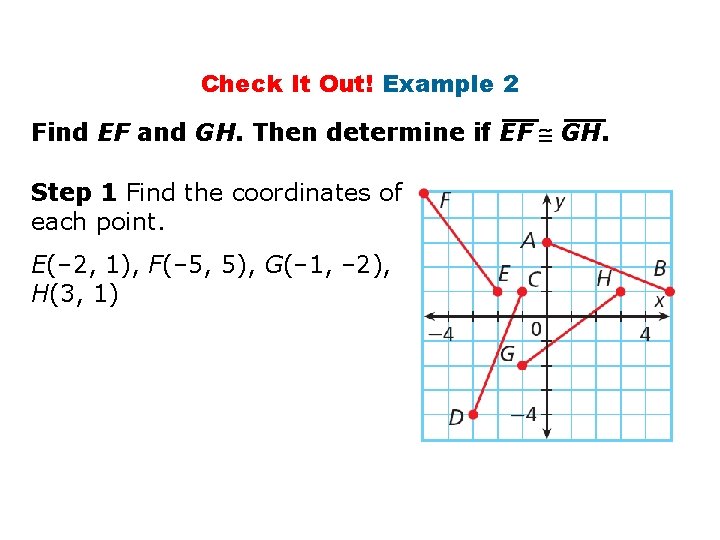
Check It Out! Example 2 Find EF and GH. Then determine if EF GH. Step 1 Find the coordinates of each point. E(– 2, 1), F(– 5, 5), G(– 1, – 2), H(3, 1)

Check It Out! Example 2 Continued Step 2 Use the Distance Formula.

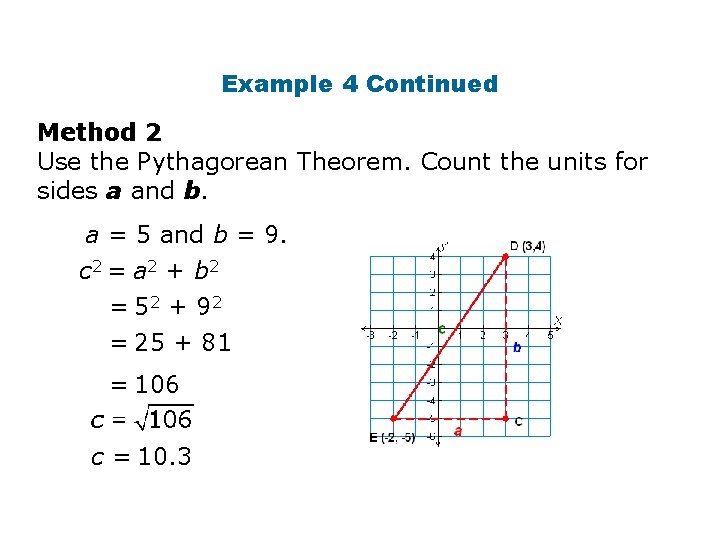
Example 3: Finding Distances in the Coordinate Plane Use the Distance Formula and the Pythagorean Theorem to find the distance, to the nearest tenth, from D(3, 4) to E(– 2, – 5).

Example 3 Continued Method 1 Use the Distance Formula. Substitute the values for the coordinates of D and E into the Distance Formula.

Example 4 Continued Method 2 Use the Pythagorean Theorem. Count the units for sides a and b. a = 5 and b = 9. c 2 = a 2 + b 2 = 52 + 9 2 = 25 + 81 = 106 c = 10. 3

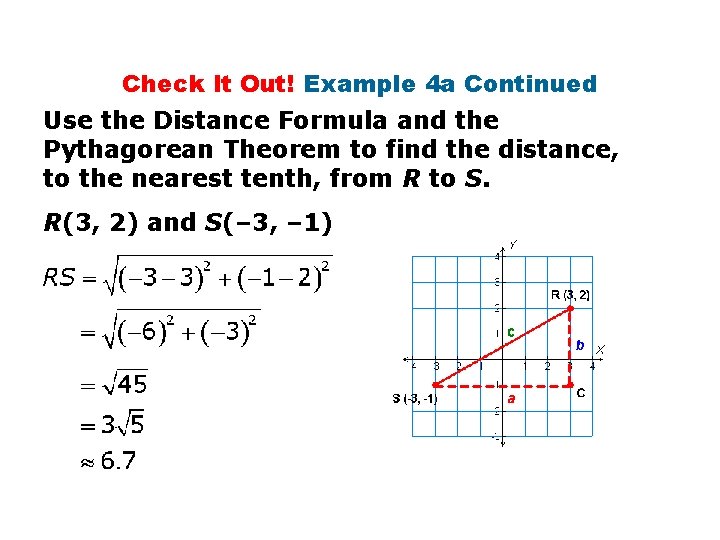
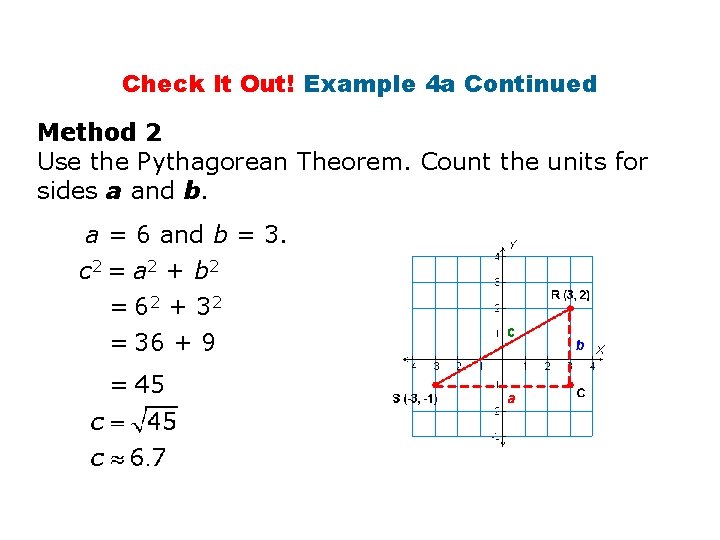
Check It Out! Example 4 a Continued Use the Distance Formula and the Pythagorean Theorem to find the distance, to the nearest tenth, from R to S. R(3, 2) and S(– 3, – 1)

Check It Out! Example 4 a Continued Method 2 Use the Pythagorean Theorem. Count the units for sides a and b. a = 6 and b = 3. c 2 = a 2 + b 2 = 62 + 3 2 = 36 + 9 = 45

Check It Out! Example 4 b Use the Distance Formula and the Pythagorean Theorem to find the distance, to the nearest tenth, from R to S. R(– 4, 5) and S(2, – 1) Method 1 Use the Distance Formula. Substitute the values for the coordinates of R and S into the Distance Formula.

Check It Out! Example 4 b Continued Use the Distance Formula and the Pythagorean Theorem to find the distance, to the nearest tenth, from R to S. R(– 4, 5) and S(2, – 1)

Check It Out! Example 4 b Continued Method 2 Use the Pythagorean Theorem. Count the units for sides a and b. a = 6 and b = 6. c 2 = a 2 + b 2 = 62 + 6 2 = 36 + 36 = 72

Lesson Quiz: Part I 1. Find the coordinates of the midpoint of MN with endpoints M(-2, 6) and N(8, 0). (3, 3) 2. K is the midpoint of HL. H has coordinates (1, – 7), and K has coordinates (9, 3). Find the coordinates of L. (17, 13) 3. Find the distance, to the nearest tenth, between S(6, 5) and T(– 3, – 4). 12. 7 4. The coordinates of the vertices of ∆ABC are A(2, 5), B(6, – 1), and C(– 4, – 2). Find the perimeter of ∆ABC, to the nearest tenth. 26. 5

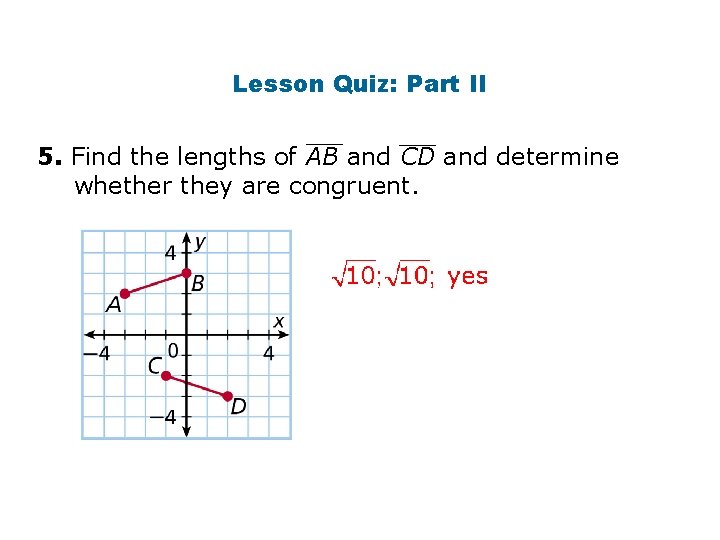
Lesson Quiz: Part II 5. Find the lengths of AB and CD and determine whether they are congruent.