Stand Quietly Lesson 6 1Relations and Functions Standard











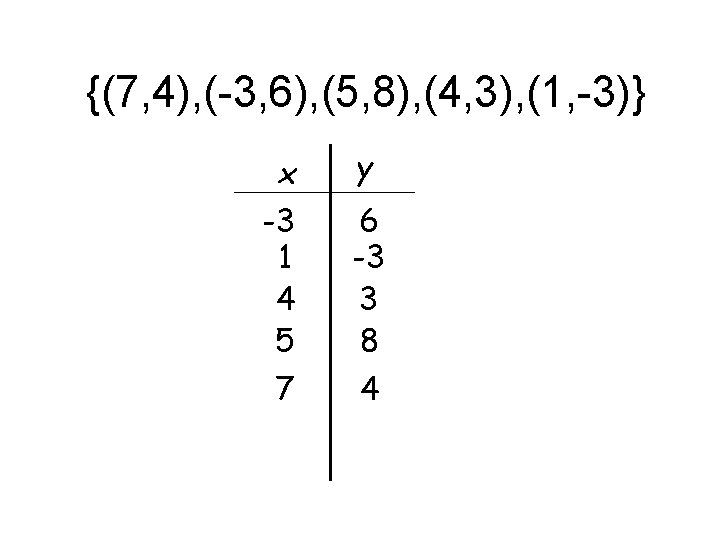




- Slides: 32

Stand Quietly

Lesson 6. 1_Relations and Functions Standard: CCSS. 8. F. 1. Students will be able to distinguish between relations that are functions and those that are not functions.

Warm-Up #17 (4/3/17) 1. Use substitution method to solve for x and y. y=4 x and 2 x+3 y=28 2. Is (1, -4) a solution to 2 x – y= 6 3. Name three forms of linear equations that you have learned.

Homework (4/3/17) Textbook Big Ideas page 246 #3 -12 ALL

relation is a set of _________. ordered pairs A ____ Relation = { (3, 5), (-2, 8), (-3, 8), (0, -6) } domain is the ______ set of ______ x The ____ values. range set y The ____ is the ______ of ______ values.

• An ordered pair consist of a x and ycoordinate • A relation may be viewed as ordered pairs, mapping design, table, graph, equation, or written in sentences • x-values are inputs, domain, independent variable • y-values are outputs, range, dependent variable 1/17/2022 1: 55 PM 1 -6 Relations and Functions 6

EXAMPLE Relation = { (3, 5), (-2, 8), (-3, 8), (0, -6) } Domain: { ____, ____} Range: {____ , ____}

EXAMPLE Relation = { (3, 5), (-2, 8), (-3, 8), (0, -6) } -3 ____, -2 ___, 0 ____} 3 Domain: { ____, Range: {____ , ____}

EXAMPLE Relation = { (3, 5), (-2, 8), (-3, 8), (0, -6) } -3 ____, -2 ___, 0 ____} 3 Domain: { ____, Range: {____} -6 , ___, 5 8

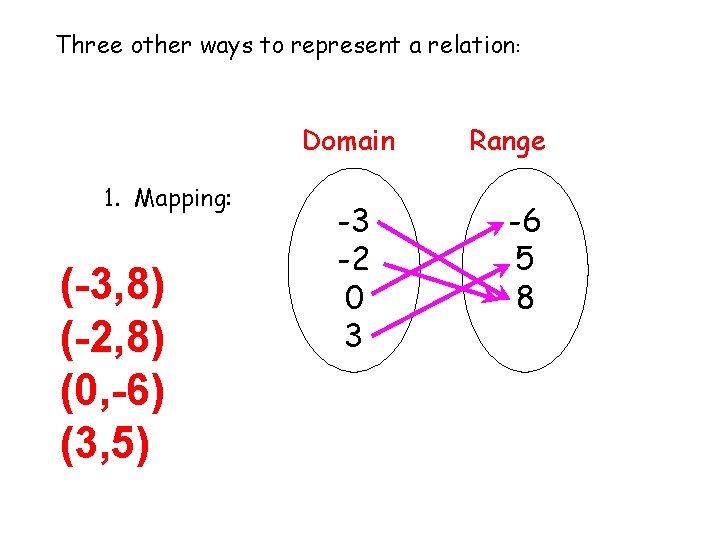
Three other ways to represent a relation: Domain 1. Mapping: (-3, 8) (-2, 8) (0, -6) (3, 5) -3 -2 0 3 Range -6 5 8

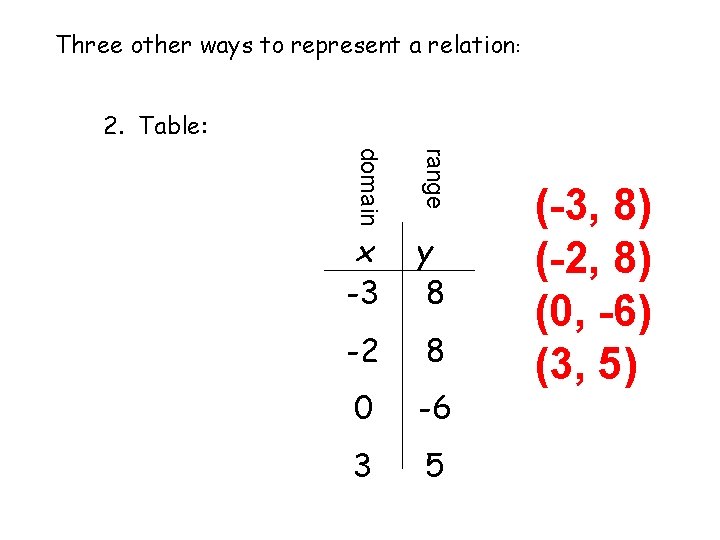
Three other ways to represent a relation: 2. Table: domain range x -3 y 8 -2 8 0 -6 3 5 (-3, 8) (-2, 8) (0, -6) (3, 5)

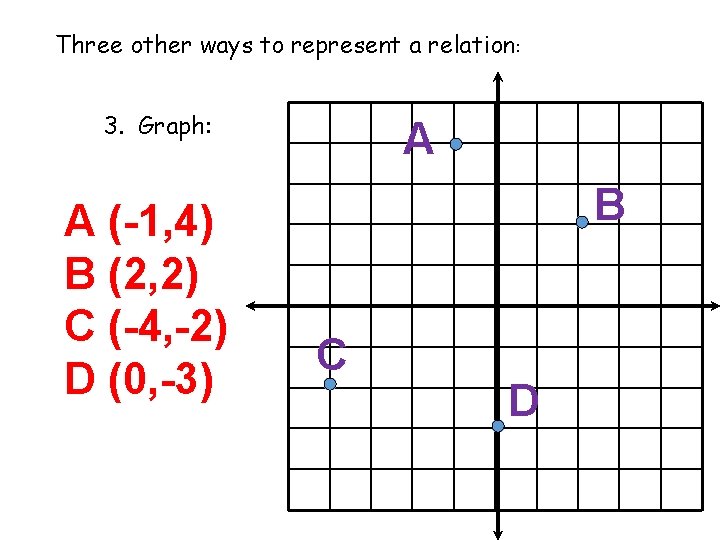
Three other ways to represent a relation: 3. Graph: A (-1, 4) B (2, 2) C (-4, -2) D (0, -3) A B C D

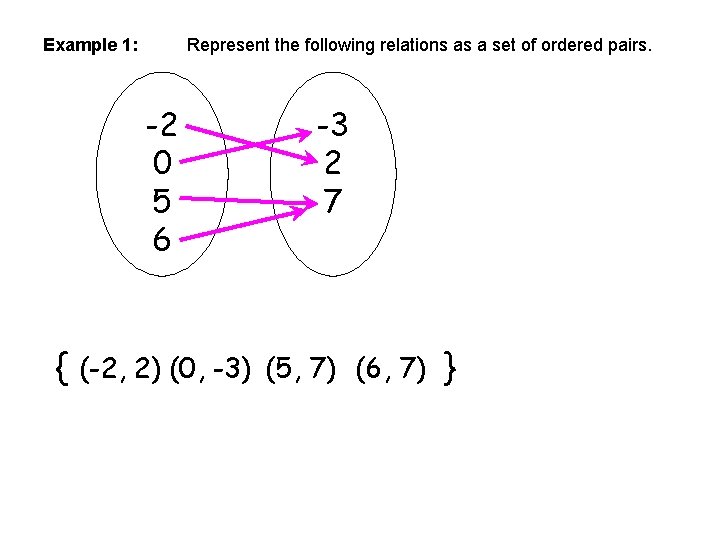
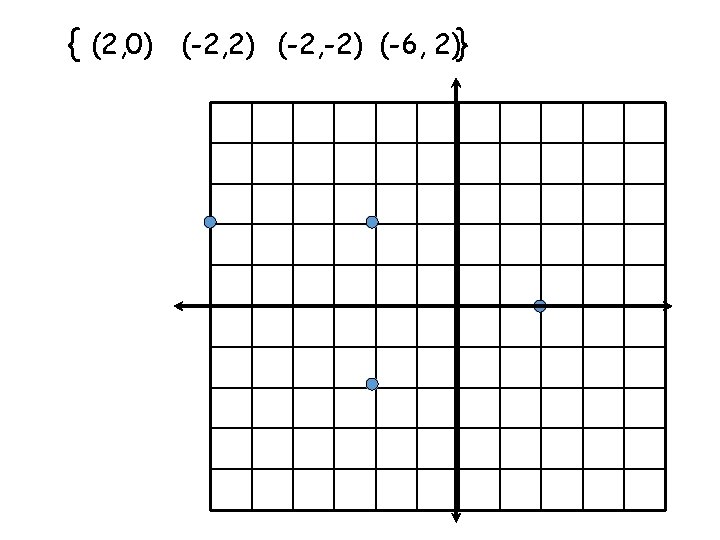
Example 1: Represent the following relations as a set of ordered pairs. -2 0 5 6 { -3 2 7 (-2, 2) (0, -3) (5, 7) (6, 7) }



Is a relation a function? • Focus on the x-coordinates, when given a relation. If the set of ordered pairs have different x-coordinates, it IS A function • If the set of ordered pairs have same x-coordinates, it is NOT a function • Y-coordinates have no affect of determining functions 1/17/2022 1: 55 PM 1 -6 Relations and Functions 16

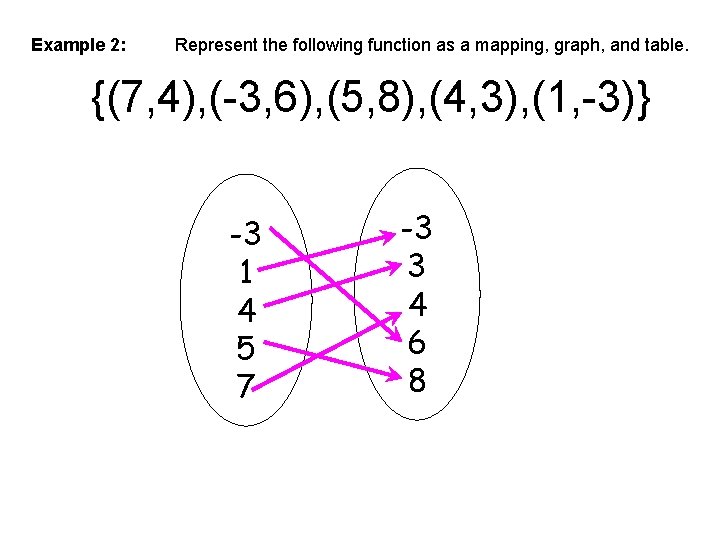
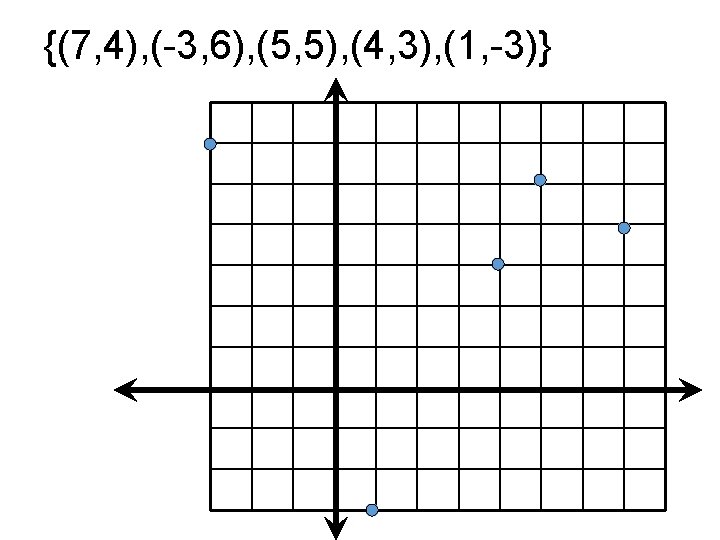
Example 2: Represent the following function as a mapping, graph, and table. {(7, 4), (-3, 6), (5, 8), (4, 3), (1, -3)} -3 1 4 5 7 -3 3 4 6 8

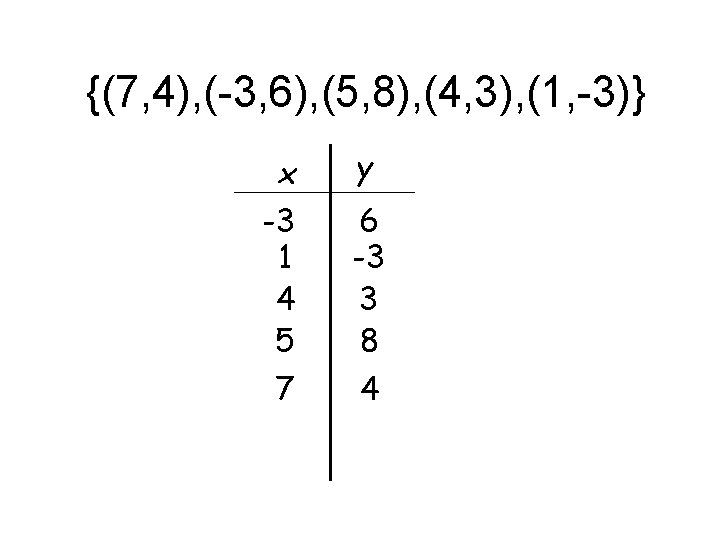
{(7, 4), (-3, 6), (5, 8), (4, 3), (1, -3)} x -3 1 4 5 7 y 6 -3 3 8 4

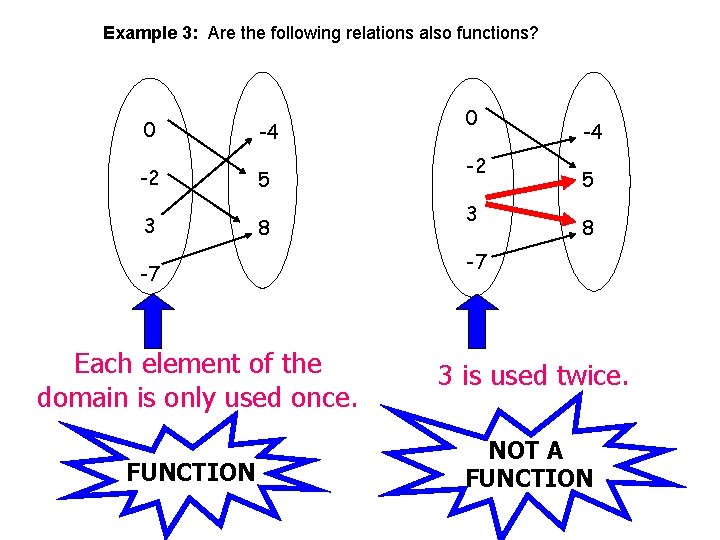
Example 3: Are the following relations also functions? 0 -4 -2 5 3 8 -7 0 -2 3 -4 5 8 -7 Each element of the domain is only used once. 3 is used twice. FUNCTION NOT A FUNCTION

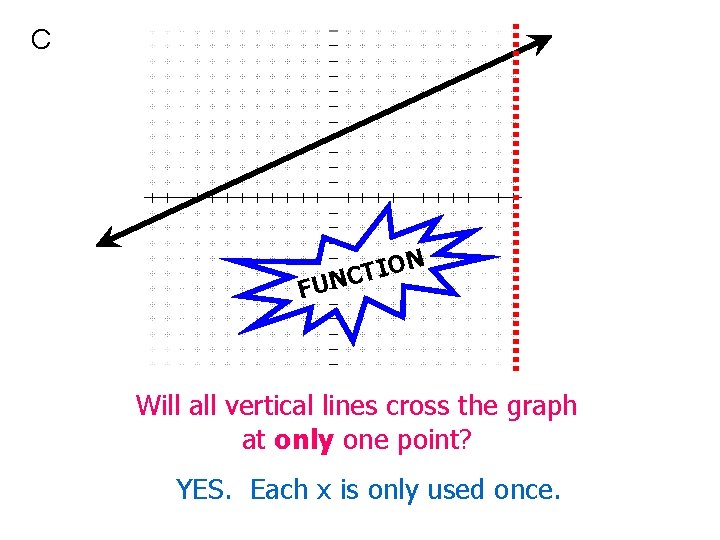
C N O I T NC FU Will all vertical lines cross the graph at only one point? YES. Each x is only used once.

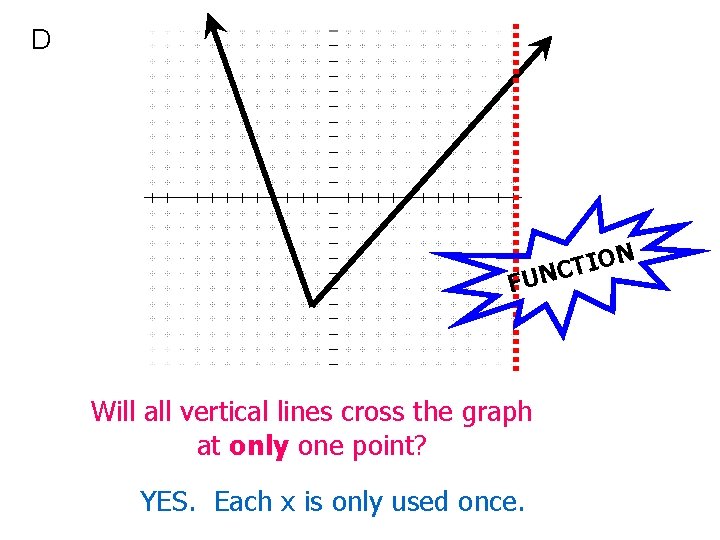
D N IO T C UN F Will all vertical lines cross the graph at only one point? YES. Each x is only used once.

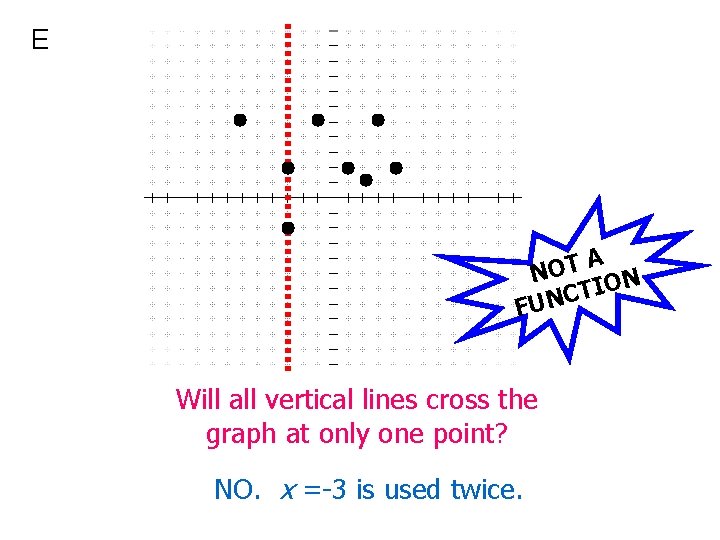
E A NOT ON TI C N FU Will all vertical lines cross the graph at only one point? NO. x =-3 is used twice.

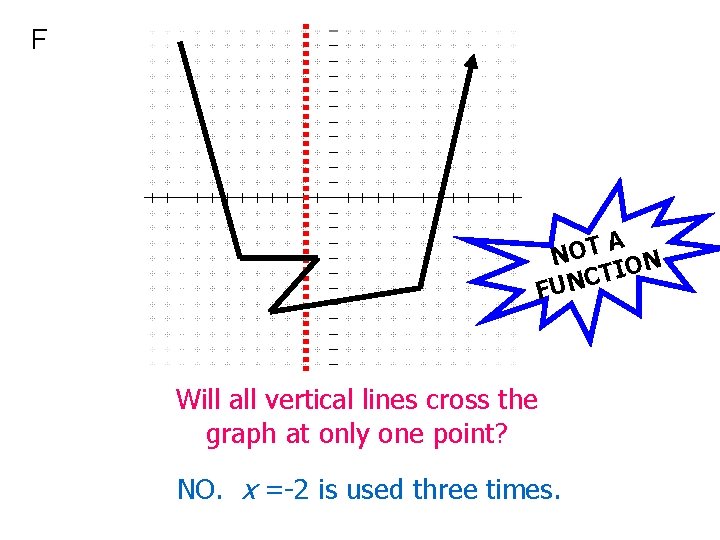
F A T O N N O I T C FUN Will all vertical lines cross the graph at only one point? NO. x =-2 is used three times.

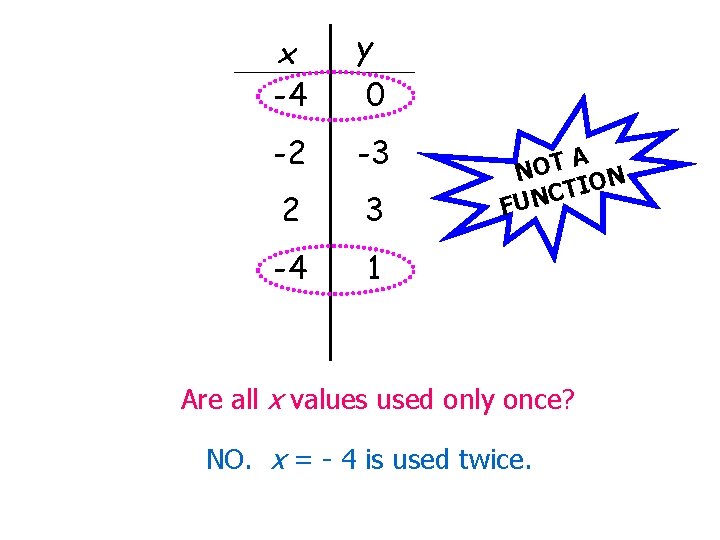
x -4 y 0 -2 -3 2 3 -4 1 A T O N N O I T C FUN Are all x values used only once? NO. x = - 4 is used twice.

Example 1 • What is the domain? {0, 1, 2, 3, 4, 5} What is the range? {-5, -4, -3, -2, -1, 0} 1/17/2022 1: 55 PM 1 -6 Relations and Functions 26

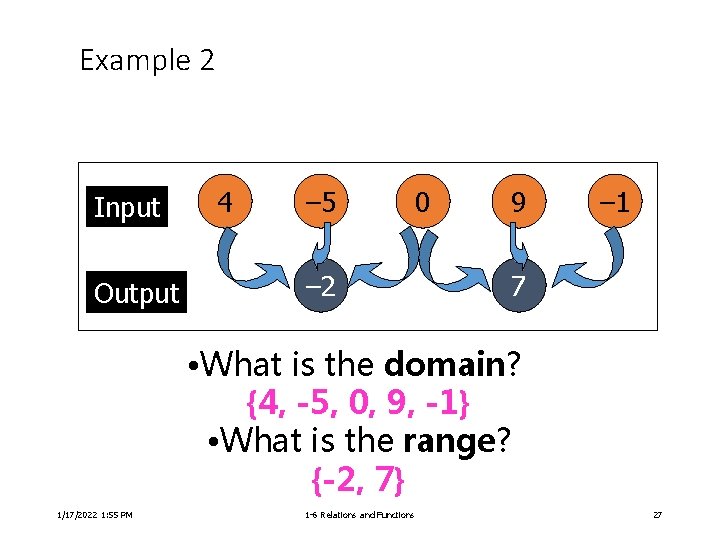
Example 2 Input Output 4 – 5 – 2 0 9 – 1 7 • What is the domain? {4, -5, 0, 9, -1} • What is the range? {-2, 7} 1/17/2022 1: 55 PM 1 -6 Relations and Functions 27

Example 3 • Is this a function? • Hint: Look only at the x-coordinates YES 1/17/2022 1: 55 PM 1 -6 Relations and Functions 28

Example 4 • Is this a function? • Hint: Look only at the x-coordinates NO 1/17/2022 1: 55 PM 1 -6 Relations and Functions 29

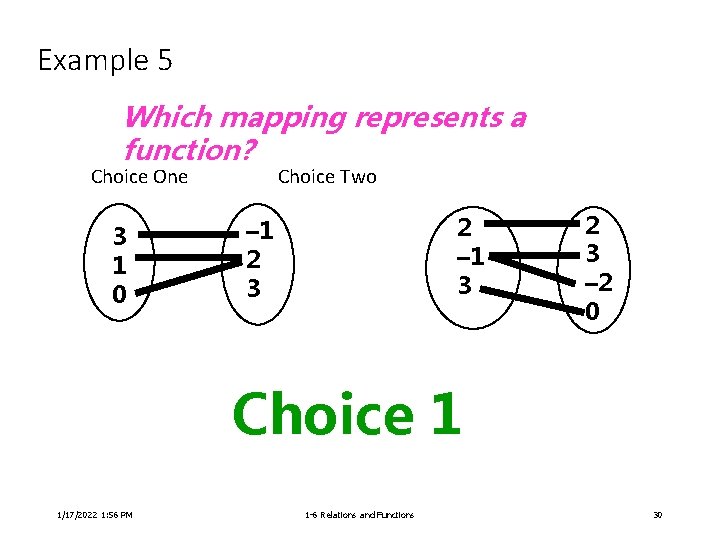
Example 5 Which mapping represents a function? Choice One 3 1 0 Choice Two 2 – 1 3 – 1 2 3 – 2 0 Choice 1 1/17/2022 1: 56 PM 1 -6 Relations and Functions 30

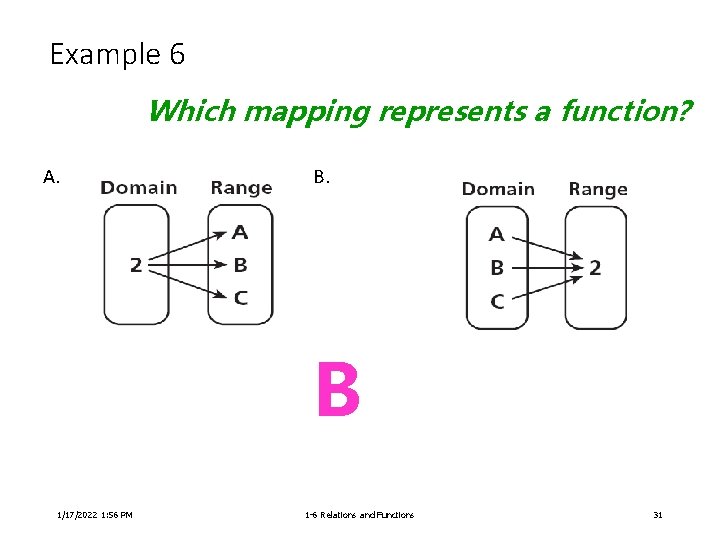
Example 6 Which mapping represents a function? A. B 1/17/2022 1: 56 PM 1 -6 Relations and Functions 31

Example 7 Which situation represents a function? a. The items in a store to their prices on a certain date b. Types of fruits to their colors There is only one price for each different item on a certain date. The relation from items to price makes it a function. 1/17/2022 1: 56 PM A fruit, such as an apple, from the domain would be associated with more than one color, such as red and green. The relation from types of fruits to their colors is not a function. 1 -6 Relations and Functions 32