Stand Quietly Lesson 5 6 Direct Variation Student

Stand Quietly

Lesson 5. 6 Direct Variation Student will be able to write and graph an equation of a direct variation.

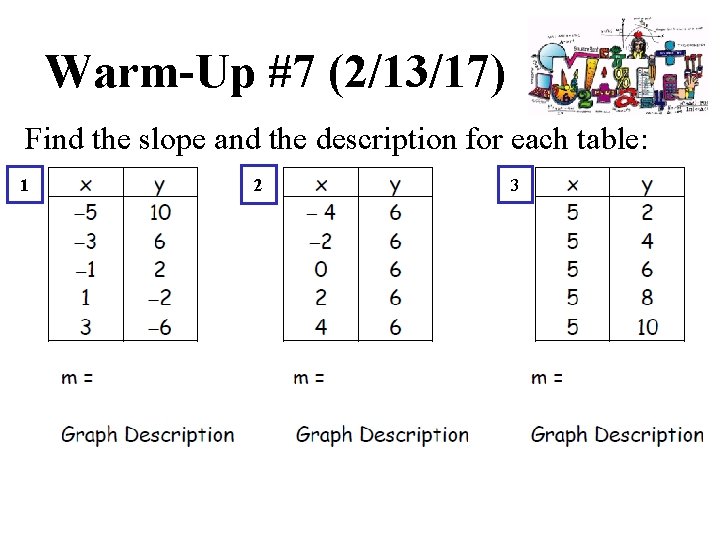
Warm-Up #7 (2/13/17) Find the slope and the description for each table: 1 2 3

Homework (2/13/17) Lesson 5. 5 Packet_ Finish

Warm-Up #8 (2/15/17) •

Homework (2/15/17) Worksheet: Proportional Relationships Classnotes

Definition •

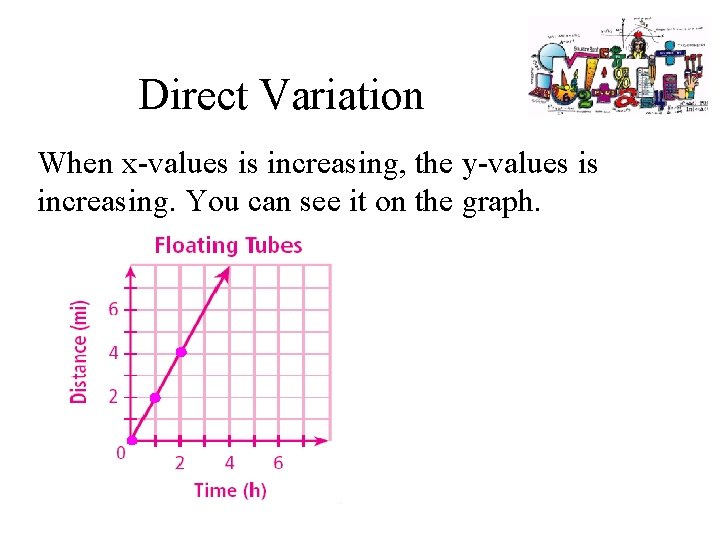
Direct Variation When x-values is increasing, the y-values is increasing. You can see it on the graph.

Direct Variation A recipe for paella calls for 1 cup of rice to make 5 servings. In other words, a chef needs 1 cup of rice for every 5 servings. The equation y = 5 x describes this relationship. In this relationship, the number of servings varies directly with the number of cups of rice.

Determining Direct Variation • To determine whether an equation represents a direct variation: 1) Given an equation. Ø Solve for y. Ø If you can write the equation in the form y = mx, where m ≠ 0, then it is a direct variation.

Determining Direct Variation 2) Given a table of values. Ø Find y/x for each ordered pair. Ø If the ratio y/x is constant for all ordered pairs, then it is a direct variation. 3) Given a graph. Ø The graph is a line and passes through the origin, then it is a direct variation. Ø The slope of the line is m.

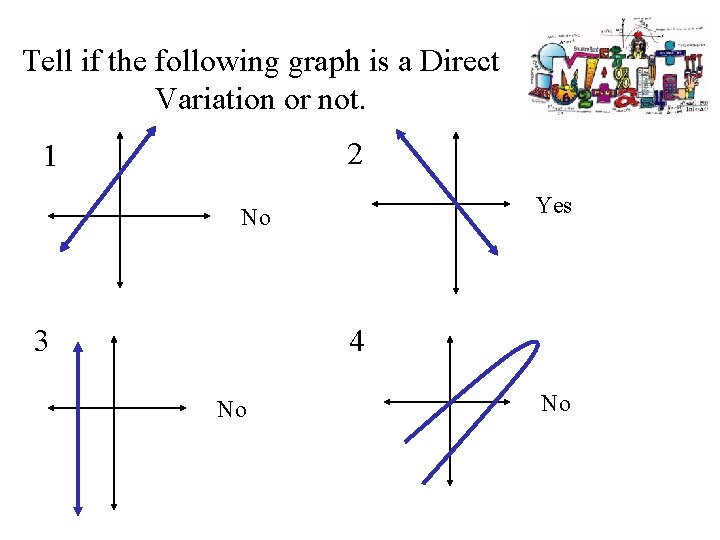
Tell if the following graph is a Direct Variation or not. 2 1 Yes No 3 4 No No

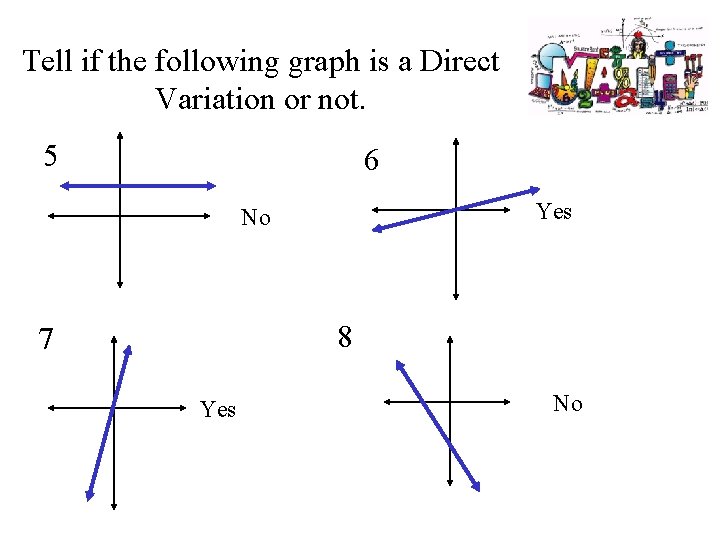
Tell if the following graph is a Direct Variation or not. 5 6 Yes No 8 7 Yes No

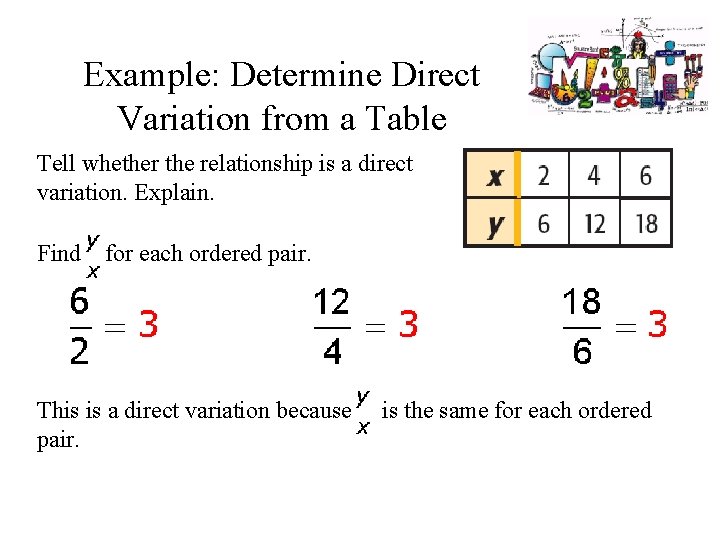
Example: Determine Direct Variation from a Table Tell whether the relationship is a direct variation. Explain. Find for each ordered pair. This is a direct variation because pair. is the same for each ordered

Example: Determine Direct Variation from a Table Tell whether the relationship is a direct variation. Explain. Find for each ordered pair. … This is not direct variation because ordered pairs. is the not the same for all

Your Turn: Tell whether the relationship is a direct variation. Explain. Find for each ordered pair. This is not direct variation because ordered pairs. is the not the same for all

Your Turn: Tell whether the relationship is a direct variation. Explain. Find for each ordered pair. This is a direct variation because pair. is the same for each ordered

Your Turn: Tell whether the relationship is a direct variation. Explain. Find for each ordered pair. This is not direct variation because ordered pairs. is the not the same for all

Example: Determine Direct Variation from an Equation Tell whether the equation represents a direct variation. If so, identify the constant of variation. Example : y = 3 x This equation represents a direct variation because it is in the form of y = kx. The constant of variation is 3.

Example: Determine Direct Variation from an Equation Tell whether the equation represents a direct variation. If so, identify the constant of variation. 3 x + y = 8 – 3 x y = – 3 x + 8 Solve the equation for y. Since 3 x is added to y, subtract 3 x from both sides. This equation is not a direct variation because it cannot be written in the form y = kx.

Example: Determine Direct Variation from an Equation Tell whether the equation represents a direct variation. If so, identify the constant of variation. – 4 x + 3 y = 0 +4 x 3 y = 4 x Solve the equation for y. Since – 4 x is added to 3 y, add 4 x to both sides. Since y is multiplied by 3, divide both sides by 3. This equation represents a direct variation because it is in the form of y = kx. The constant of variation is.

Your Turn: Tell whether the equation represents a direct variation. If so, identify the constant of variation. 3 y = 4 x + 1 This equation is not a direct variation because it is not written in the form y = kx.

Your Turn: Tell whether the equation represents a direct variation. If so, identify the constant of variation. Solve the equation for y. 3 x = – 4 y = 3 x Since y is multiplied by – 4, divide both sides by – 4. This equation represents a direct variation because it is in the form of y = kx. The constant of variation is.

Your Turn: Tell whether the equation represents a direct variation. If so, identify the constant of variation. y + 3 x = 0 – 3 x y = – 3 x Solve the equation for y. Since 3 x is added to y, subtract 3 x from both sides. This equation represents a direct variation because it is in the form of y = kx. The constant of variation is – 3.

Determine Direct Variation from a Table What happens if you solve y = kx for k? y = kx Divide both sides by x (x ≠ 0). So, in a direct variation, the ratio is equal to the constant of variation. Another way to identify a direct variation is to check whether is the same for each ordered pair (except where x = 0).

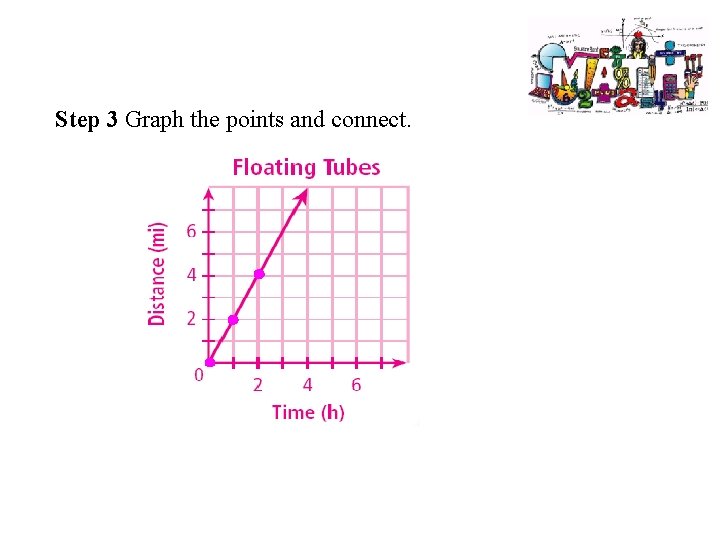
Example: Graphing Direct Variation A group of people are tubing down a river at an average speed of 2 mi/h. Write a direct variation equation that gives the number of miles y that the people will float in x hours. Then graph. Step 1 Write a direct variation equation. distance y = = 2 mi/h 2 times hours x

Example: Continued Step 2 Choose values of x and generate ordered pairs. x y = 2 x (x, y) 0 y = 2(0) = 0 (0, 0) 1 y = 2(1) = 2 (1, 2) 2 y = 2(2) = 4 (2, 4)

Step 3 Graph the points and connect.

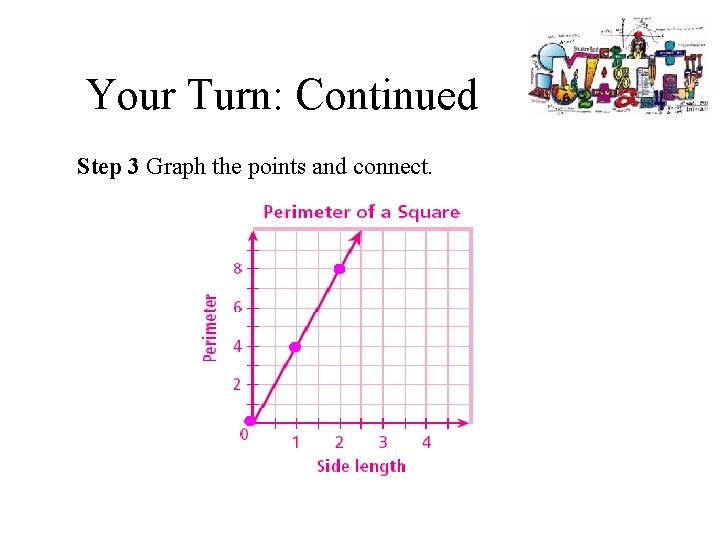
Your Turn: The perimeter y of a square varies directly with its side length x. Write a direct variation equation for this relationship. Then graph. Step 1 Write a direct variation equation. perimeter = y = 4 sides 4 times • length x

Your Turn: Continued Step 2 Choose values of x and generate ordered pairs. x y = 4 x (x, y) 0 y = 4(0) = 0 (0, 0) 1 y = 4(1) = 4 (1, 4) 2 y = 4(2) = 8 (2, 8)

Your Turn: Continued Step 3 Graph the points and connect.