STACS 2006 Amortized Rigidness in Dynamic Cartesian Trees

STACS 2006 Amortized Rigidness in Dynamic Cartesian Trees Iwona Białynicka-Birula and Roberto Grossi Università di Pisa 23 February 2006 23 rd International Symposium on Theoretical Aspects of Computer

Cartesian trees Vuillemin 1980 n Nodes store points 〈x, y〉 n n n y value can be viewed as priority Recursive definition Root stores point with greatest y value n x value partitions remaining points (left and right subtrees) n 23 February 2006 23 rd International Symposium on Theoretical Aspects of Computer Science 2

Cartesian tree example 〈 2, 22〉 〈 19, 21〉 〈 21, 20〉 〈 18, 19〉 〈 4, 18〉 〈 6, 17〉 〈 20, 16〉 〈 7, 15〉 〈 8, 13〉 〈 5, 12〉 〈 9, 11〉 〈 3, 9〉 〈 10, 7〉 〈 1, 2〉 23 February 2006 〈 17, 10〉 〈 16, 8〉 〈 14, 5〉 〈 15, 4〉 〈 12, 3〉 〈 22, 6〉 〈 11, 1〉 23 rd International Symposium on Theoretical Aspects of Computer Science 3

Applications Priority queue n Randomized searching (treaps) n Range and dominance searching n RMQ (Range Maximum Query) n LCA (Least Common Ancestor) n Integer sorting n Memory management n Suffix trees n. . . n 23 February 2006 23 rd International Symposium on Theoretical Aspects of Computer Science 4

From RMQ to LCA 22 21 19 18 17 16 15 12 13 11 10 9 8 7 5 2 20 3 6 4 1 2, 22, 9, 18, 12, 17, 15, 13, 11, 7, 1, 1 3, 5, 4, 8, 10, 19, 21, 16, 20, 6 23 February 2006 23 rd International Symposium on Theoretical Aspects of Computer Science 5

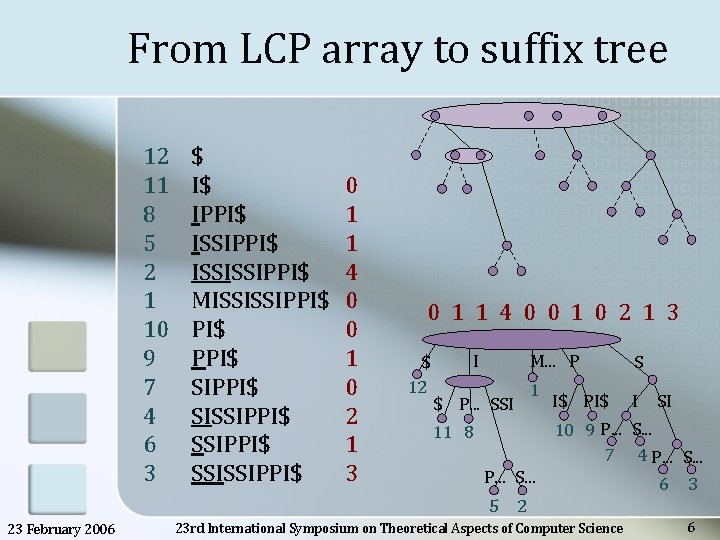
From LCP array to suffix tree 12 11 8 5 2 1 10 9 7 4 6 3 $ I$ IPPI$ ISSISSIPPI$ MISSISSIPPI$ SISSIPPI$ SSISSIPPI$ 0 1 1 4 0 0 1 0 2 1 3 $ 12 I M. . . P $ P. . . SSI 11 8 P. . . S. . . 5 23 February 2006 1 I$ PI$ S I SI 10 9 P. . . S. . . 7 4 P. . . S. . . 6 3 2 23 rd International Symposium on Theoretical Aspects of Computer Science 6

History n Static setting n n O(n) construction time, provided elements already sorted Randomized n Random priority values – treaps n O(log n) expected height n O(log n) expected update time n n Dynamic and deterministic n 23 February 2006 Other distributions yield O(√n) or even O(n) height (Devroye 1994) ? ? ? 23 rd International Symposium on Theoretical Aspects of Computer Science 7

Our result n Dynamic Cartesian tree Supports insertion n Supports weak deletion n Maintains actual tree structure between each operation n O(log n) amortized time per operation n 23 February 2006 23 rd International Symposium on Theoretical Aspects of Computer Science 8

Solution outline n Combinatorial analysis How many tree elements change due to n insertions? n Notion of entropy is exploited n n Auxiliary structure for accessing tree Needed to quickly access tree elements which need to change n Based on the interval tree n 23 February 2006 23 rd International Symposium on Theoretical Aspects of Computer Science 9

Insertion 〈 2, 22〉 〈 19, 21〉 〈 21, 20〉 〈 18, 19〉 〈 4, 18〉 〈 6, 17〉 〈 20, 16〉 〈 7, 15〉 〈 8, 13〉 〈 5, 12〉 〈 9, 11〉 〈 13, 14〉 〈 3, 9〉 〈 10, 7〉 〈 1, 2〉 23 February 2006 〈 17, 10〉 〈 16, 8〉 〈 14, 5〉 〈 15, 4〉 〈 12, 3〉 〈 22, 6〉 〈 11, 1〉 23 rd International Symposium on Theoretical Aspects of Computer Science 10

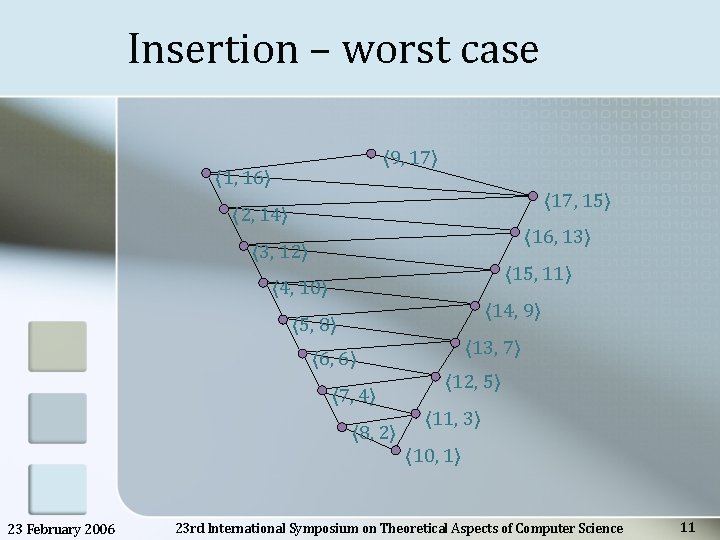
Insertion – worst case 〈 9, 17〉 〈 1, 16〉 〈 17, 15〉 〈 2, 14〉 〈 16, 13〉 〈 3, 12〉 〈 15, 11〉 〈 4, 10〉 〈 14, 9〉 〈 5, 8〉 〈 6, 6〉 〈 7, 4〉 〈 8, 2〉 23 February 2006 〈 13, 7〉 〈 12, 5〉 〈 11, 3〉 〈 10, 1〉 23 rd International Symposium on Theoretical Aspects of Computer Science 11

Analysis – main idea Inserting new elements does not require comparing y coordinates of existing points n In turn, deleting points does n Conclusion: insertions reduce tree information content n. . . so information entropy can be used as a potential function in an amortized analysis n 23 February 2006 23 rd International Symposium on Theoretical Aspects of Computer Science 12

Insertion revisited > > > > > 23 February 2006 > > 23 rd International Symposium on Theoretical Aspects of Computer Science 13

Insertion reversed (deletion) ? ? ? 23 February 2006 23 rd International Symposium on Theoretical Aspects of Computer Science 14

Formally. . . n Tree T induces partial order ≺T on nodes n 23 February 2006 Information needed to sort nodes given tree topology J G > We define missing entropy: ℋ(T)=log ℒ(T) I > > n Linear extensions are permutations satisfying the order, i. e. P[i] ≺T P[j] ⇒ i < j D > n A E > > Partial order ≺T has ℒ(T) linear extensions > > n Defined by the heap condition B > n C F H ABHJFGIDEC HAJFGIDBEC AJDFHGIBEC DJIAHFGEBC HJDAFGIEBC ADHFGJIBEC. . . 23 rd International Symposium on Theoretical Aspects of Computer Science 15

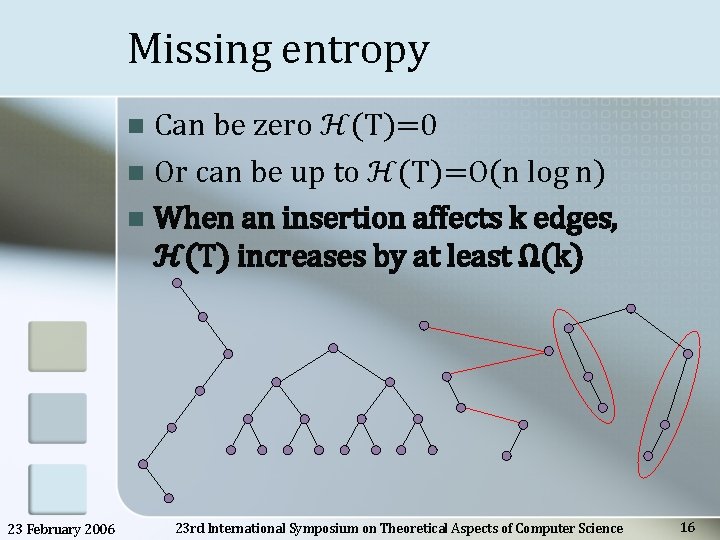
Missing entropy Can be zero ℋ(T)=0 n Or can be up to ℋ(T)=O(n log n) n When an insertion affects k edges, ℋ(T) increases by at least Ω(k) n 23 February 2006 23 rd International Symposium on Theoretical Aspects of Computer Science 16

So what now? n Amortized number of edge modifications is O(log n) per insertion into an initially empty tree n n But how to access the edges to modify? n 23 February 2006 Node modifications are always constant Without increasing the complexity 23 rd International Symposium on Theoretical Aspects of Computer Science 17

Implementation overview Companion interval tree stores tree edges n Edges in Cartesian tree are either disjoint or nested n n n 23 February 2006 So the interval tree has additional properties Operations are tailored to the special case of the Cartesian tree 23 rd International Symposium on Theoretical Aspects of Computer Science 18

Insertion once again 1. Find parent 3 b. Insert 3 1. Find parent 2. Edges affected 3 a. Delete 2 2. Edges affected 3 b. Insert 3 3 a. Delete 2 23 February 2006 4. Shrink k 23 rd International Symposium on Theoretical Aspects of Computer Science 19

Action implementations 1. Find parent n 23 February 2006 O(1)∗O(log n) Standard interval tree operations Shrink n O(log n+k) Special kind of stabbing query Insert and delete n 4. Uses the interval tree as a search tree Edges affected n 3. O(log n) k∗O(1) Emulating using inserts and deletes would yield O(k∗log n) Amortized argument based on the fact that shrinking edge travels down 23 rd International Symposium on Theoretical Aspects of Computer Science 20

Summary n Scheme for maintaining a Cartesian tree under insertion and week deletion Amortized O(log n) time per update n At any moment the actual tree structure is accessible n n Solution components Combinatorial analysis of tree behavior n Auxiliary data structure n n 23 February 2006 First result on dynamic Cartesian trees in a non-stochastic setting 23 rd International Symposium on Theoretical Aspects of Computer Science 21

Further work Strong deletion n Applications n n 23 February 2006 For example RMQ 23 rd International Symposium on Theoretical Aspects of Computer Science 22

Thank you! n 23 February 2006 Questions? 23 rd International Symposium on Theoretical Aspects of Computer Science 23