Stacks Chapter 6 The Abstract Data Type Stack

Stacks Chapter 6

The Abstract Data Type Stack • Operations on a stack o Last-in, o First-out behavior. • Applications demonstrated o Evaluating algebraic expressions o Searching for a path between two points

Developing an ADT During the Design of a Solution • Consider typing a line of text on a keyboard o Use of backspace key to make corrections o You type o Corrected input will be • Must decide how to store the input line.

Developing an ADT During the Design of a Solution • Initial draft of solution. • Two required operations ‒ Add new item to ADT ‒ Remove item added most recently

Developing an ADT During the Design of a Solution • Read and correct algorithm. • Third operation required ‒ See whether ADT is empty

Developing an ADT During the Design of a Solution • Write-backward algorithm • Fourth operation required ‒ Get item that was added to ADT most recently.

Specifications for the ADT Stack • See whether stack is empty. • Add new item to the stack. • Remove from and discard stack item that was added most recently. • Get copy of item that was added to stack most recently.

Specifications for the ADT Stack • FIGURE 6 -1 A stack of cafeteria plates LIFO: The last item inserted onto a stack is the first item out

Specifications for the ADT Stack • FIGURE 6 -2 UML diagram for the class Stack

Specifications for the ADT Stack • LISTING 6 -1 A C++ interface for stacks

Specifications for the ADT Stack • Axioms for multiplication • Axioms for ADT stack

Checking for Balanced Braces • Example of curly braces in C++ language o Balanced o Not balanced • Requirements for balanced braces o For each }, must match an already encountered { o At end of string, must have matched each {

Checking for Balanced Braces • Initial draft of a solution.

Checking for Balanced Braces • Detailed pseudocode solution.

Checking for Balanced Braces • FIGURE 6 -3 Traces of algorithm that checks for balanced braces

Recognizing Strings in a Language • Given a definition of a language, L o Special palindromes o Special middle character $ o Example ABC$CBA ɛ L, but AB$AB ɛ L • A stack is useful in determining whether a given string is in a language o Traverse first half of string o Push each character onto stack o Reach $, undo, pop character, match or not

Recognizing Strings in a Language • Algorithm to recognize string in language L

Using Stacks with Algebraic Expressions • Strategy o Develop algorithm to evaluate postfix o Develop algorithm to transform infix to postfix • These give us capability to evaluate infix expressions o This strategy easier than directly evaluating infix expression

Evaluating Postfix Expressions • Infix expression 2 * (3 + 4) • Equivalent postfix 2 3 4 + * o Operator in postfix applies to two operands immediately preceding • Assumptions for our algorithm o Given string is correct postfix o No unary, no exponentiation operators o Operands are single lowercase letters, integers

Evaluating Postfix Expressions • FIGURE 6 -4 The effect of a postfix calculator on a stack when evaluating the expression 2 * (3 + 4)

Evaluating Postfix Expressions • A pseudocode algorithm that evaluates postfix expressions

Infix to Postfix • Important facts o Operands always stay in same order with respect to one another. o Operator will move only “to the right” with respect to the operands; • If in the infix expression the operand x precedes the operator op, • Also true that in the postfix expression the operand x precedes the operator op. o All parentheses are removed.

Infix to Postfix • First draft of algorithm to convert infix to postfix

• Infix to Postfix Determining where to place operators in postfix expression o Parentheses o Operator precedence o Left-to-right association • Note difficulty o Infix expression not always fully parenthesized o Precedence and left-to-right association also affect results

Infix to Postfix • Figure 6 -5 A trace of the algorithm that converts the infix expression a − (b + c * d) /e to postfix form

Infix to Postfix • Pseudocode algorithm that converts infix to postfix

Using Stack to Search a Flight Map • FIGURE 6 -6 A flight map

Using Stack to Search a Flight Map • Recall recursive search strategy.

Using Stack to Search a Flight Map • Possible outcomes of exhaustive search strategy 1. 2. 3. Reach destination city, decide possible to fly from origin to destination Reach a city, C from which no departing flights You go around in circles • Use backtracking to recover from a wrong choice (2 or 3)

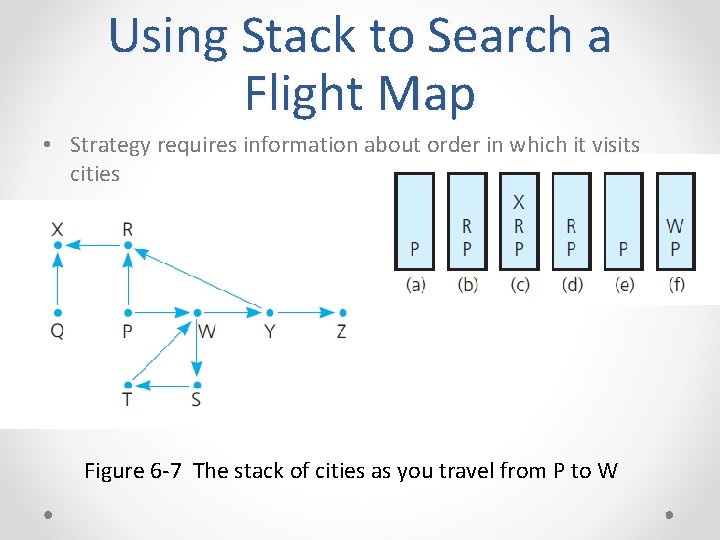
Using Stack to Search a Flight Map • Strategy requires information about order in which it visits cities Figure 6 -7 The stack of cities as you travel from P to W

Using Stack to Search a Flight Map • Stack will contain directed path from o Origin city at bottom to … o Current visited city at top • When to backtrack o No flights out of current city o Top of stack city already somewhere in the stack (already visited => acycle)

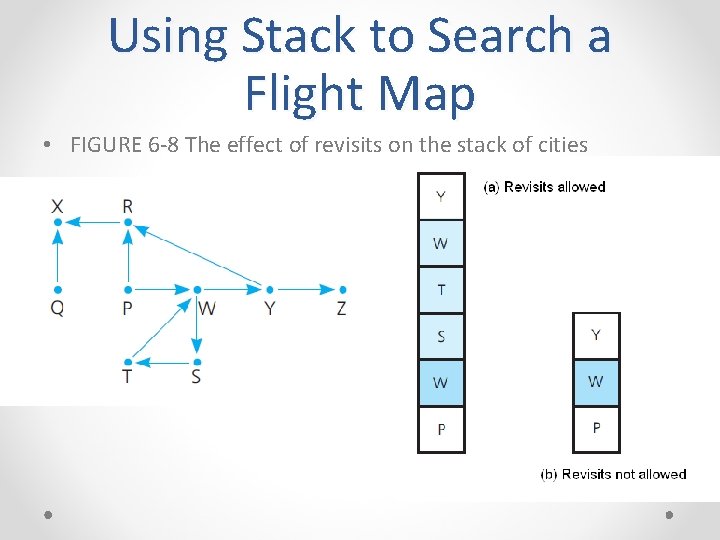
Using Stack to Search a Flight Map • FIGURE 6 -8 The effect of revisits on the stack of cities

Using Stack to Search a Flight Map • Final draft of algorithm.

Stack to Search a Flight Map • FIGURE 6 -9 A trace of search, given the flight map

Using Stack to Search a Flight Map • C++ implementation of search. S

Using Stack to Search a Flight Map • Figure 6 -10 Flight map for Checkpoint Question 8

Relationship Between Stacks and Recursion • Key aspects of common strategy o Visiting a new city o Backtracking o Termination

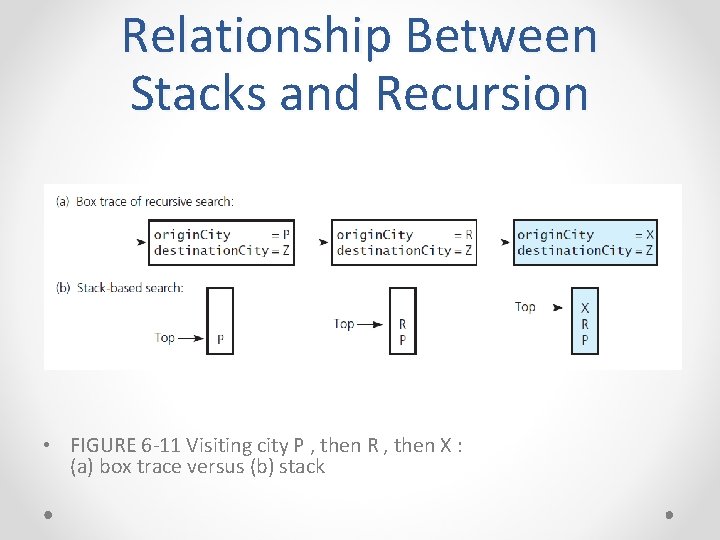
Relationship Between Stacks and Recursion • FIGURE 6 -11 Visiting city P , then R , then X : (a) box trace versus (b) stack

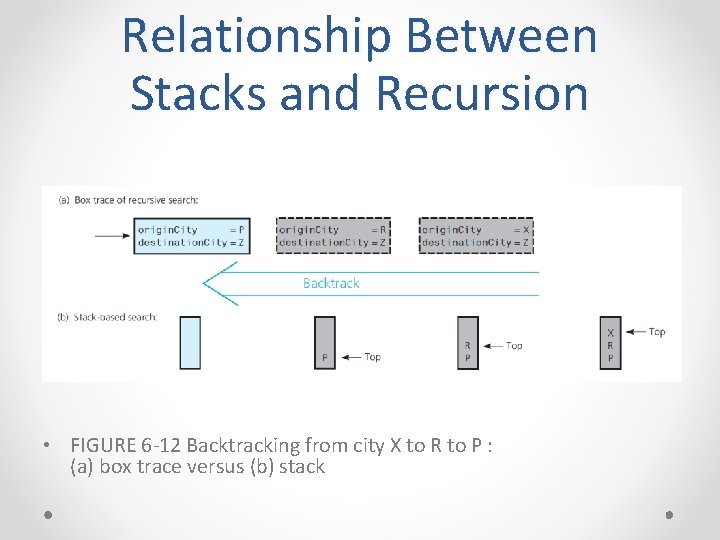
Relationship Between Stacks and Recursion • FIGURE 6 -12 Backtracking from city X to R to P : (a) box trace versus (b) stack

End Chapter 6