Stacks and Queues DSA 2013 Stacks n Queues

Stacks and Queues DSA 2013 Stacks n Queues

A Different Kind of Structure • There are significant differences between the data structures and algorithms of Arrays and that for Stacks & Queues. We’ll discuss three differences: 1. Programmer’s Tools • Arrays—as well as many other structures (linked lists, trees, etc. ) are appropriate for the kind of data you might find in a database application. • They’re typically used for personnel records, inventories, financial data, etc. —data that corresponds to real-world objects or activities. • These structures facilitate access to data: they make it easy to insert, delete, and search for particular items. DSA 2013 Stacks n Queues

A Different Kind of Structure • Stacks and Queues, on the other hand, are more often used as programmer’s tools. • They’re primarily conceptual aids rather than full-fledged data storage devices. • Their lifetime is typically shorter than that of the databasetype structures. • They are created and used to carry out a particular task during the operation of a program; when the task is completed, they’re discarded. DSA 2013 Stacks n Queues

A Different Kind of Structure 2. Restricted Access • In an array, any item can be accessed, either immediately—if its index number is known—or by searching through a sequence of cells until it’s found. • In Stacks and Queues, however, access is restricted: Only one item can be read or removed at a given time. 3. More Abstract • Stacks and queues are more abstract entities than arrays and many other data storage structures. The underlying mechanism used to implement them is typically not visible to their user. • The underlying mechanism for a stack, for example, can be an array or a linked list. The underlying mechanism for a priority queue can be an array or a special kind of tree called a heap. DSA 2013 Stacks n Queues

Stacks DSA 2013 Stacks n Queues

Abstract Data Types (ADTs) • An abstract data type (ADT) is an abstraction of a data structure • An ADT specifies: – Data stored – Operations on the data – Error conditions associated with operations DSA 2013 Stacks n Queues

Abstract Data Types (ADTs) • Example: ADT modeling a simple stock trading system – The data stored are buy/sell orders – The operations supported are • order buy(stock, shares, price) • order sell(stock, shares, price) • void cancel(order) – Error conditions: • Buy/sell a nonexistent stock • Cancel a nonexistent order DSA 2013 Stacks n Queues

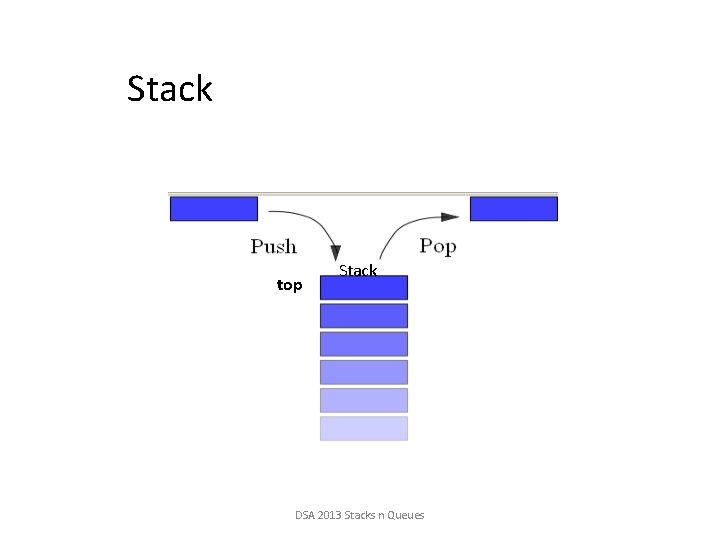
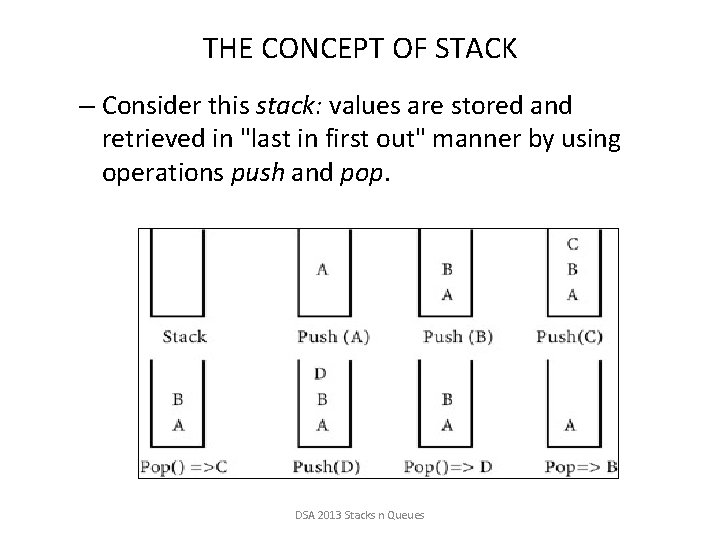
The Stack ADT • A stack is a list with the restriction – that insertions and deletions can only be performed at the top of the list • Stacks are less flexible ü but are more efficient and easy to implement • Stacks are known as LIFO (Last In, First Out) lists. – Insertions and deletions follow the last-in first-out scheme – The last element inserted will be the first to be retrieved DSA 2013 Stacks n Queues

The Stack ADT • Think of a spring-loaded plate dispenser • Main stack operations: – Push: inserts an element to the top of the stack – Pop: removes and returns the last inserted element • Auxiliary stack operations: – Top: returns the last inserted element without removing it – integer Size: returns the number of elements stored – boolean is. Empty: indicates whether no elements are stored DSA 2013 Stacks n Queues

Stack top Stack DSA 2013 Stacks n Queues

THE CONCEPT OF STACK – Consider this stack: values are stored and retrieved in "last in first out" manner by using operations push and pop. DSA 2013 Stacks n Queues

Exceptions • Attempting the execution of an operation may sometimes cause an error condition, called an exception • Exceptions are said to be “thrown” by an operation that cannot be executed • In the Stack ADT, operations pop and top cannot be performed if the stack is empty • Attempting the execution of pop or top on an empty stack throws an Empty. Stack. Exception DSA 2013 Stacks n Queues

Applications of Stacks • Direct applications – Page-visited history in a Web browser – Undo sequence in a text editor – Chain of Method calls in the Java Virtual Machine DSA 2013 Stacks n Queues

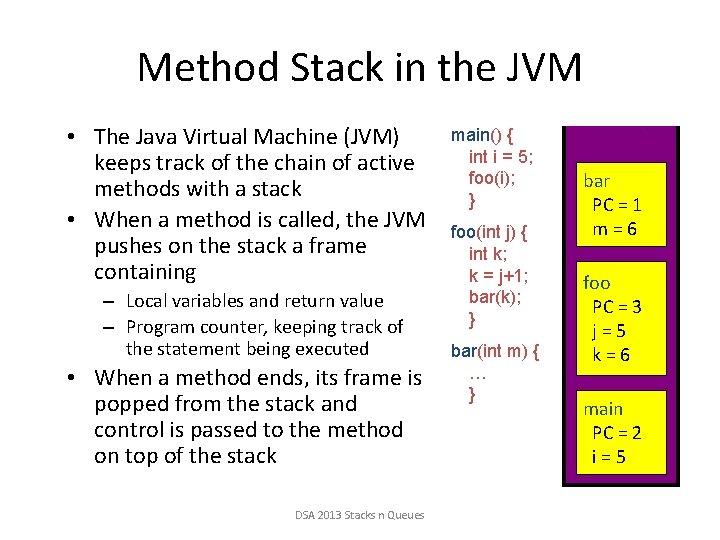
Method Stack in the JVM • The Java Virtual Machine (JVM) keeps track of the chain of active methods with a stack • When a method is called, the JVM pushes on the stack a frame containing – Local variables and return value – Program counter, keeping track of the statement being executed • When a method ends, its frame is popped from the stack and control is passed to the method on top of the stack DSA 2013 Stacks n Queues main() { int i = 5; foo(i); } foo(int j) { int k; k = j+1; bar(k); } bar(int m) { … } bar PC = 1 m=6 foo PC = 3 j=5 k=6 main PC = 2 i=5

Implementation of Stacks • need an underlying collection to hold the elements of the stack • 2 basic choices – Arrays (static: the size of stack is given initially) – Linked lists (dynamic: never become full) DSA 2013 Stacks n Queues

Array Implementation of Stack • A simple way of implementing the Stack ADT uses an array • Need to declare an array size ahead of time • A variable keeps track of the index of the top element, say, Top. Of. Stack – for an empty stack, set Top. Of. Stack to -1 • Push – (1) Increment Top. Of. Stack by 1. – (2) Set Stack[Top. Of. Stack] = X • Pop – (1) Set return value to Stack[Top. Of. Stack] – (2) Decrement Top. Of. Stack by 1 • These operations are performed in very fast constant time DSA 2013 Stacks n Queues

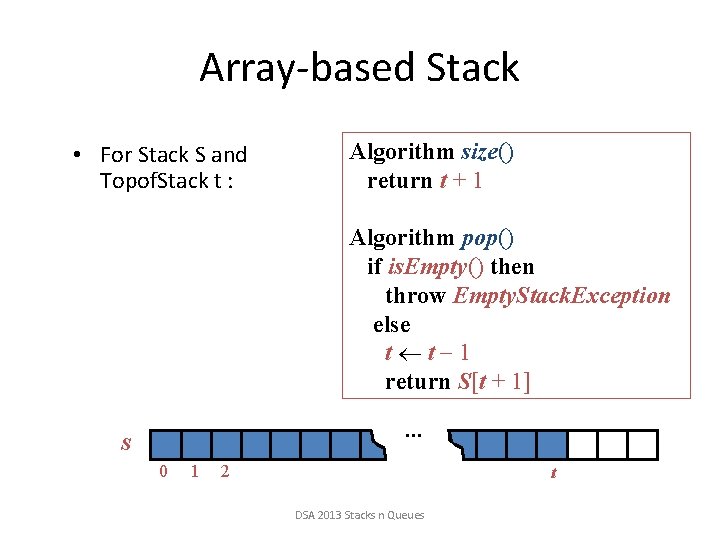
Array-based Stack • For Stack S and Topof. Stack t : Algorithm size() return t + 1 Algorithm pop() if is. Empty() then throw Empty. Stack. Exception else t t 1 return S[t + 1] … S 0 1 2 t DSA 2013 Stacks n Queues

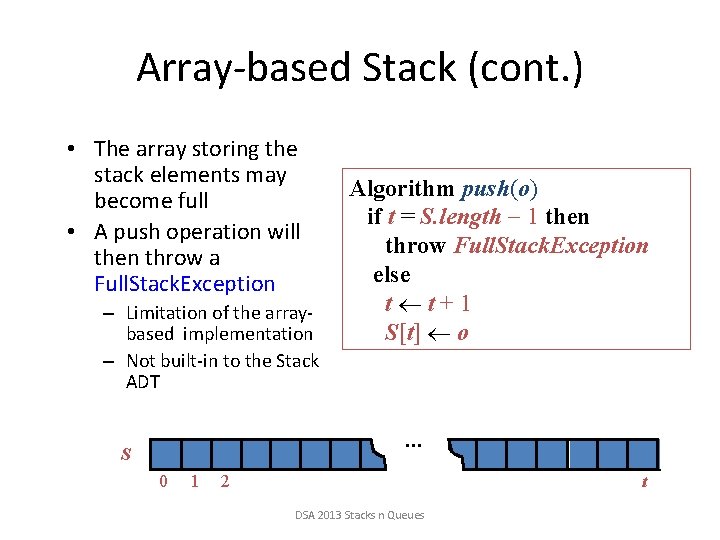
Array-based Stack (cont. ) • The array storing the stack elements may become full • A push operation will then throw a Full. Stack. Exception – Limitation of the arraybased implementation – Not built-in to the Stack ADT Algorithm push(o) if t = S. length 1 then throw Full. Stack. Exception else t t+1 S[t] o … S 0 1 2 t DSA 2013 Stacks n Queues

Performance and Limitations • Performance – Let n be the number of elements in the stack – The space used is O(n) – Each operation runs in constant time O(1) That is, the time is not dependent on how many items are in the stack and is therefore very quick. No comparisons or moves are necessary. • Limitations – The maximum size of the stack must be defined ahead of time and cannot be changed – Trying to push a new element into a full stack causes an implementation-specific exception DSA 2013 Stacks n Queues

Parentheses Matching • In processing programs and working with computer languages there are many instances when symbols must be balanced • Each “(”, “{”, or “[” must be paired with a matching “)”, “}”, or “[” – – correct: ( )(( )){([( )])} correct: ((( )){([( )])} incorrect: )(( )){([( )])} incorrect: ({[ ])} • A stack is useful for checking symbol balance. When a closing symbol is found it must match the most recent opening symbol of the same type. Algorithm? DSA 2013 Stacks n Queues

Algorithm for Balanced Symbol Checking • Make an empty stack • read symbols until end of file – if the symbol is an opening symbol push it onto the stack – if it is a closing symbol do the following • if the stack is empty report an error • otherwise pop the stack. If the symbol popped does not match the closing symbol report an error • At the end of the file if the stack is not empty report an error DSA 2013 Stacks n Queues

Parentheses Matching Algorithm Paren. Match(X, n): Input: An array X of n tokens, each of which is either a grouping symbol, a variable, an arithmetic operator, or a number Output: true if and only if all the grouping symbols in X match Let S be an empty stack for i=0 to n-1 do if X[i] is an opening grouping symbol then S. push(X[i]) else if X[i] is a closing grouping symbol then if S. is. Empty() then return false {nothing to match with} if S. pop() does not match the type of X[i] then return false {wrong type} if S. is. Empty() then return true {every symbol matched} else return false {some symbols were never matched} DSA 2013 Stacks n Queues

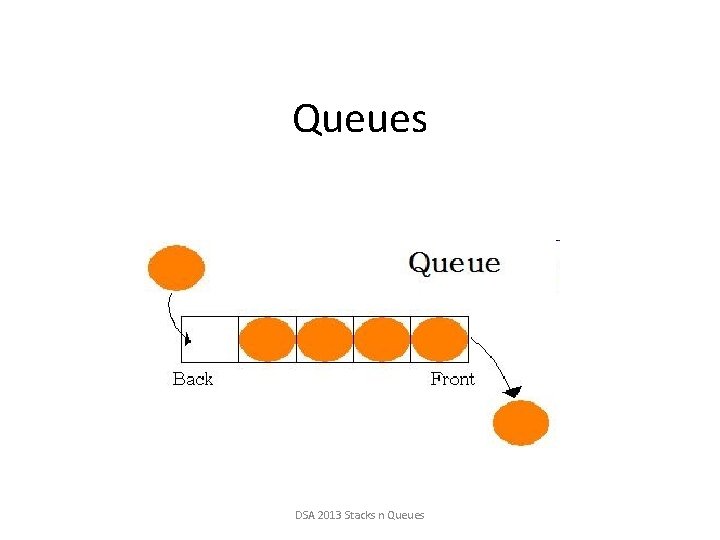
Queues DSA 2013 Stacks n Queues

Queue ADT • Like a stack, a queue is also a list. • However, with a queue, insertion is done at one end, while deletion is performed at the other end. • Accessing the elements of queues follows a First In, First Out (FIFO) order. – the first element added to the queue will be the first one to be removed – Like customers standing in a check-out line in a store, the first customer in is the first customer served. (or at a Bank) • Add items to the back (rear) of the queue • Access and remove from the front • Used extensively in operating systems – Queues of processes, I/O requests, and much more DSA 2013 Stacks n Queues

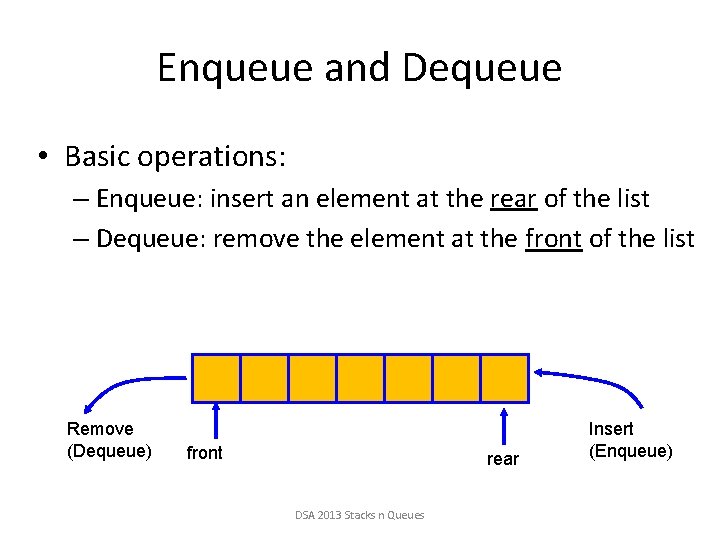
Enqueue and Dequeue • Basic operations: – Enqueue: insert an element at the rear of the list – Dequeue: remove the element at the front of the list Remove (Dequeue) front rear DSA 2013 Stacks n Queues Insert (Enqueue)

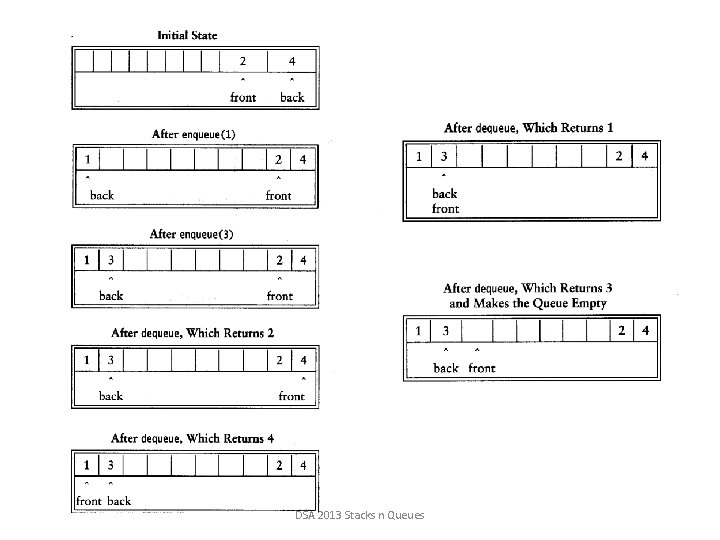
Queue Example Operation enqueue(5) enqueue(3) dequeue() enqueue(7) dequeue() front() dequeue() is. Empty() enqueue(9) enqueue(7) size() enqueue(3) enqueue(5) dequeue() Output Q – – 5 – 3 7 7 “error” true – – 2 – – 9 (5) (5, 3) (3, 7) (7) () (9) (9, 7) (9, 7, 3, 5) (7, 3, 5) DSA 2013 Stacks n Queues

Applications of Queues • Direct applications – Waiting lists, bureaucracy – Access to shared resources (e. g. , printer) – Multiprogramming DSA 2013 Stacks n Queues

Implementation of Queue • Just as stacks can be implemented as arrays or linked lists, so with queues. • Dynamic queues have the same advantages over static queues as dynamic stacks have over static stacks DSA 2013 Stacks n Queues

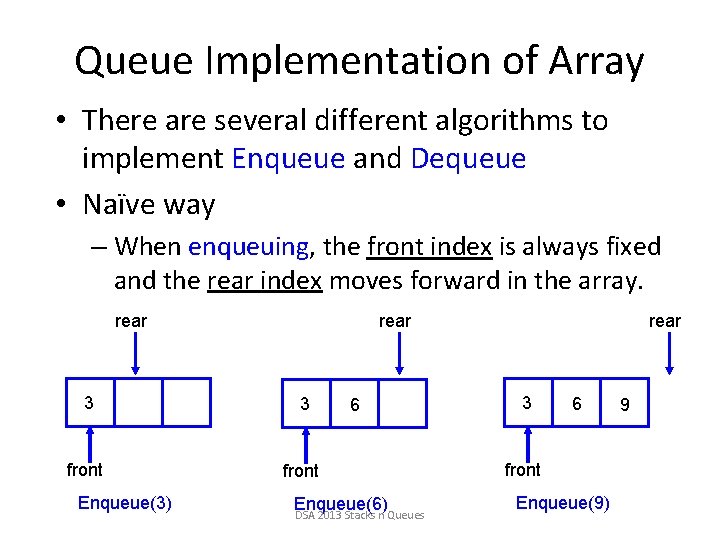
Queue Implementation of Array • There are several different algorithms to implement Enqueue and Dequeue • Naïve way – When enqueuing, the front index is always fixed and the rear index moves forward in the array. rear 3 3 front Enqueue(3) 6 Enqueue(6) DSA 2013 Stacks n Queues rear 3 6 front Enqueue(9) 9

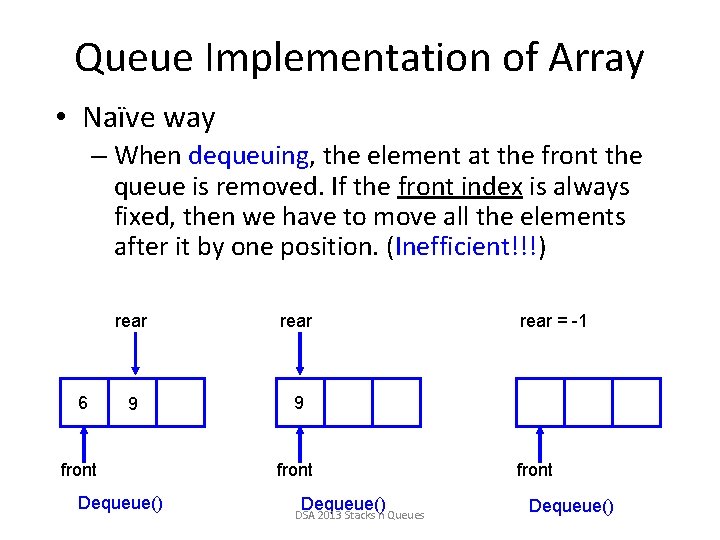
Queue Implementation of Array • Naïve way – When dequeuing, the element at the front the queue is removed. If the front index is always fixed, then we have to move all the elements after it by one position. (Inefficient!!!) 6 rear 9 9 front Dequeue() DSA 2013 Stacks n Queues rear = -1 front Dequeue()

Queue Implementation of Array • Better way • Instead, we keep the items in the same place and move the front and rear of the queue. (front) XXXXOOOOO OXXXXOOOO OOXXXXXOO OOOOXXXXX (rear) (after 1 dequeue, and 1 enqueue) (after 2 dequeues, and 3 enqueues) (after 4 dequeues, and 5 enqueues) • The trouble with this arrangement is that soon the rear of the queue is at the end of the array (the highest index). DSA 2013 Stacks n Queues

A Circular Queue • Even if there are empty cells at the beginning of the array, because you’ve removed them , you still can’t insert a new item because Rear can’t go any further. Wrapping around To avoid the problem of not being able to insert more items into the queue even when it’s not full, the Front and Rear arrows wrap around to the beginning of the array. • The result is a circular queue DSA 2013 Stacks n Queues

Implementation using Circular Array • Using a circular array • When an element moves past the end of a circular array, it wraps around to the beginning, e. g. – OOOOO 7963 4 OOOO 7963 (after Enqueue(4)) – After Enqueue(4), the rear index moves from pointing to 3 and points to 4. DSA 2013 Stacks n Queues

DSA 2013 Stacks n Queues

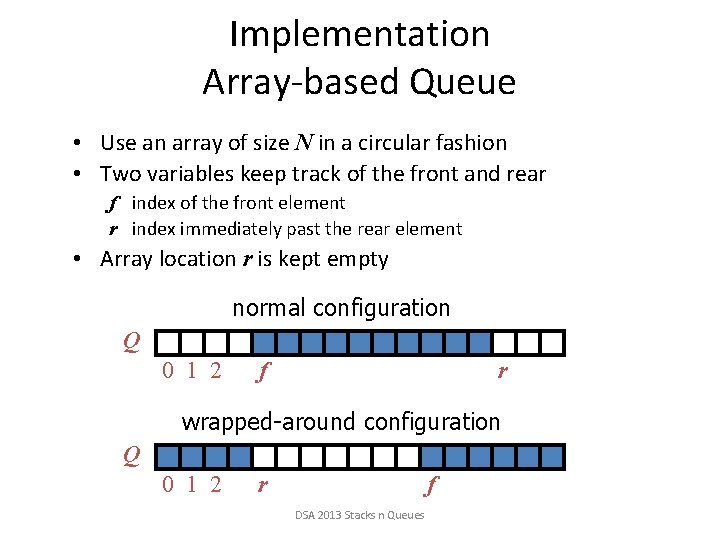
Implementation Array-based Queue • Use an array of size N in a circular fashion • Two variables keep track of the front and rear f index of the front element r index immediately past the rear element • Array location r is kept empty normal configuration Q 0 1 2 f r wrapped-around configuration Q 0 1 2 r f DSA 2013 Stacks n Queues

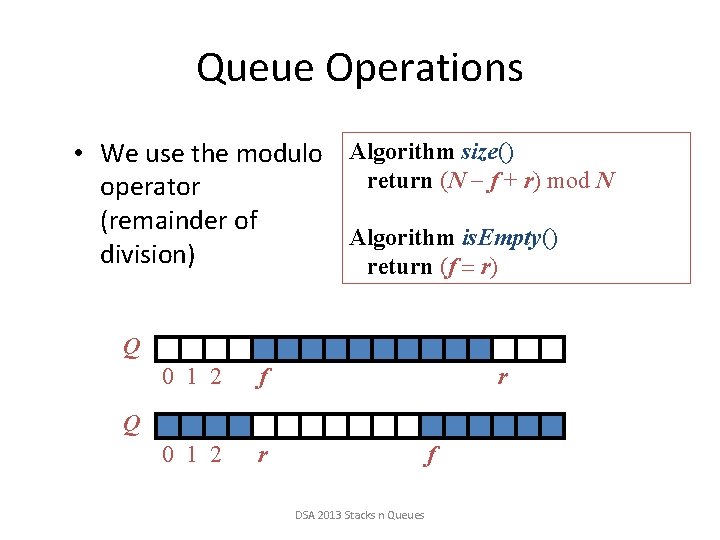
Queue Operations • We use the modulo Algorithm size() return (N f + r) mod N operator (remainder of Algorithm is. Empty() division) return (f = r) Q 0 1 2 f 0 1 2 r r Q f DSA 2013 Stacks n Queues

Queue Operations (cont. ) • Operation enqueue throws an exception if the array is full • This exception is implementationdependent Algorithm enqueue(o) if size() = N 1 then throw Full. Queue. Exception else Q[r] o r (r + 1) mod N Q 0 1 2 f 0 1 2 r r Q f DSA 2013 Stacks n Queues

Queue Operations (cont. ) • Operation dequeue throws an exception if the queue is empty • This exception is specified in the queue ADT Algorithm dequeue() if is. Empty() then throw Empty. Queue. Exception else o Q[f] f (f + 1) mod N return o Q 0 1 2 f 0 1 2 r r Q f DSA 2013 Stacks n Queues

Deques • A deque is a double-ended queue. • You can insert items at either end and delete them from either end. The methods might be called insert. Left() and insert. Right(), and remove. Left() and remove. Right(). • If you restrict yourself to insert. Left() and remove. Left() (or their equivalents on the right), the deque acts like a stack. If you restrict yourself to insert. Left() and remove. Right() (or the opposite pair), it acts like a queue. • A deque provides a more versatile data structure than either a stack or a queue. However, it’s not used as often as stacks and queues, so we won’t explore it further. DSA 2013 Stacks n Queues

Priority Queues • A priority queue is a more specialized data structure than a stack or a queue. • Like an ordinary queue, a priority queue has a front and a rear, and items are removed from the front. • However, in a priority queue, items are ordered by key value so that the item with the lowest key (or the highest key) is always at the front. • Items are inserted in the proper position to maintain the order. DSA 2013 Stacks n Queues

Priority Queue Implementation • A priority queue can be implemented by a sorted array or a special kind of tree called a heap (we’ll see this later). • Performance: – insert takes O(n) time since we have to find the place where to insert the item – delete takes O(1) time, since the smallest key is at the beginning DSA 2013 Stacks n Queues

Priority Queue Applications • Like stacks and queues, priority queues are often used as programmer’s tools. We’ll see one used in finding something called a minimum spanning tree for a graph later Priority-based OS process scheduler • Priority queues are used in various ways in certain computer systems. In a multitasking operating system, for example, programs may be placed in a priority queue so the highest-priority program is the next one to execute. DSA 2013 Stacks n Queues

Efficiency of Stacks & Queues • Items can be both pushed and popped from the stack in constant O(1) time. That is, the time is not dependent on how many items are in the stack and is therefore very quick. No comparisons or moves are necessary. • As with a stack, items can be inserted and removed from a queue in O(1) time. DSA 2013 Stacks n Queues