stacking of semiquinone radicals determines magnetic and electrical

π-stacking of semiquinone radicals determines magnetic and electrical properties of crystals Krešimir Molčanov, Ana Šantić, Vladimir Stilinović, Biserka Kojić-Prodić, Dietmar Stalke, Bruno Landeros-Rivera, Jesús Hernández-Rivera, Miklosz Kertesz, Zhongyu Mou

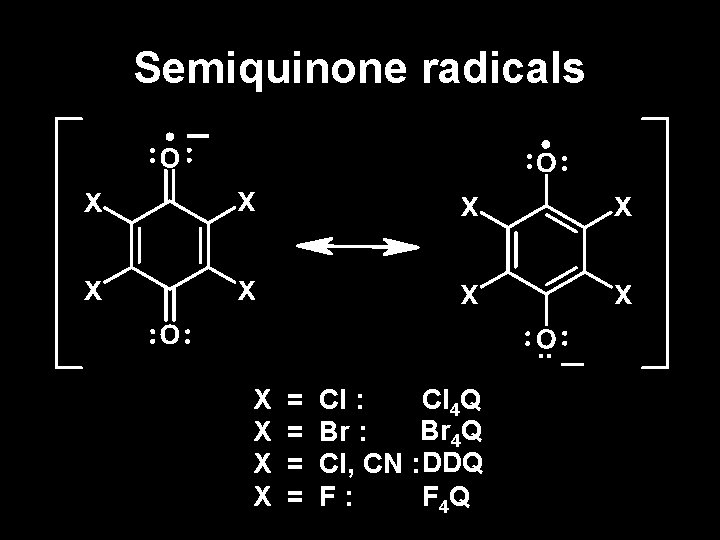
Semiquinone radicals . . X X = = Cl : Cl 4 Q Br : Cl, CN : DDQ F: F 4 Q

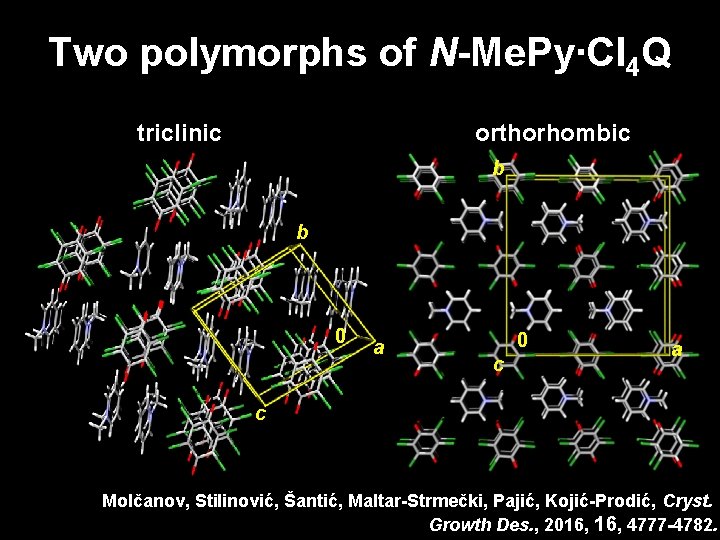
Two polymorphs of N-Me. Py∙Cl 4 Q triclinic orthorhombic b b 0 a 0 c a c Molčanov, Stilinović, Šantić, Maltar-Strmečki, Pajić, Kojić-Prodić, Cryst. Growth Des. , 2016, 4777 -4782.

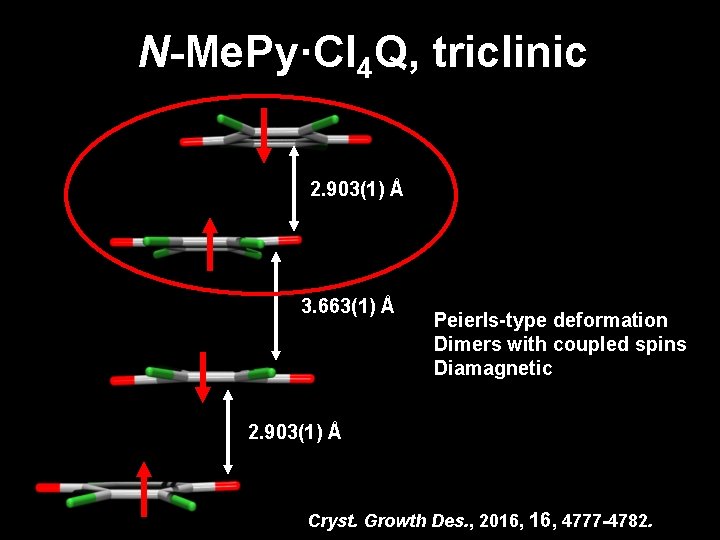
N-Me. Py·Cl 4 Q, triclinic 2. 903(1) Å 3. 663(1) Å Peierls-type deformation Dimers with coupled spins Diamagnetic 2. 903(1) Å Cryst. Growth Des. , 2016, 4777 -4782.

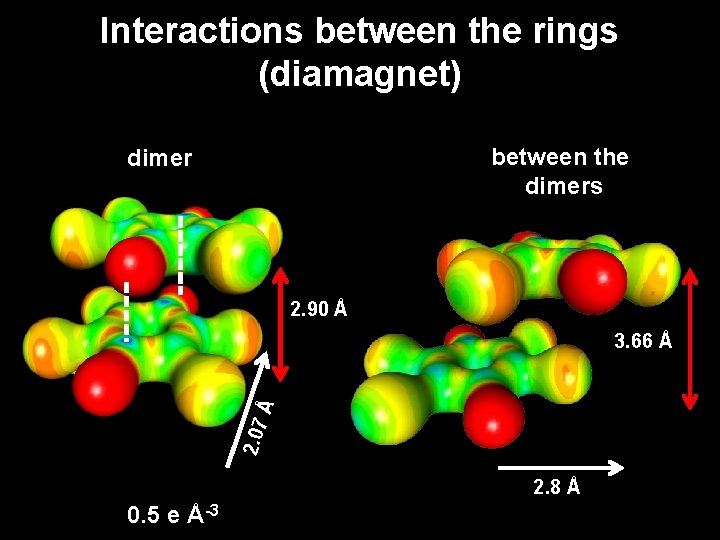
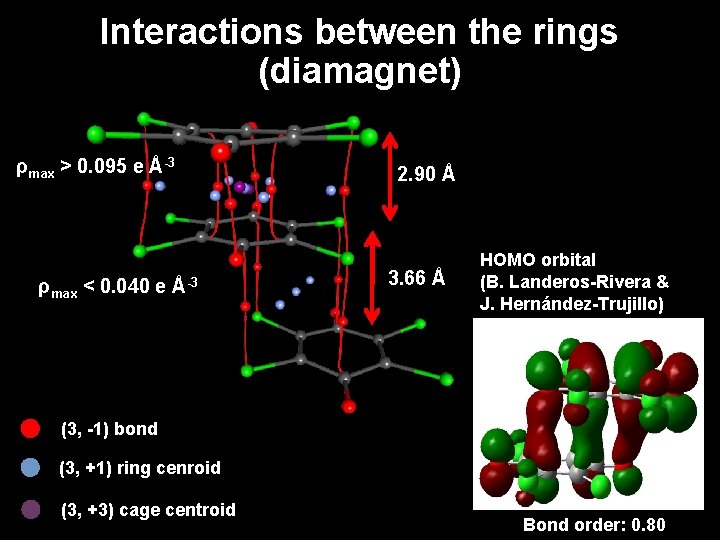
Interactions between the rings (diamagnet) between the dimers dimer 2. 90 Å 2. 07 Å 3. 66 Å 2. 8 Å 0. 5 e Å-3

Interactions between the rings (diamagnet) ρmax > 0. 095 e Å-3 ρmax < 0. 040 e Å-3 2. 90 Å 3. 66 Å HOMO orbital (B. Landeros-Rivera & J. Hernández-Trujillo) (3, -1) bond (3, +1) ring cenroid (3, +3) cage centroid Bond order: 0. 80

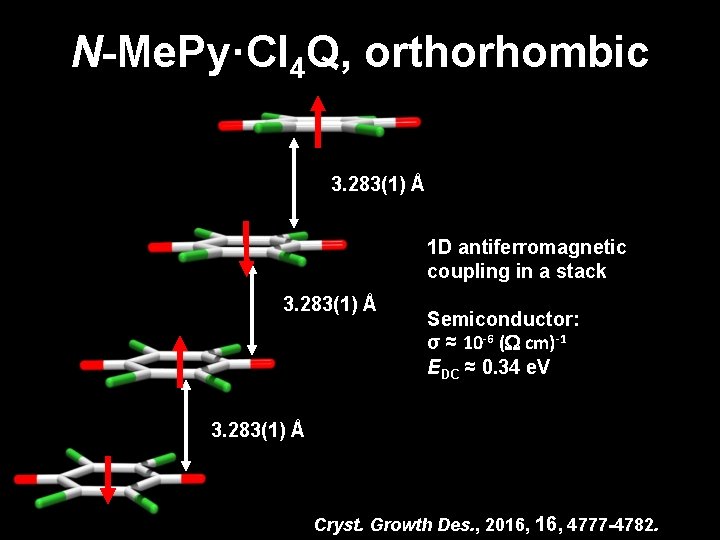
N-Me. Py·Cl 4 Q, orthorhombic 3. 283(1) Å 1 D antiferromagnetic coupling in a stack 3. 283(1) Å Semiconductor: σ ≈ 10 -6 ( cm)-1 EDC ≈ 0. 34 e. V 3. 283(1) Å Cryst. Growth Des. , 2016, 4777 -4782.

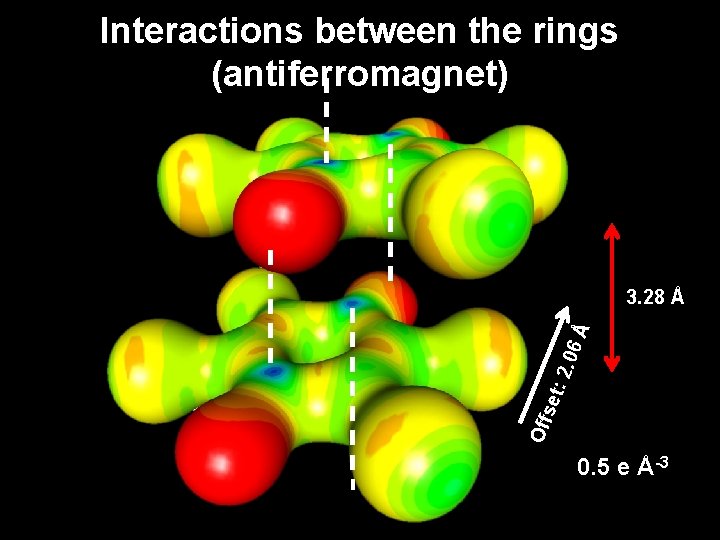
Interactions between the rings (antiferromagnet) Off set : 2. 06 Å 3. 28 Å 0. 5 e Å-3

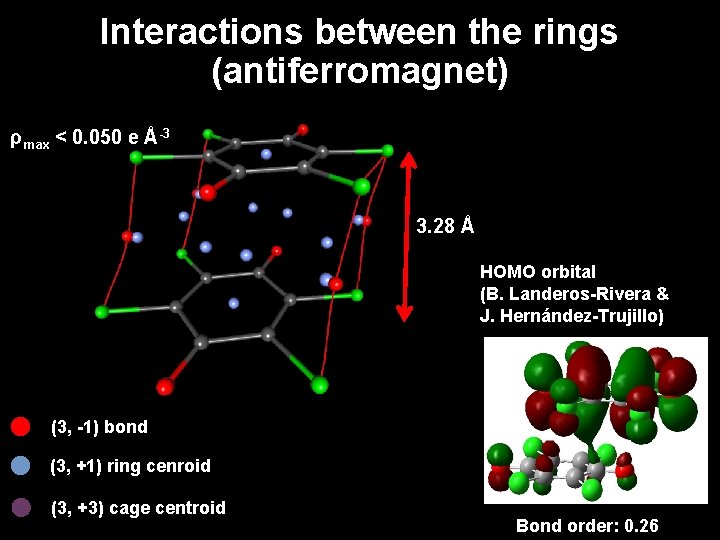
Interactions between the rings (antiferromagnet) ρmax < 0. 050 e Å-3 3. 28 Å HOMO orbital (B. Landeros-Rivera & J. Hernández-Trujillo) (3, -1) bond (3, +1) ring cenroid (3, +3) cage centroid Bond order: 0. 26

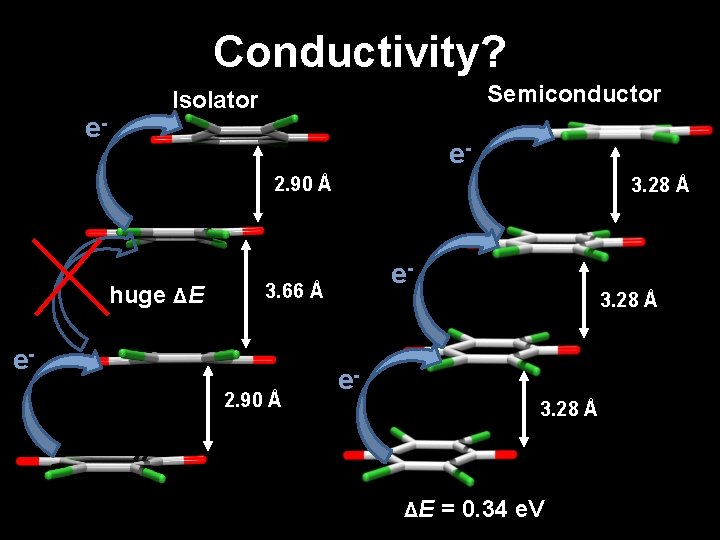
Conductivity? e- Semiconductor Isolator e 2. 90 Å huge ΔE 3. 28 Å e- 3. 66 Å e 2. 90 Å 3. 28 Å e 3. 28 Å ΔE = 0. 34 e. V

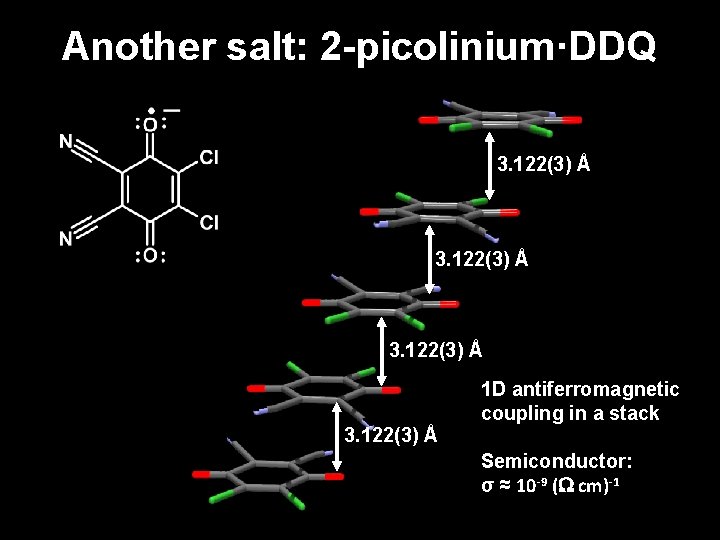
Another salt: 2 -picolinium·DDQ 3. 122(3) Å 1 D antiferromagnetic coupling in a stack Semiconductor: σ ≈ 10 -9 ( cm)-1

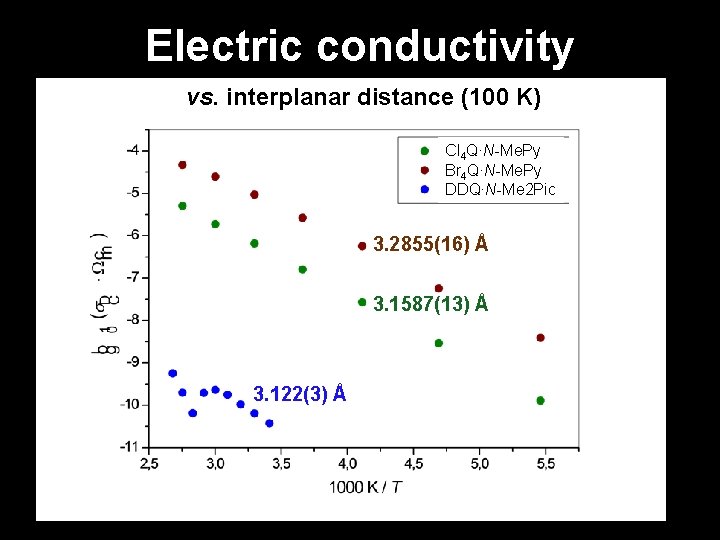
Electric conductivity vs. interplanar distance (100 K) Cl 4 Q∙N-Me. Py Br 4 Q∙N-Me. Py DDQ∙N-Me 2 Pic 3. 2855(16) Å 3. 1587(13) Å 3. 122(3) Å

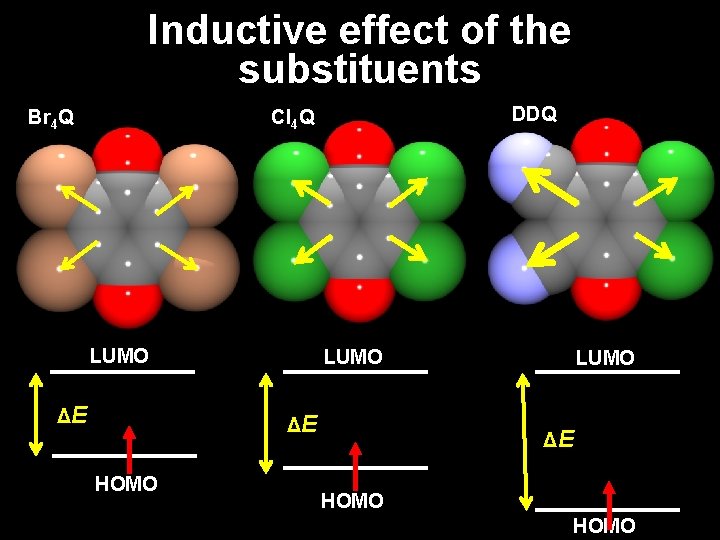
Inductive effect of the substituents DDQ Cl 4 Q Br 4 Q LUMO ΔE HOMO

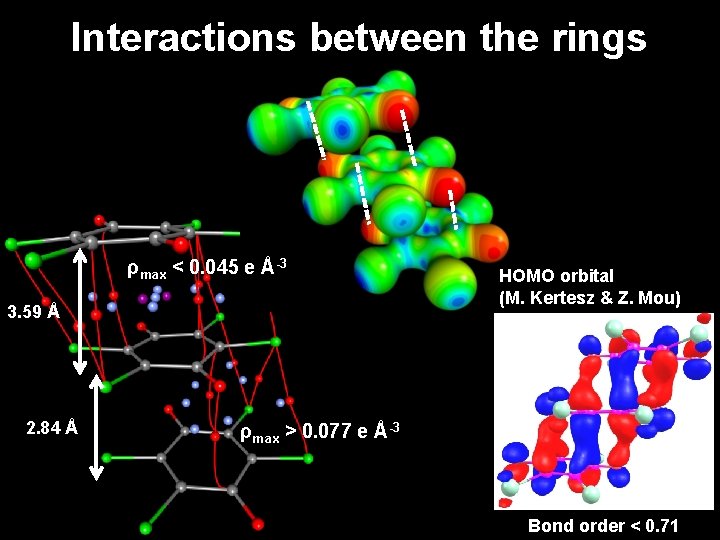
[N-Me-4 -(Me)2 NPy]2(Cl 4 Q)3 A charge-transfer complex 2. 84 Å 1. 32 Å 3. 59 Å ≈1. 76 Å

[N-Me-4 -(Me)2 NPy]2(Cl 4 Q)3 A charge-transfer complex – 0, 58 Charges derived from Pval: – 1. 92 +0. 96 – 0, 76 – 0, 58 +0. 96 2– 1+ 1+

Interactions between the rings ρmax < 0. 045 e Å-3 3. 59 Å 2. 84 Å HOMO orbital (M. Kertesz & Z. Mou) ρmax > 0. 077 e Å-3 Bond order < 0. 71

Conclusions • energy of interaction exceeds 15 kcal mol-1 • dominant interaction is weak covalent („pancake bonding”) • secondary: electrostatic (offset) • possible electron transfer between the rings: semiconductivity • magnetic properties can be tuned by tuning geometry of stacking

Acknowlegdements Thank you for your attention! RBI, Zagreb Marijana Jurić Lidija Androš Dubraja Nadica Maltar-Strmečki Dijana Žilić University of Zagreb Damir Pajić Nikolina Novosel Krešo Zadro Georgetown University Miklosz Kertesz Zhongyu Mou Université de Lorraine Claude Lecomte Christian Jelsch Emmanuel Wenger Rigaku Oxford Diffraction Ltd. Marcus Winter Dyanne Cruikshank Universität Göttingen Dietmar Stalke Serhey Demeshko UNAM, Mexico City Bruno Landeros-Rivera Jesús Hernández-Trujillo Croatian Science Foundation, grant no. IP-2014 -09 -4079 Croatian Academy of Sciences and Arts French-Croatian bilateral, Slovenian-Croatian bilateral German-Croatrian bilateral