STACK Yohana Nugraheni Pengertian STACK l l STACK

STACK Yohana Nugraheni

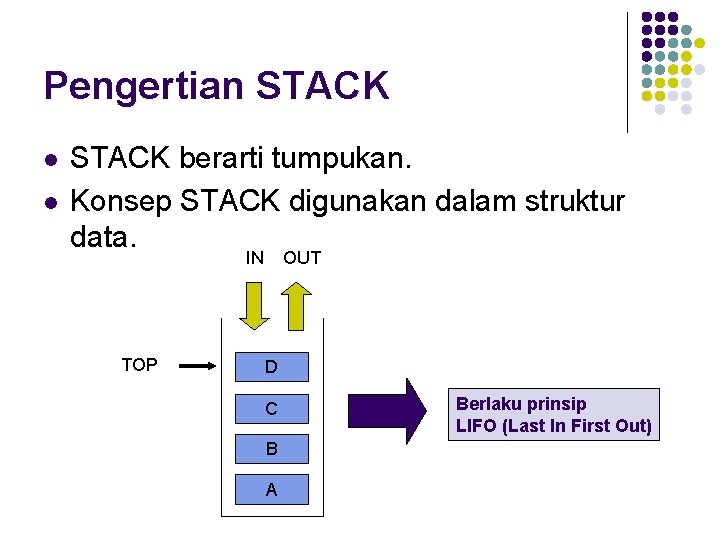
Pengertian STACK l l STACK berarti tumpukan. Konsep STACK digunakan dalam struktur data. IN TOP OUT D C B A Berlaku prinsip LIFO (Last In First Out)

Pengertian STACK l Dalam Struktur Stack digunakan istilah : l l l PUSH : Simpan, Masuk, Insert, Tulis POP : Ambil, Keluar, Delete, Baca STACK ada 2 jenis : l l Single Stack Double Stack

Single Stack l Single Stack dapat direpresentasikan menggunakan array satu dimensi. 0 S[10] 1 2 3 4 5 25 12 17 15 33 TOP 4 33 TOP X 6 7 8 9

Prinsip dan Konsep Proses Single Stack l Prinsip proses Single Stack adalah : LIFO (Last In First Out) l Proses pada Single Stack : l AWAL (Inisialisasi) l PUSH (Insert, Masuk, Simpan, Tulis) l POP (Delete, Keluar, Ambil, Baca/Hapus)

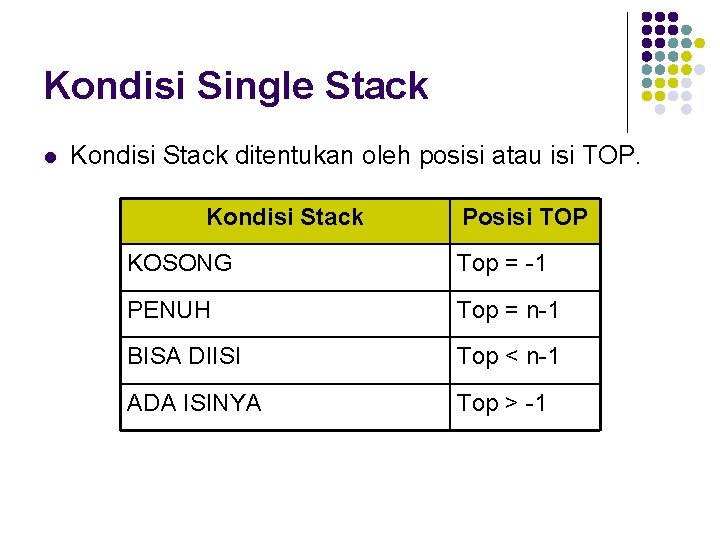
Kondisi Single Stack l Kondisi Stack ditentukan oleh posisi atau isi TOP. Kondisi Stack Posisi TOP KOSONG Top = -1 PENUH Top = n-1 BISA DIISI Top < n-1 ADA ISINYA Top > -1

Algoritma PUSH if (Top < n-1) { Top = Top + 1; S[Top] = x; } else cout<<“Stack Penuh”;

Algoritma POP if (Top > -1) { x = S[Top]; Top = Top - 1; } else cout<<“Stack Kosong”;

Contoh: PUSH Stack sampai penuh kemudian POP isi Stack sampai kosong l l l Buat program untuk menyiapkan array satu dimensi yang akan digunakan untuk mengisi Stack S sebanyak 5 elemen, bertipe integer. Input data dan PUSH ke Stack S. Proses input akan selesai setelah Stack penuh atau data yang diinputkan = 999. POP isi Stack kemudian cetak ke layar.

Double Stack l Disebut juga Stack Ganda. Stack 1 -1 S[12] 0 1 Stack 2 2 3 4 5 6 7 8 25 12 17 9 50 44 TOP 2 TOP 1 2 8 TOP 1 TOP 2 X 10 11 12 6 23

Prinsip dan Konsep Proses Double Stack l Prinsip proses : LIFO (Last In First Out) baik untuk Stack 1 maupun untuk Stack 2 l Proses pada Double Stack : l AWAL (Inisialisasi) l PUSH 1 (Push untuk Stack 1) l POP 1 (Pop untuk Stack 1) l PUSH 2 (Push untuk Stack 2) l POP 2 (Pop untuk Stack 2)

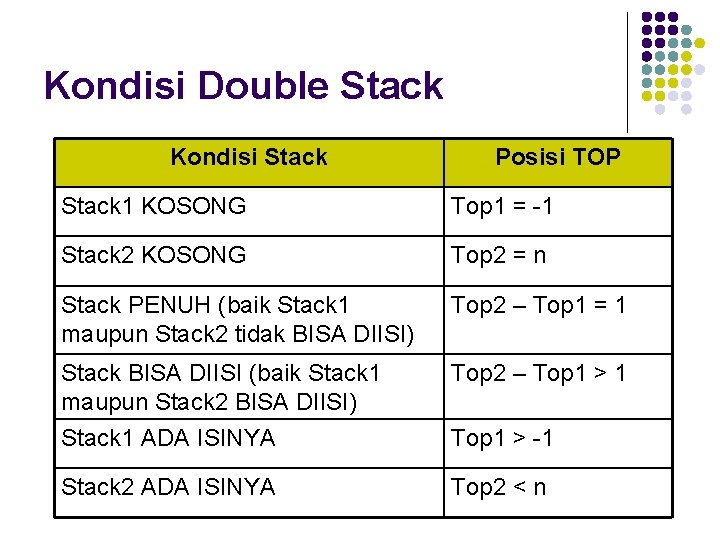
Kondisi Double Stack Kondisi Stack Posisi TOP Stack 1 KOSONG Top 1 = -1 Stack 2 KOSONG Top 2 = n Stack PENUH (baik Stack 1 maupun Stack 2 tidak BISA DIISI) Top 2 – Top 1 = 1 Stack BISA DIISI (baik Stack 1 maupun Stack 2 BISA DIISI) Stack 1 ADA ISINYA Top 2 – Top 1 > 1 Stack 2 ADA ISINYA Top 2 < n Top 1 > -1

Algoritma PUSH 1 (mengisi Stack 1) l Periksa apakah Stack 1 BISA DIISI if (Top 2 – Top 1 > 1) { Top 1 = Top 1 + 1; S[Top 1] = x; } else cout<<“Stack Penuh”;

Algoritma POP 1 (mengambil isi Stack 1) l Periksa apakah Stack 1 ADA ISINYA if (Top 1 > -1) { x = S[Top 1]; Top 1 = Top 1 - 1; } else cout<<“Stack Kosong”;

Algoritma PUSH 2 (mengisi Stack 2) l Periksa apakah Stack 2 BISA DIISI if (Top 2 – Top 1 > 1) { Top 2 = Top 2 - 1; S[Top 2] = x; } else cout<<“Stack Penuh”;

Algoritma POP 2 (mengambil isi Stack 2) l Periksa apakah Stack 2 ADA ISINYA if (Top 2 < n) { x = S[Top 2]; Top 2 = Top 2 + 1; } else cout<<“Stack Kosong”;