Stack Pendahuluan Stack Tumpukan piring tumpukan kertas tumpukan

Stack

Pendahuluan Stack • Tumpukan piring, tumpukan kertas, tumpukan batu, dlsb • Dalam kehidupan sehari-hari sering kita menjumpai tumpukan • Sifat tumpukan : satu elemen tumpukan dapat diambil bila tumpukan di atasnya dapat diambil

Pendahuluan Stack • Elemen terakhir yang ditumpuk, yang akan diambil untuk yang pertama. • Sifat ini disebut : LIFO Last In First Out • Untuk tumpukan tertentu ada yang khusus elemen tumpukan hanya boleh diambil satu persatu

Pendahuluan Stack • Pada dunia komputer, konsep tumpukan sering digunakan • Sifat tumpukannya hanya boleh diambil satu per satu • Contoh : – Penanganan pemanggilan sub program saat pelaksanaan suatu program – Evaluasi pernyataan aritmatika

Pendahuluan Stack • Ada dua operasi dasar pada tumpukan : – Tumpuk – Ambil

Implementasi dengan larik Max. tumpukan atas tumpukan

Implementasi dengan larik def maks. Tumpukan : 20 Tumpukan : array[1. . maks. Tumpukan] of string atas : integer edef

Operasi tumpuk data • Operasi pertama : tumpuk data proc tumpuk {tumpuk data x pada tumpukan dan laporkan apakah penuh atau tidak} if atas == maks. Tumpukan then penuh = true else atas = atas + 1 tumpukan[atas] = x penuh = false eif eproc

Operasi ambil data • Operasi ambil data proc Jumput(x, kosong) {ambil elemen teratas tumpukan lalu simpan pada x dan laporkan apakah kosong atau tidak} if atas == 0 then kosong = true else x = tumpukan[atas] atas = atas - 1 kosong = false eif eproc

Evaluasi Bentuk Postfix • Suatu pernyataan aritmatika terdiri dari sejumlah operator dan operand • Operator dapat terdiri dari : +, -, *, / dll • Operand : bilangan atau variabel

Evaluasi Bentuk Postfix • Setiap pernyataan aritmatika dapat dinyatakan dalam bentuk : – Infix – Prefix – Postfix : 2+3 : 23+ : +23

Evaluasi Bentuk Postfix • 2 4 6 * + : akan menghasilkan nilai = 26 • Algoritmanya : Ambil satu operator while ada operator do Operasikan terhadap dua operand disebelah kirinya, dan hasilnya membentuk operand baru Ambil operator berikutnya ewhile

Evaluasi Bentuk Postfix • Kelompok aksara yang dianggap satu kesatuan disebut token • Token : – Operator – Operand – Tanda sama dengan pernyataan merupakan akhir dari

Evaluasi Bentuk Postfix • Modul : Operasikan terhadap dua operand disebelah kirinya, dan hasilnya membentuk operand baru merupakan operasi pada tumpukan • Setiap kali menemukan operand, ditumpuk pada tumpukan

Evaluasi Bentuk Postfix • Modul : Pengoperasian dua operand disebelah kiri operator sama dengan pengoperasian dua operand teratas pada tumpukan. • Hasilnya ditaruh lagi pada tumpukan. • Hasil akhir dari pengevaluasian adalah elemen teratas pada tumpukan.

Isi Tumpukan Isi OP 1 Tumpukan Pernyataan yang akan dikerjakan OP 2 2 3 += += = 2 23 2 2 5 3 3

Pernyataan yang akan dikerjakan Isi Tumpukan Isi OP 1 Tumpukan OP 2 246*+= += += += = 2 24 246 24 2 26 4 6 6 2 24 24

Pernyataan yang akan dikerjakan Isi Tumpukan Isi OP 1 Tumpukan OP 2 2 4 + 6 * 15 3 -/= 6 * 15 3 -/= 15 3 -/= 2 24 2 2 4 4 6 6 66 6 36

Pernyataan yang akan dikerjakan 3 -/= Isi Tumpukan Isi OP 1 Tumpukan OP 2 36 15 -/= 36 15 3 /= /= /= = 36 15 36 36 12 36 3 15 3 3 36 12 12

Algoritma Global Ambil. Token (token, operand, operator) while token < > tanda. Sama. Dengan do if token = simbol. Operand then Tumpuk (operand, penuh) else (token adalah operator) Jumput (op 1, kosong) Jumput (op 2, kosong)

Algoritma Global Tumpuk (Evaluasi (op 2, op 1, operator), tumpukan) Eif Ambil. Token(token, operand, operator) ewhile

Pengembangan Algoritma prog Evaluasi. Postfix () read(pernyataan) Ambil. Token (token, operand, operator) while token < > tanda. Sama. Dengan do case token of

Pengembangan Algoritma simbol. Operand: Tumpuk (operand, penuh) If penuh then Henti(‘Pernyataan terlalu panjang’)

Pengembangan Algoritma simbol. Operator: Jumput(op 1, kosong) if kosong then Henti (‘Kurang operand’) Jumput (op 2, kosong) if kosong then Henti (‘Kurang operand’) Tumpuk (Evaluasi (op 2, op 1, operator), penuh)

Pengembangan Algoritma Simbol. Absah: Henti (‘Aksara tidak dikenal) Simbol. Kosong: (‘Pernyataan tidak lengkap’) ecase Ambil. Token (token, operand, operator) ewhile

Pengembangan Algoritma {Periksa keadaan akhir tumpukan dan tuliskan hasilnya} case atas of 0: write (‘Pernyataan kosong’) 1: write (tumpukan[atas]) else write (‘Kurang Operator’) ecase eprog

Deskripsi masing-masing modul • Ambil. Token (token, operand, operator): – Mengambil satu token – Token dapat berupa : • Simbol operand • Simbol operator • Tanda sama dengan • Aksara absah • Simbol Kosong

Deskripsi masing-masing modul Ambil. Token (token, operand, operator): – Simbol operand variabel operand – Simbol operator variabel operator

Deskripsi masing-masing modul • Tumpuk (operand, penuh) – Menaruh operand pada tumpukan – Melaporkan tumpukan penuh/tidak – Penuh variabel penuh benar – Bila tidak variabel penuh salah

Deskripsi masing-masing modul • Henti (pesan): – Menghentikan program sambil memperagakan pesan

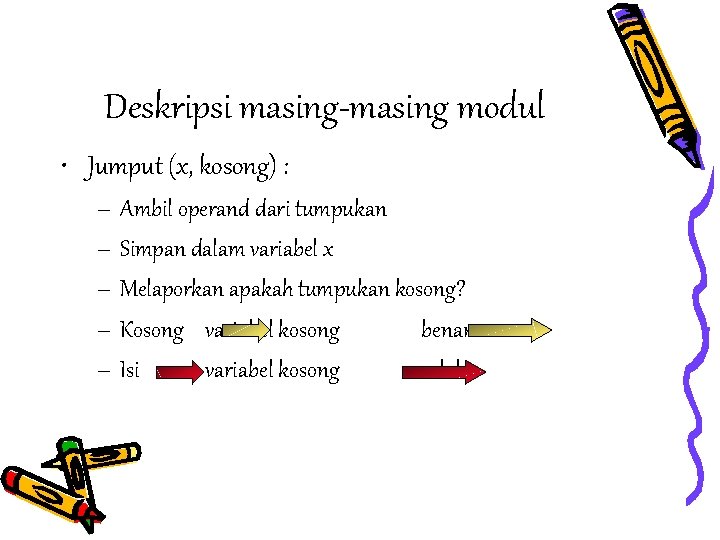
Deskripsi masing-masing modul • Jumput (x, kosong) : – Ambil operand dari tumpukan – Simpan dalam variabel x – Melaporkan apakah tumpukan kosong? – Kosong variabel kosong benar – Isi variabel kosong salah

Deskripsi masing-masing modul • Evaluasi (op 1, op 2, operator) – Mengembalikan hasil evaluasi operand op 1 dengan operand op 2 menggunakan operator

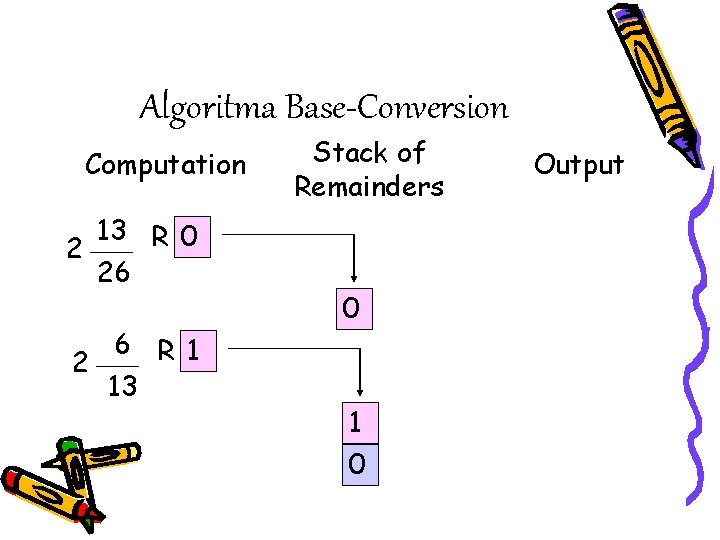
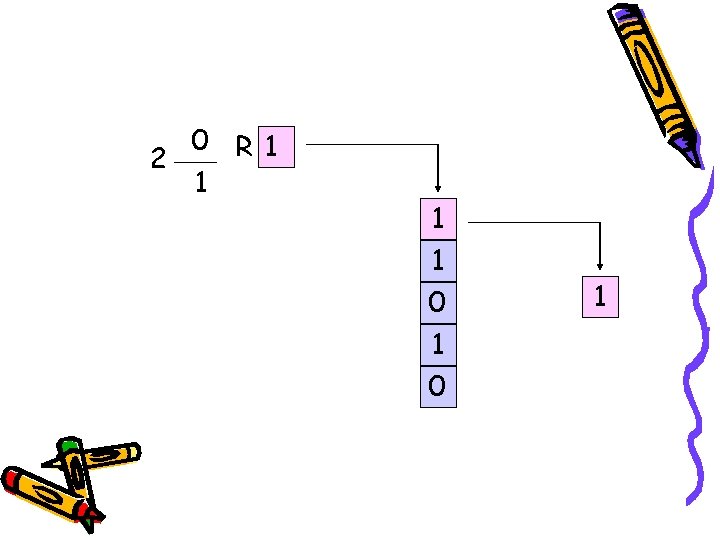
Algoritma Base-Conversion • Mengkonversi nilai basis 10 ke basis 2

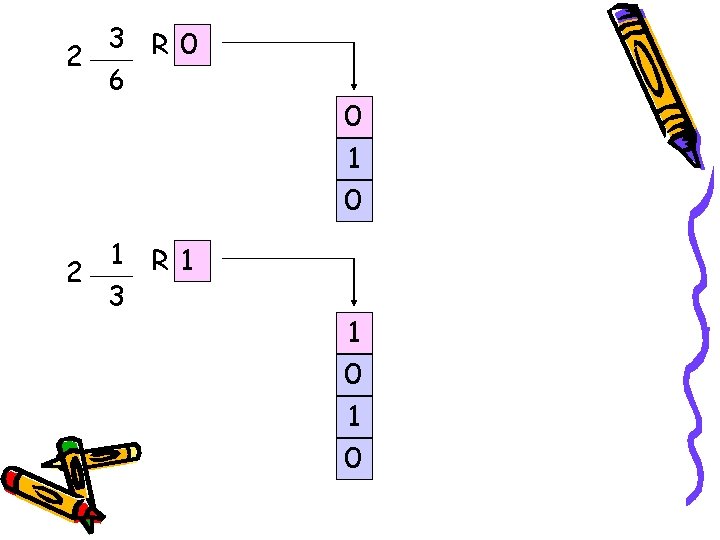
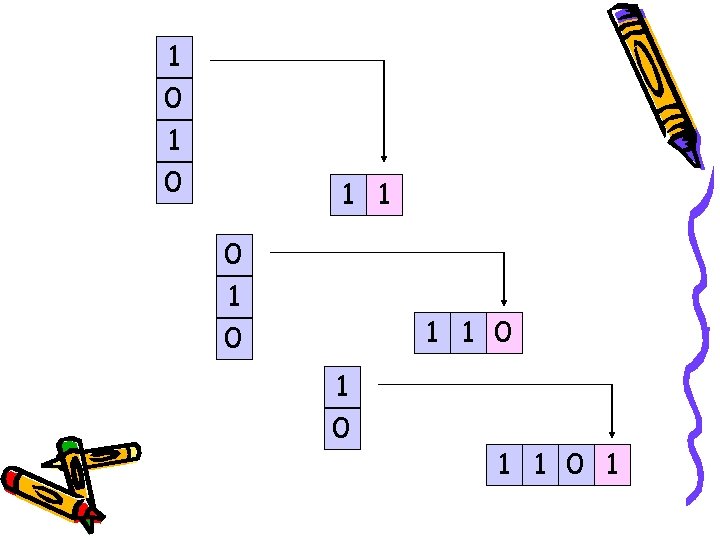
Algoritma Base-Conversion Computation 13 R 0 2 26 6 R 1 2 13 Stack of Remainders 0 1 0 Output

3 R 0 2 6 0 1 R 1 2 3 1 0

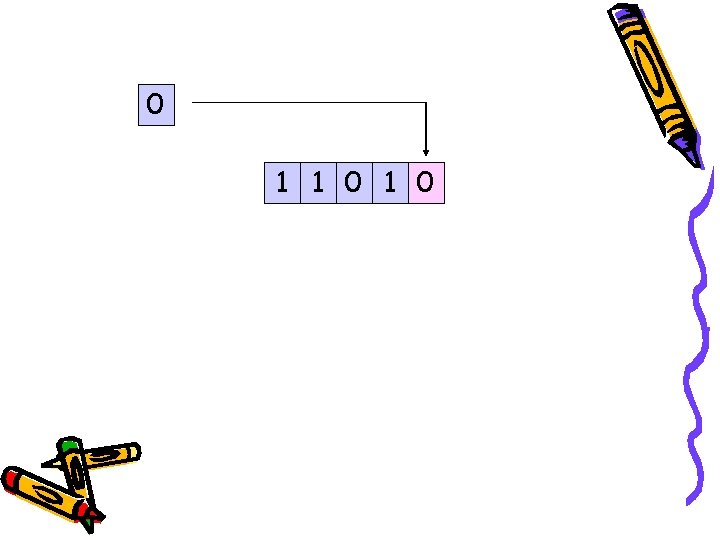
0 R 1 2 1 1 1 0 1

1 0 1 0 1 1 0 1

0 1 1 0