Stack Array Elements are stored in continuous contiguous

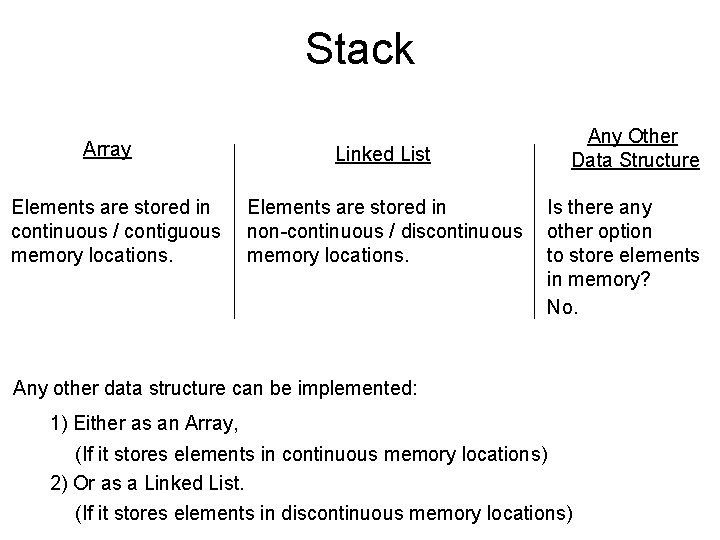
Stack Array Elements are stored in continuous / contiguous memory locations. Any Other Data Structure Linked List Elements are stored in non-continuous / discontinuous memory locations. Is there any other option to store elements in memory? No. Any other data structure can be implemented: 1) Either as an Array, (If it stores elements in continuous memory locations) 2) Or as a Linked List. (If it stores elements in discontinuous memory locations)

Stack Examples Stack of Books Box of Tennis Balls (Closed at 1 end) Stack of Plates Stack of Clothes. Trains in a railway yard. Goods in a cargo. Type: Stack of Rings / Discs LIFO / FILO Stack of Chairs

Stack • Stack: –Collection of, • Homogeneous data elements where, • Insertion and deletion take place, –At one end only. –Also called, • LIFO structure. –Last In First Out. • FILO structure. –First In Last Out. –Stack can be implemented, • Either as an Array, –Stores the elements in continuous memory locations and, –Has all advantages/disadvantages of array. • Or as a Linked List. –Stores the elements in discontinuous memory locations and, –Has all advantages/disadvantages of linked list.

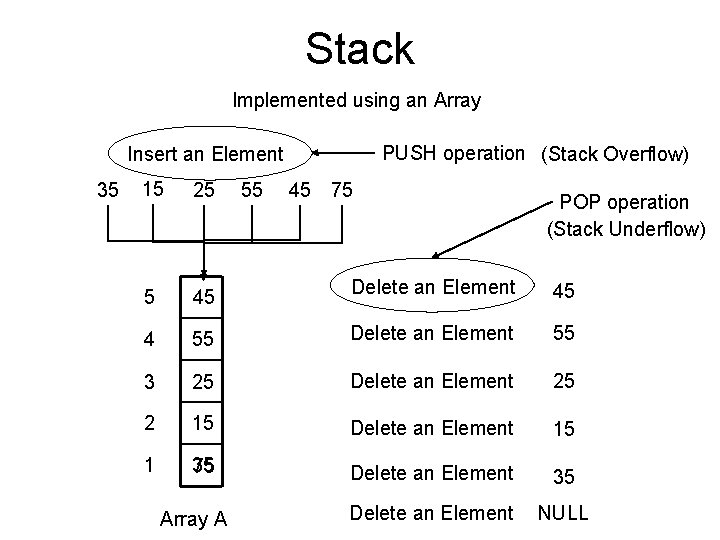
Stack Implemented using an Array PUSH operation (Stack Overflow) Insert an Element 35 15 25 5 45 Delete an Element 45 4 55 Delete an Element 55 3 25 Delete an Element 25 2 15 Delete an Element 15 1 35 75 Delete an Element 35 Delete an Element NULL Array A 55 45 75 POP operation (Stack Underflow)

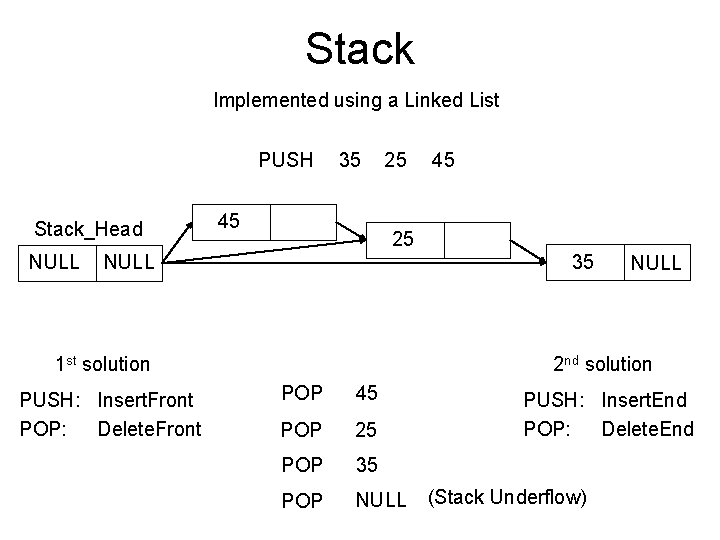
Stack Implemented using a Linked List PUSH Stack_Head NULL 35 45 25 25 35 NULL 1 st solution PUSH: Insert. Front POP: Delete. Front 45 NULL 2 nd solution POP 45 POP 25 POP 35 POP NULL PUSH: Insert. End POP: Delete. End (Stack Underflow)

Stack • Stack: –Insertion operation in a Stack is called: • PUSH –When PUSH is not possible, situation is called: » Stack Overflow –Deletion operation in a Stack is called: • POP –When POP is not possible, situation is called: » Stack Underflow

Stack using Array PUSH an element 25 15 35 65 55 Array A 5 55 4 65 3 35 2 15 1 25 POP POP 55 65 35 15 Is this logic efficient? No Inefficient for a bigger array.

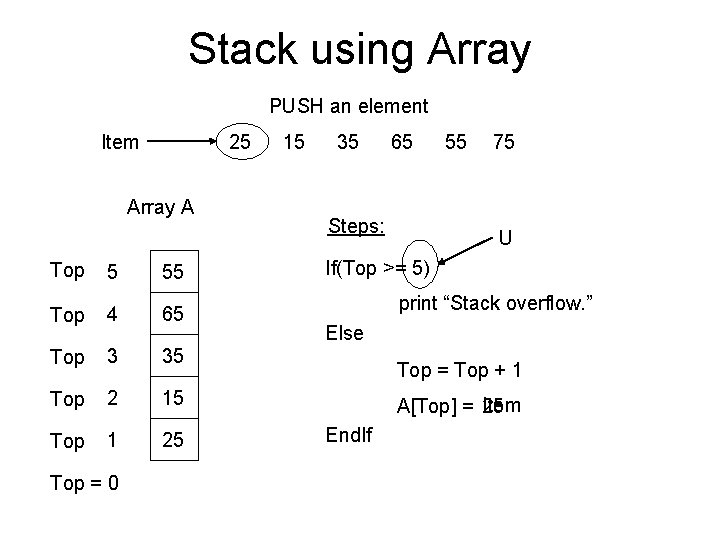
Stack using Array PUSH an element Item 25 Array A Top 5 55 Top 4 65 Top 3 35 Top 2 15 Top 1 25 Top = 0 15 35 65 Steps: 55 75 U If(Top >= 5) print “Stack overflow. ” Else Top = Top + 1 Item A[Top] = 25 End. If

Stack using Array POP POP POP 55 Array A 65 35 15 25 NULL Steps: Item = Null L If(Top < 1) Top 5 55 Top 4 65 Top 3 35 Top 2 15 Item = A[Top] // 5565 31 5525 A[Top] = Null Top 1 25 Top = Top - 1 Top = 0 print “Stack underflow. ” Else End. If Return(Item)

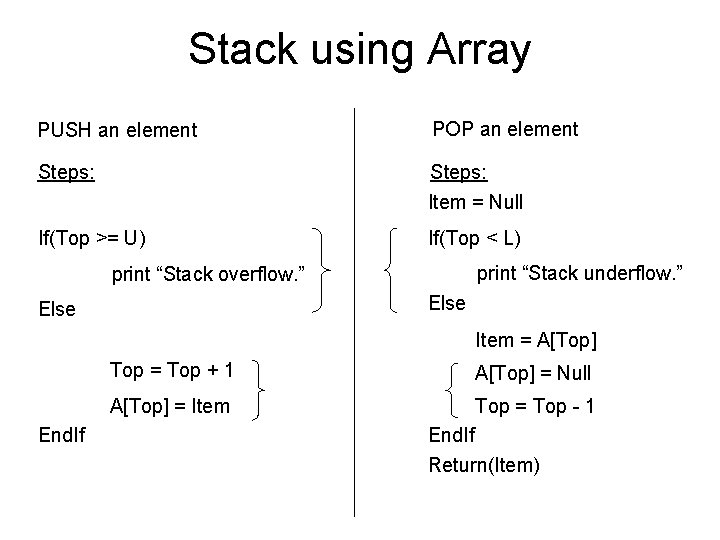
Stack using Array PUSH an element POP an element Steps: Item = Null If(Top >= U) If(Top < L) print “Stack underflow. ” print “Stack overflow. ” Else Item = A[Top] End. If Top = Top + 1 A[Top] = Null A[Top] = Item Top = Top - 1 End. If Return(Item)

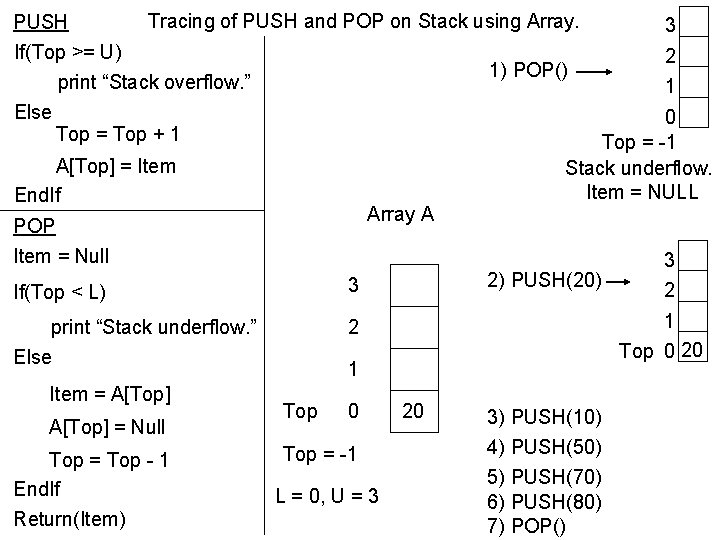
Tracing of PUSH and POP on Stack using Array. PUSH If(Top >= U) 1) POP() print “Stack overflow. ” Else Top = Top + 1 If(Top < L) 3 print “Stack underflow. ” Else 2 Top = Top - 1 End. If Return(Item) 1 Array A POP Item = Null A[Top] = Null 2 0 Top = -1 Stack underflow. Item = NULL A[Top] = Item End. If Item = A[Top] 3 2) PUSH(20) 0 Top = -1 L = 0, U = 3 2 1 Top 0 20 1 Top 3 20 3) PUSH(10) 4) PUSH(50) 5) PUSH(70) 6) PUSH(80) 7) POP()

Stack using Array • Algorithm: –Push_Array • Input: –Top: Pointer to the Top of Stack. –Item: Data to be pushed onto the Stack. • Output: –Stack with newly pushed item at Top if successful, message otherwise. • Data Structure: –Stack implemented using Array A[L. . . U] with TOP as the pointer.

Algorithm: Push_Array Steps: If(Top >= U) print “Stack overflow. ” Else Top = Top + 1 A[Top] = Item End. If Stop

Stack using Array • Algorithm: –Pop_Array • Input: –Top: Pointer to the Top of Stack. • Output: –Item: Data removed (popped) from Top of Stack if successful, NULL and message otherwise. • Data Structure: –Stack implemented using Array A[L. . . U] with Top as the pointer.

Steps: Algorithm: Pop_Array Item = Null If(Top < L) print “Stack underflow. ” Else Item = A[Top] = Null Top = Top - 1 End. If Return(Item) Stop

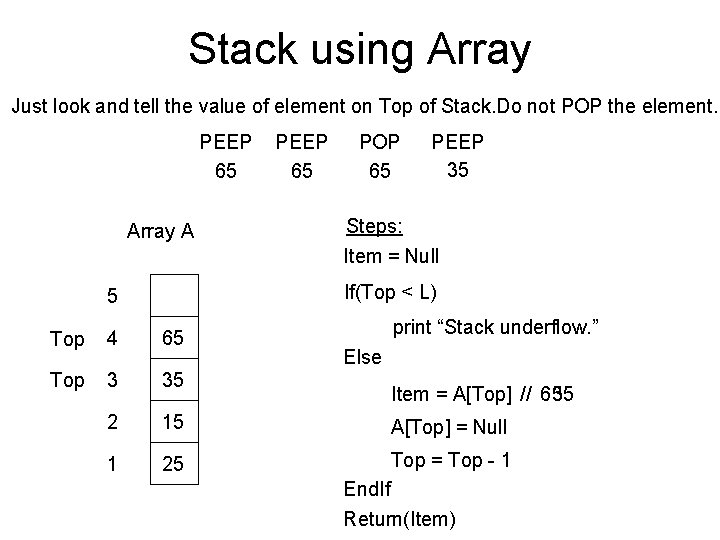
Stack using Array Just look and tell the value of element on Top of Stack. Do not POP the element. PEEP 65 Array A PEEP 65 POP 65 PEEP 35 Steps: Item = Null If(Top < L) 5 print “Stack underflow. ” Top 4 65 Top 3 35 2 15 A[Top] = Null 1 25 Top = Top - 1 Else Item = A[Top] // 65 35 End. If Return(Item)

Stack using Array • Algorithm: –Peep_Array • Input: –Top: Pointer to the Top of Stack. • Output: –Item: Data returned (not deleted) from Top of Stack if successful, message otherwise. • Data Structure: –Stack implemented using Array A[L. . . U] with Top as the pointer.

Steps: Algorithm: Peep_Array Item = Null If(Top < L) print “Stack underflow. ” Else Item = A[Top] End. If Return(Item) Stop

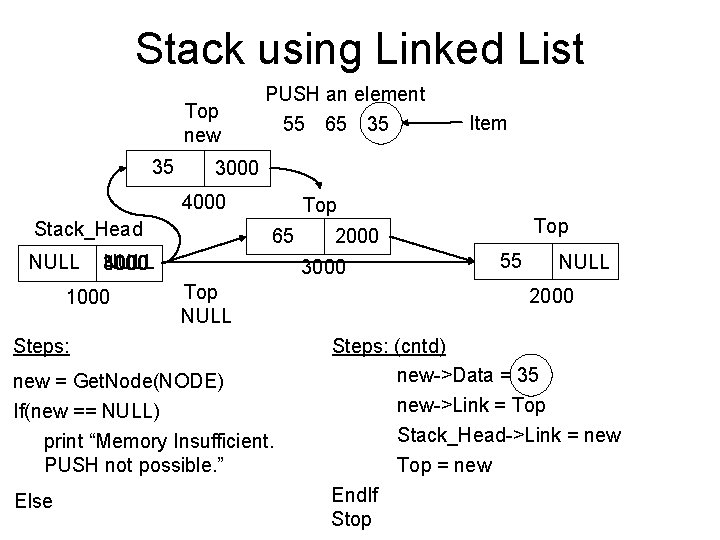
Stack using Linked List Top new 35 PUSH an element 55 65 35 3000 4000 Stack_Head NULL Top 65 NULL 3000 4000 1000 Top NULL new = Get. Node(NODE) If(new == NULL) print “Memory Insufficient. PUSH not possible. ” Top 2000 3000 Steps: Else Item 55 NULL 2000 Steps: (cntd) new->Data = 35 new->Link = Top Stack_Head->Link = new Top = new End. If Stop

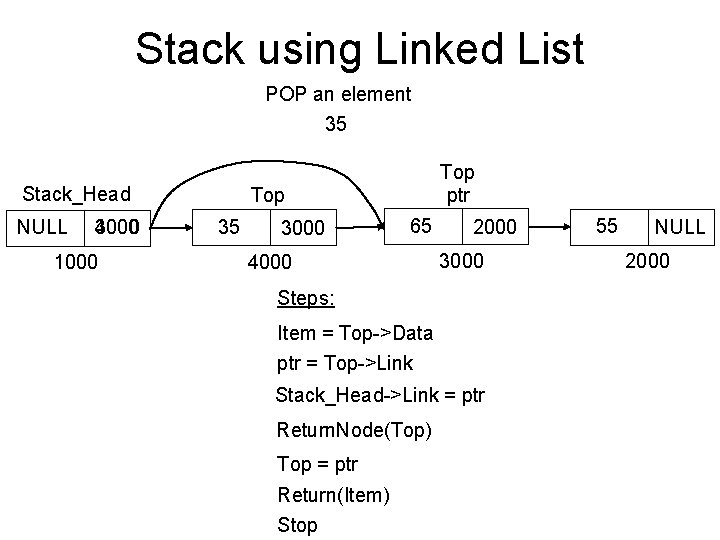
Stack using Linked List POP an element 35 Stack_Head NULL 3000 4000 1000 Top ptr Top 35 3000 65 4000 2000 3000 Steps: Item = Top->Data ptr = Top->Link Stack_Head->Link = ptr Return. Node(Top) Top = ptr Return(Item) Stop 55 NULL 2000

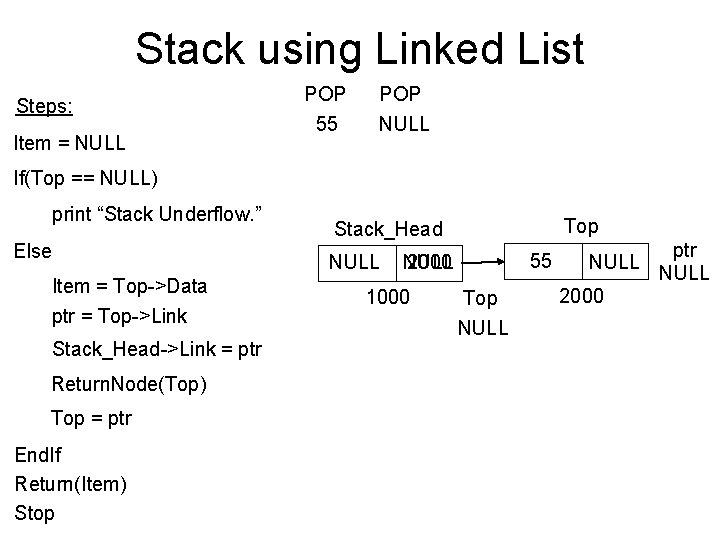
Stack using Linked List Steps: Item = NULL POP 55 POP NULL If(Top == NULL) print “Stack Underflow. ” Else Item = Top->Data ptr = Top->Link Stack_Head->Link = ptr Return. Node(Top) Top = ptr End. If Return(Item) Stop Top Stack_Head NULL 55 NULL 2000 1000 Top NULL 2000 ptr NULL

Stack using Linked List PUSH an element Steps: POP an element Steps: Trace the following steps on an new = Get. Node(NODE) Item = NULL empty Stack If(new == NULL) If(Top == NULL) implemented print “Memory Insufficient. print “Stack Underflow. ” using a Linked PUSH not possible. ” List: Else 1) PUSH(20) Item = Top->Data new->Data = Item 2) POP() ptr = Top->Link 3) PUSH(10) new->Link = Top Stack_Head->Link = ptr 4) PUSH(30) Stack_Head->Link = new 5) POP() Return. Node(Top) 6) POP() Top = new Top = ptr 7) POP() End. If Convert into Return(Item) Stop a program. Stop

Stack using Linked List • Algorithm: –Push_LL • Input: –Stack_Head: Pointer to the starting of linked list. –Top: Pointer to the Top of Stack. –Item: Data to be pushed onto the Stack. • Output: –Stack with newly pushed item at Top if successful, message otherwise. • Data Structure: –Stack implemented using Single Linked List with, • Stack_Head as pointer to the starting of linked list and, • Top as the pointer to the Top of Stack.

Algorithm: Push_LL Steps: new = Get. Node(NODE) If(new == NULL) print “Memory Insufficient. Push not possible. ” Else new->Data = Item new->Link = Top Stack_Head->Link = new Top = new End. If Stop

Stack using Linked List • Algorithm: –Pop_LL • Input: –Stack_Head: Pointer to the starting of linked list. –Top: Pointer to the Top of Stack. • Output: –Item: Element removed (popped) from the Top of Stack if successful, message otherwise. • Data Structure: –Stack implemented using Single Linked List with, • Stack_Head as pointer to the starting of linked list and, • Top as the pointer to the Top of Stack.

Algorithm: Pop_LL Steps: Item = NULL If(Top == NULL) print “Stack Underflow. ” Else Item = Top->Data ptr = Top->Link Stack_Head->Link = ptr Return. Node(Top) Top = ptr End. If Return(Item) Stop

Applications of Stack • Uses of Stack: –Main uses of Stack are: • Evaluation of Arithmetic Expression –Example: » ( A + B ) * C or ( 1 + 2 ) * 3 • Execute recursive function calls / Recursion.

Applications of Stack Evaluation of Arithmetic Expression using a Stack How can it be solved by a computer? E= A+B 2+3 [A = 2, B = 3] Scanning the input once from Left to Right and doing appropriate processing. E= A+B-C 1+2 -3 [A = 1, B = 2, C = 3] Scanning the input once from Left to Right and doing appropriate processing. E= A+B*C 1+2*3 [A = 1, B = 2, C = 3] Requires scanning of the input multiple times from Left to Right. E= A–((B+C)*D) 1–((2+3)*4) [A = 1, B = 2, C = 3, D = 4] Requires scanning of the input several times from Left to Right.

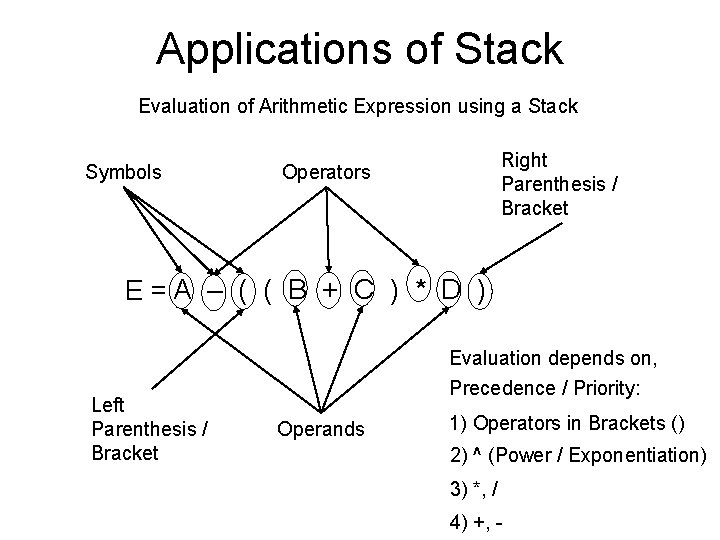
Applications of Stack Evaluation of Arithmetic Expression using a Stack Symbols Right Parenthesis / Bracket Operators E =A – ( ( B + C ) * D ) Left Parenthesis / Bracket Evaluation depends on, Precedence / Priority: Operands 1) Operators in Brackets () 2) ^ (Power / Exponentiation) 3) *, / 4) +, -

Applications of Stack • Evaluation of Arithmetic Expression using a Stack: –Process consist of 2 steps: • 1) Convert the given arithmetic expression into a special notation/representation using a Stack. –Algorithm would be required for this step. • 2) Evaluate (Find the value of) that special notation (obtained from step-1) again using a Stack. –Algorithm would be required for this step.

Evaluation of Arithmetic Expression using a Stack Step-1: Convert expression into special notation using a Stack. Input Expression: A + B Enclose / Put the input in Parentheses (if not already enclosed) So input Expression becomes: Infix Expression ( A + B ) Step Symbol 1 ( 2 A 3 + Stack T Output Expression T ( T A ( T ( + T 4 B ( + 5 ) - A AB AB+ Postfix Expression

Stack should be empty at the end of the conversion. Infix to Postfix expression never contains parentheses. Infix Expression: A * B + C Infix Expression enclosed in parentheses: ( A * B + C ) Step Symbol Stack 1 2 A T * ( A ( T T 4 B ( * 5 + ( + 6 C 7 ) Output Expression T ( 3 T T T ( + A AB AB* AB *C +

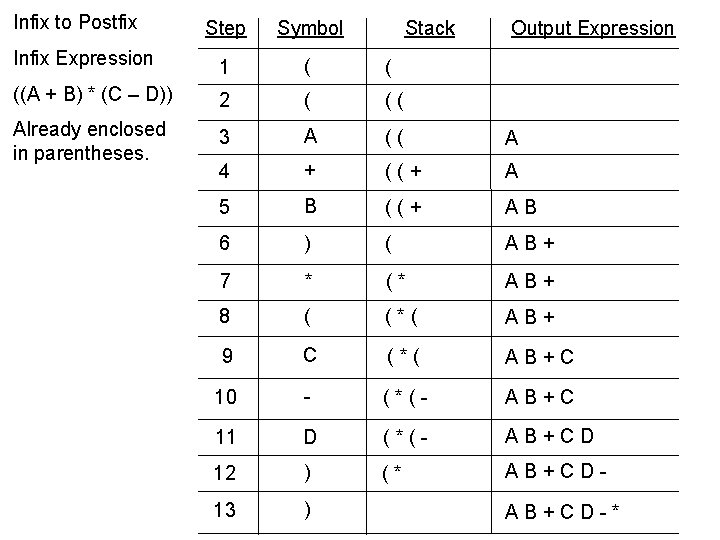
Infix to Postfix Step Symbol Stack Output Expression Infix Expression 1 ( ( ((A + B) * (C – D)) 2 ( (( Already enclosed in parentheses. 3 A (( A 4 + ((+ A 5 B ((+ AB 6 ) ( AB+ 7 * (* AB+ 8 ( (*( AB+ 9 C (*( AB+C 10 - (*(- AB+C 11 D (*(- AB+CD 12 ) (* AB+CD- 13 ) AB+CD-*

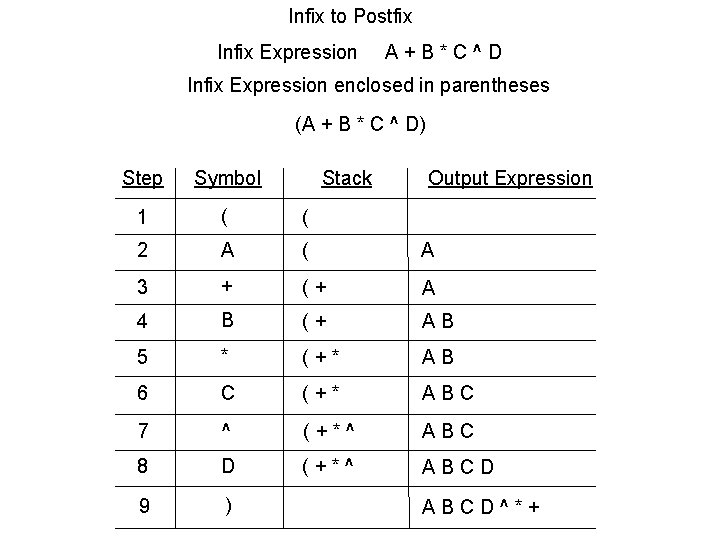
Infix to Postfix Infix Expression A+B*C^D Infix Expression enclosed in parentheses (A + B * C ^ D) Step Symbol Stack Output Expression 1 ( ( 2 A ( A 3 + (+ A 4 B (+ AB 5 * (+* AB 6 C (+* ABC 7 ^ (+*^ ABC 8 D (+*^ ABCD 9 ) ABCD^*+

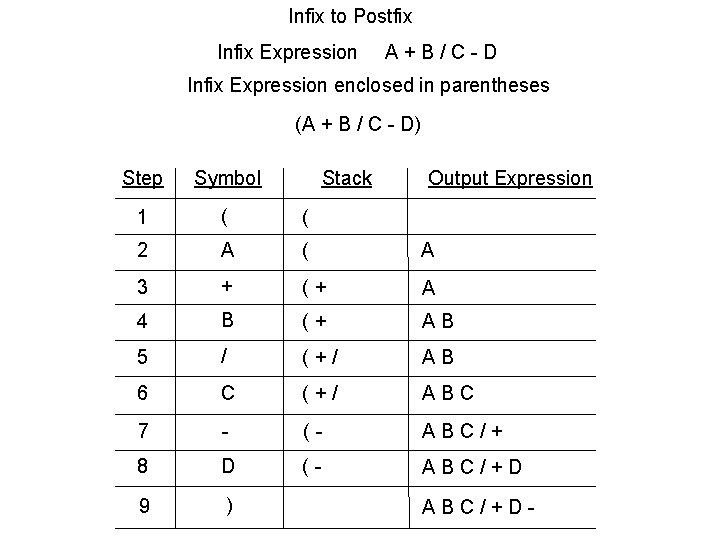
Infix to Postfix Infix Expression A+B/C-D Infix Expression enclosed in parentheses (A + B / C - D) Step Symbol Stack Output Expression 1 ( ( 2 A ( A 3 + (+ A 4 B (+ AB 5 / (+/ AB 6 C (+/ ABC 7 - (- ABC/+ 8 D (- ABC/+D 9 ) ABC/+D-

Infix to Postfix Convert the following arithmetic expressions from Infix to Postfix. (A+B)^C–(D*E)/F (A+((B^C)–D))*(E–(A/C)) A+(B*C)/D (A+B)*C A*B^C+D

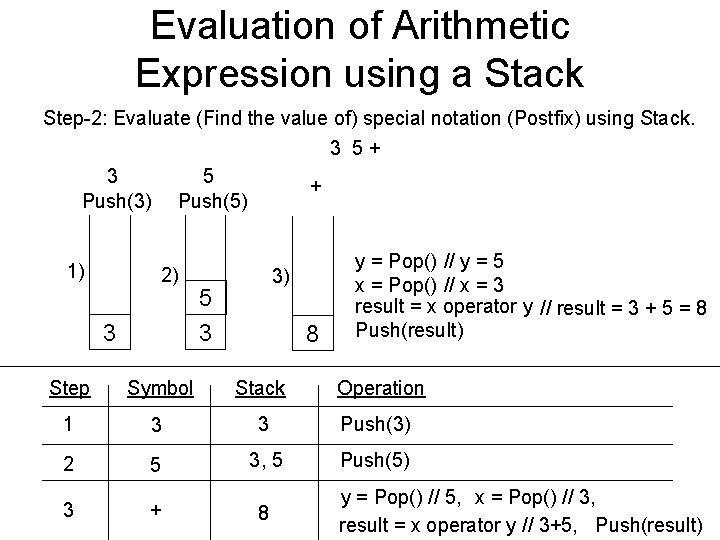
Evaluation of Arithmetic Expression using a Stack Step-2: Evaluate (Find the value of) special notation (Postfix) using Stack. Infix Expression: A + B Step-1 Postfix Expression: A B + Values: A = 3, B = 5 Postfix Expression: A B + 3 5+ 3 Push(3) 1) 5 Push(5) 2) 3) 3 Operands Operator + 5 3 35+ 8 y = Pop() // y = 5 x = Pop() // x = 3 result = x operator y // result = 3 + 5 = 8 Push(result)

Evaluation of Arithmetic Expression using a Stack Step-2: Evaluate (Find the value of) special notation (Postfix) using Stack. 3 5+ 3 Push(3) 1) 5 Push(5) 2) 3 + 3) 5 3 8 y = Pop() // y = 5 x = Pop() // x = 3 result = x operator y // result = 3 + 5 = 8 Push(result) Step Symbol Stack Operation 1 3 3 Push(3) 2 5 3, 5 Push(5) 3 + 8 y = Pop() // 5, x = Pop() // 3, result = x operator y // 3+5, Push(result)

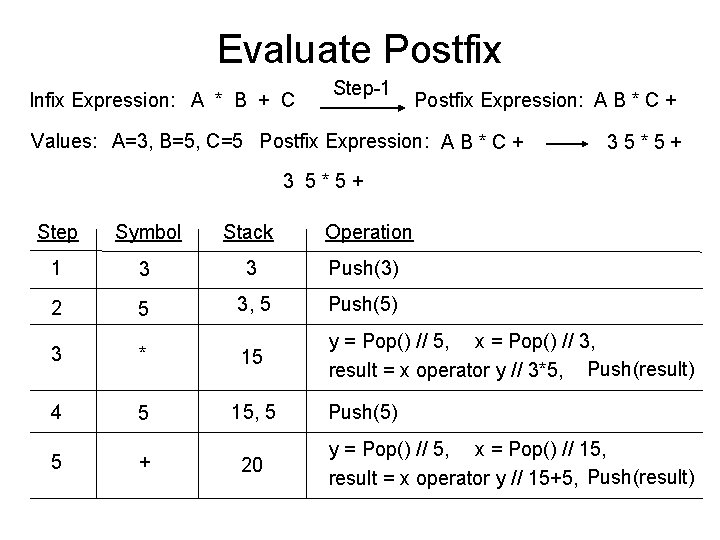
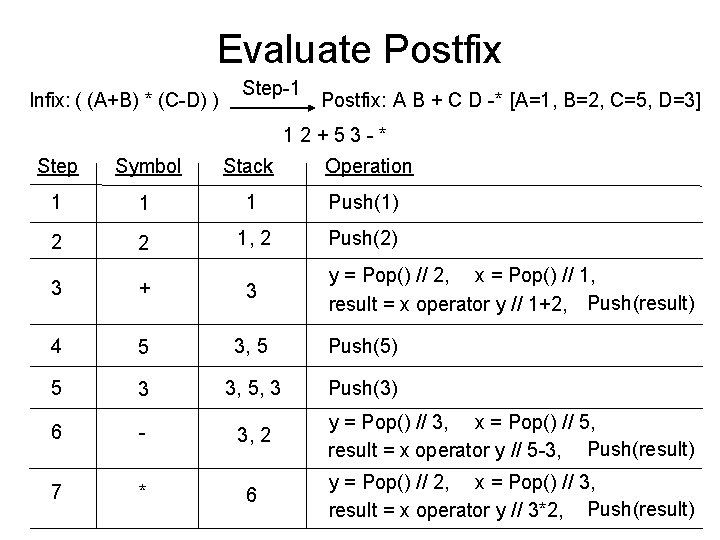
Evaluate Postfix Infix Expression: A * B + C Step-1 Postfix Expression: A B * C + Values: A=3, B=5, C=5 Postfix Expression: A B * C + 35*5+ 3 5*5+ Step Symbol Stack Operation 1 3 3 Push(3) 2 5 3, 5 Push(5) 3 * 15 y = Pop() // 5, x = Pop() // 3, result = x operator y // 3*5, Push(result) 4 5 15, 5 5 + 20 Push(5) y = Pop() // 5, x = Pop() // 15, result = x operator y // 15+5, Push(result)

Evaluate Postfix Infix: ( (A+B) * (C-D) ) Step-1 Postfix: A B + C D -* [A=1, B=2, C=5, D=3] 12+53 -* Step Symbol Stack Operation 1 1 1 Push(1) 2 2 1, 2 Push(2) 3 + 3 4 5 3, 5 Push(5) 5 3 3, 5, 3 Push(3) 6 - 3, 2 y = Pop() // 3, x = Pop() // 5, result = x operator y // 5 -3, Push(result) 7 * 6 y = Pop() // 2, x = Pop() // 3, result = x operator y // 3*2, Push(result) y = Pop() // 2, x = Pop() // 1, result = x operator y // 1+2, Push(result)

Evaluation of Arithmetic Expression using a Stack Exercise: Evaluate the following Arithmetic Expression using a Stack: (A*B)-(C/D) [ A = 1, B = 3, C = 8, D = 2 ] Steps: 1) Infix to Postfix AB*CD/- 2) Evaluate Postfix -1

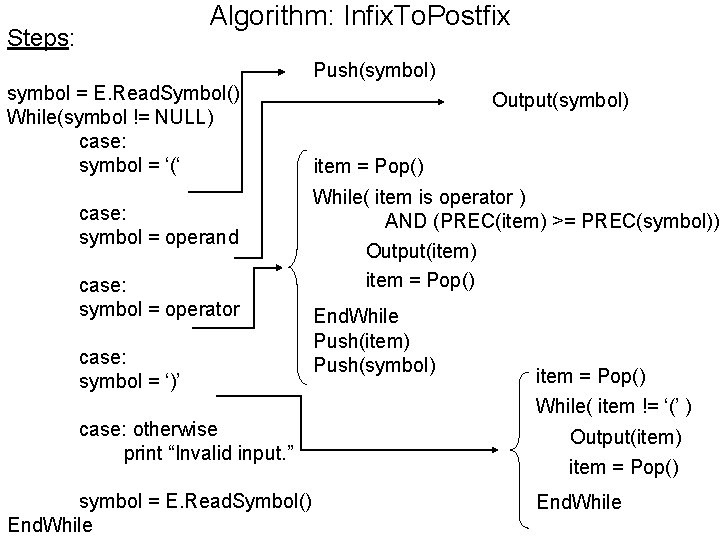
Algorithm: Infix. To. Postfix • Algorithm-Infix. To. Postfix: –Enclose the entire expression in parentheses (brackets) if not already enclosed. • Add ‘(‘ at the beginning and ‘)’ at the end of the expression. –Scan 1 symbol at a time from left to right and do the following things depending on the type of symbol scanned: • If symbol is ‘(‘: –Push it onto the stack. • If symbol is ‘Operand’: –Add/Append it to the Output Expression/Output String/Postfix Expression. • If symbol is ‘Operator’: –Pop all the operators one by one from TOP of stack which have, » The same or higher precedence than the symbol and go on, » Adding them to the Output String. –Then push the incoming operator onto the stack. • If symbol is ‘)’: –Pop all the operators one by one from TOP of stack and go on adding them to the Output String until, » ‘(‘ is encountered / obtained. –Remove that ‘(‘ from the Stack and do not do anything with ‘)’.

Algorithm: Infix. To. Postfix Steps: Push(symbol) symbol = E. Read. Symbol() While(symbol != NULL) case: symbol = ‘(‘ case: symbol = operand case: symbol = operator case: symbol = ‘)’ Output(symbol) item = Pop() While( item is operator ) AND (PREC(item) >= PREC(symbol)) Output(item) item = Pop() End. While Push(item) Push(symbol) item = Pop() While( item != ‘(’ ) case: otherwise print “Invalid input. ” symbol = E. Read. Symbol() End. While Output(item) item = Pop() End. While

Steps: Algorithm: Evaluate. Postfix symbol = E. Read. Symbol() While(symbol != NULL) case: symbol = operand Push(symbol) case: symbol = operator y = Pop() x = Pop() result = x symbol y Push(result) case: otherwise print “Invalid input. ” symbol = E. Read. Symbol() End. While value = Pop() Return(value) Stop