Stable Feature Selection Theory and Algorithms Presenter Yue

Stable Feature Selection: Theory and Algorithms Presenter: Yue Han Advisor: Lei Yu Ph. D. Dissertation 4/26/2012 1

Outline �Introduction and Motivation �Background and Related Work �Major Contributions �Publications �Theoretical Framework for Stable Feature Selection �Empirical Framework : Margin Based Instance Weighting �Empirical Study Ø Ø Ø General Experimental Setup Experiments on Synthetic Data Experiments on Real-World Data �Conclusion and Future Work 2

Feature Selection Applications Gene Selection Pixel Selection Word Selection Sports Travel Politics Tech Artist Life Science Internet. Business Health Elections 3

Feature Selection from High-dimensional Data High-Dimensional Data Feature Selection Algorithms Low. Dimensional Data Learning Models Knowledge Discovery on High-dimensional Data p: # of features n: # of samples High-dimensional data: p >> n Curse of Dimensionality: • Effects on distance functions • In optimization and learning • In Bayesian statistics Feature Selection: ØAlleviating the effect of the curse of dimensionality. ØEnhancing generalization capability. ØSpeeding up learning process. ØImproving model interpretability. 4
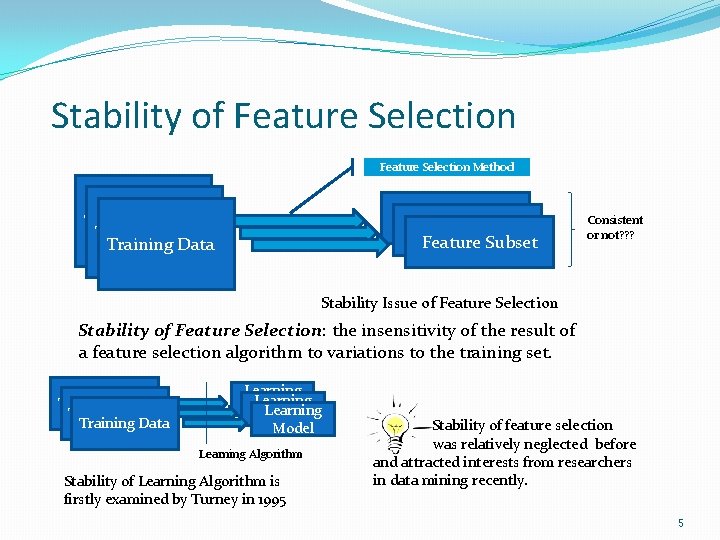
Stability of Feature Selection Method Feature Subset Training Data Consistent or not? ? ? Stability Issue of Feature Selection Stability of Feature Selection: the insensitivity of the result of a feature selection algorithm to variations to the training set. Training Data Learning Model Learning Algorithm Stability of Learning Algorithm is firstly examined by Turney in 1995 Stability of feature selection was relatively neglected before and attracted interests from researchers in data mining recently. 5

Motivation for Stable Feature Selection Sample Space D Training Data D 1 Training Data D 2 Given Unlimited Sample Size: Feature selection results from D 1 and D 2 are the same Given Limited Sample Size: (n<<p for high dimensional data) Feature selection results from D 1 and D 2 are different Biologists cares about: üPrediction accuracy & Consistency of feature subsets; üConfidence for biological validation ; üBiomarkers to explain the observed phenomena. 6

Outline �Introduction and Motivation �Background and Related Work �Major Contributions �Publications �Theoretical Framework for Stable Feature Selection �Empirical Framework : Margin Based Instance Weighting �Empirical Study Ø Ø Ø General Experimental Setup Experiments on Synthetic Data Experiments on Real-World Data �Conclusion and Future Work 7
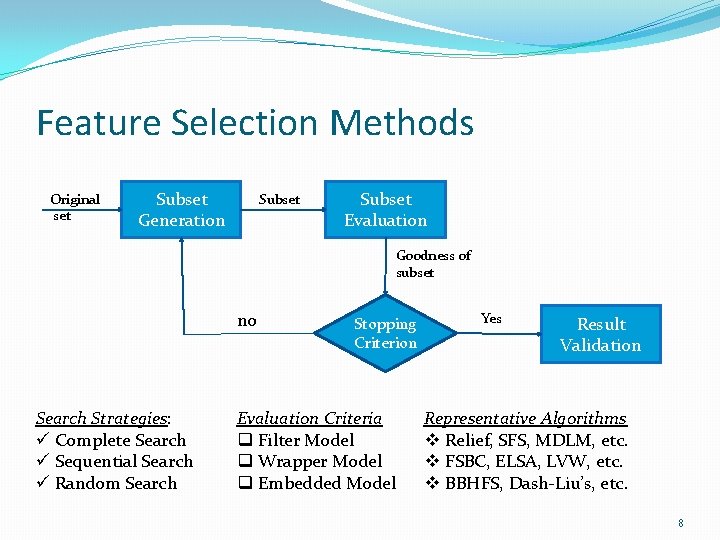
Feature Selection Methods Original set Subset Generation Subset Evaluation Goodness of subset no Search Strategies: ü Complete Search ü Sequential Search ü Random Search Stopping Criterion Evaluation Criteria q Filter Model q Wrapper Model q Embedded Model Yes Result Validation Representative Algorithms v Relief, SFS, MDLM, etc. v FSBC, ELSA, LVW, etc. v BBHFS, Dash-Liu’s, etc. 8

Stable Feature Selection Comparison of Feature Selection Algorithms w. r. t. Stability (Davis et al. Bioinformatics, vol. 22, 2006; Kalousis et al. KAIS, vol. 12, 2007) üQuantify the stability in terms of consistency on subset or weight; üAlgorithms varies on stability and equally well for classification; üChoose the best with both stability and accuracy. Bagging-based Ensemble Feature Selection (Saeys et al. ECML 07) üDifferent bootstrapped samples of the same training set; üApply a conventional feature selection algorithm; üAggregates the feature selection results. Group-based Stable Feature Selection (Yu et al. KDD 08; Loscalzo et al. KDD 09) üExplore the intrinsic feature correlations; üIdentify groups of correlated features; üSelect relevant feature groups. 9

Margin based Feature Selection Sample Margin: how much can an instance travel before it hits the decision boundary Hypothesis Margin: how much can the hypothesis travel before it hits an instance (Distance between the hypothesis and the opposite hypothesis of an instance) Representative Algorithms based on HM: Relief-F, G-flip, Simba, etc. margin is used for feature weighting or feature selection (totally different use in our study) 10

Outline �Introduction and Motivation �Background and Related Work �Major Contributions �Publications �Theoretical Framework for Stable Feature Selection �Empirical Framework : Margin Based Instance Weighting �Empirical Study Ø Ø Ø General Experimental Setup Experiments on Synthetic Data Experiments on Real-World Data �Conclusion and Future Work 11

Publications � Yue Han and Lei Yu. Margin Based Sample Weighting for Stable Feature Selection. In Proceedings of the 11 th International Conference on Web-Age Information Management (WAIM 2010), pages 680 -691, Jiuzhaigou, China, July 15 -17, 2010. � Yue Han and Lei Yu. A Variance Reduction Framework for Stable Feature Selection. In Proceedings of the 10 th IEEE International Conference on Data Mining (ICDM 2010), pages 205 -215, Sydney, Australia, December 14 -17, 2010. � Lei Yu, Yue Han and Michael E. Berens. Stable Gene Selection from Microarray Data via Sample Weighting. IEEE/ACM Transactions on Computational Biology and Bioinformatics (TCBB), pages 262 -272, vol. 9 no. 1, 2012. � Yue Han and Lei Yu. A Variance Reduction Framework for Stable Feature Selection. Statistical Analysis and Data Mining(SADM), Accepted, 2012. 12

Outline �Introduction and Motivation �Background and Related Work �Major Contributions �Publications �Theoretical Framework for Stable Feature Selection �Empirical Framework : Margin Based Instance Weighting �Empirical Study Ø Ø Ø General Experimental Setup Experiments on Synthetic Data Experiments on Real-World Data �Conclusion and Future Work 13

Bias-variance Decomposition of Feature Selection Error Training Data: D Data Space: FS Result: r(D) True FS Result: r* Error: Bias: Variance: Bias-Variance Decomposition of Feature Selection Error: o. Relationship between accuracy(opposite of loss)&stability(opposite of variance); o Suggests a better trade-off between the bias and variance of feature selection. 14

Bias, Variance and Error of Monte Carlo Estimator Feature Selection (Weighting) Monte Carlo Estimator Relevance Score: Monte Carlo Estimator: Error: Bias: Variance: Impact Factor: feature selection algorithm and sample size Increasing • Impractical Sample size • Costly 15

Variance Reduction via Sample Weighting Probability density function Importance Sampling A good importance sampling function h(x) Importance Sampling Instance Weighting • More instances draw from important regions • Less instances draw from other regions • Increase weights for instances from important regions • Decrease weights for instances from other regions 16

Outline �Introduction and Motivation �Background and Related Work �Major Contributions �Publications �Theoretical Framework for Stable Feature Selection �Empirical Framework : Margin Based Instance Weighting �Empirical Study Ø General Experimental Setup Ø Experiments on Synthetic Data Ø Experiments on Real-World Data �Conclusion and Future Work 17
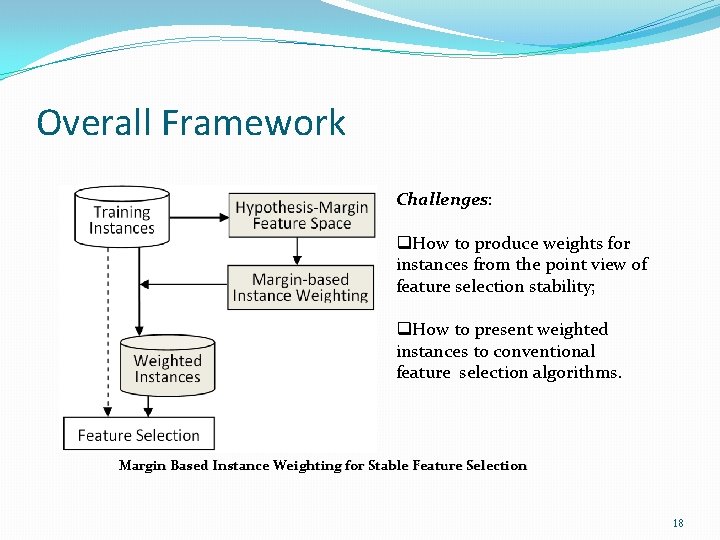
Overall Framework Challenges: q. How to produce weights for instances from the point view of feature selection stability; q. How to present weighted instances to conventional feature selection algorithms. Margin Based Instance Weighting for Stable Feature Selection 18
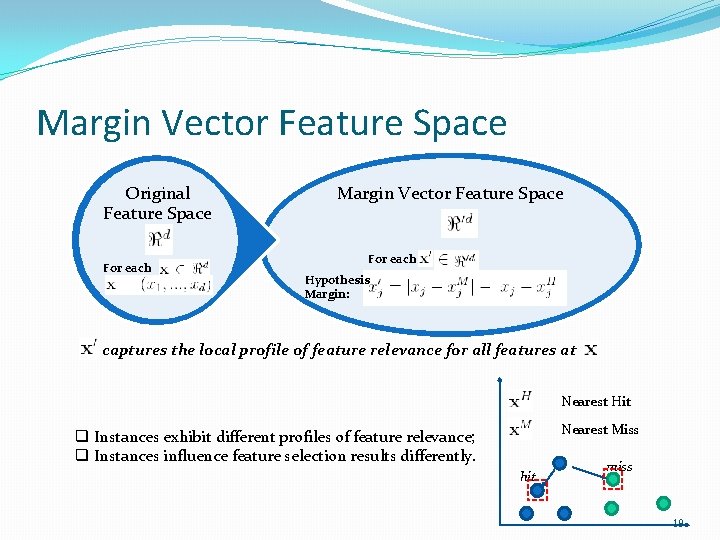
Margin Vector Feature Space Original Feature Space For each Margin Vector Feature Space For each Hypothesis Margin: captures the local profile of feature relevance for all features at Nearest Hit Nearest Miss q Instances exhibit different profiles of feature relevance; q Instances influence feature selection results differently. hit miss 19
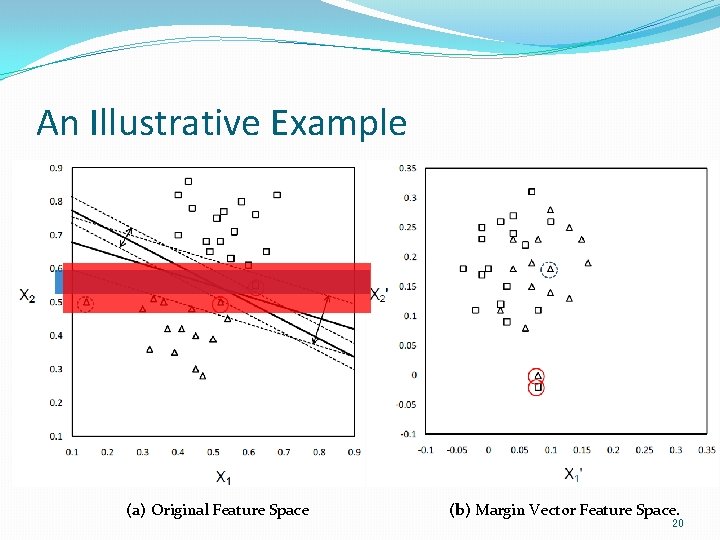
An Illustrative Example (a) Original Feature Space (b) Margin Vector Feature Space. 20

Extension for Hypothesis Margin of 1 NN q To reduce the effect of noise or outliers Hypothesis Margin of k. NN(k>1) Hypothesis Margin of weighted k. NN(k>1) 21
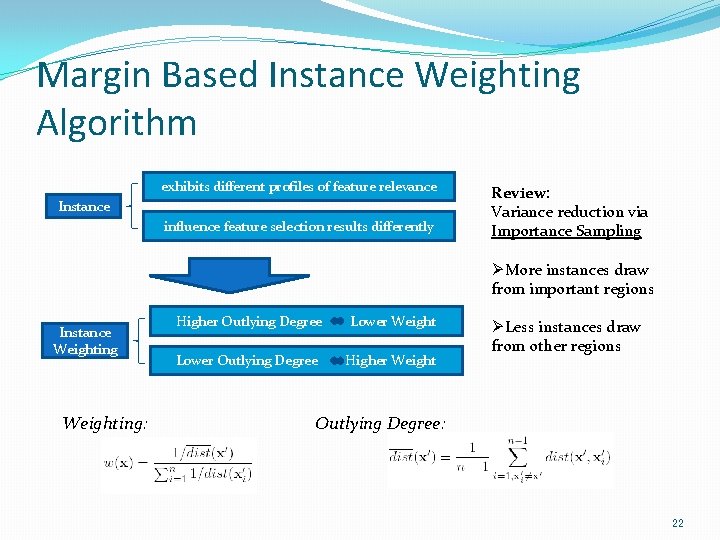
Margin Based Instance Weighting Algorithm exhibits different profiles of feature relevance Instance influence feature selection results differently Review: Variance reduction via Importance Sampling ØMore instances draw from important regions Instance Weighting: Higher Outlying Degree Lower Weight Lower Outlying Degree Higher Weight ØLess instances draw from other regions Outlying Degree: 22

Iterative Margin Based Instance Weighting Assumption: Instances are equally important in original feature space Original Weighted Feature Space Margin Vector Feature Space Instance Weight Updated Instance Weight Final Instance Weight v The iterative procedure always Converges fast; v There exists little difference in terms of learned weights; v Overall a stable procedure. 23

Algorithm Illustration Time Complexity Analysis: o Dominated by Instance Weighting: o Efficient for High-dimensional Data with small sample size (n<<d) 24

Outline �Introduction and Motivation �Background and Related Work �Major Contributions �Publications �Theoretical Framework for Stable Feature Selection �Empirical Framework : Margin Based Instance Weighting �Empirical Study Ø Ø Ø General Experimental Setup Experiments on Synthetic Data Experiments on Real-World Data �Conclusion and Future Work 25

Objective of Empirical Study v to demonstrate the bias-variance decomposition in theoretical framework; v to verify the effectiveness of the proposed instance weighting framework on variance reduction; v to study the impacts of variance reduction on the stability and predictive performance of the selected subsets. Feature Selection Method Training Data Feature Subset Consistent or not? ? ? Stability of Feature Selection 26

Algorithms in Comparison SVM-RFE Baseline Algorithm • Recursively eliminate 10 percent of training features each iteration • Linear kernel and default C parameter IW SVM-RFE Instance Weighting SVM-RFE • Instance weight affects error penalty and thus the choice of hyperplane En SVM-RFE Ensemble SVM-RFE • 20 bootstrapped training set • Aggregate different rankings into a final consensus ranking Relief-F Baseline Algorithm • Hypothesis Margin (produce feature weights) • Simply aggregate margin based on KNN along each feature dimension IW Relief-F Instance Weighting Relief-F • Instance weight affects the aggregated feature weight En Relief-F Ensemble Relief-F • 20 bootstrapped training set • Aggregate different rankings into a final consensus ranking 27

Predictive Accuracy Stability Measures, Predictive Accuracy Measures Feature Subset v. Jaccard Index; vn. POGR; v. SIMv; v. Kuncheva Index. Feature Ranking: v. Spearman Coefficient n. POGR: Kuncheva Index: Feature Weighting: v. Pearson Correlation Coefficient CV Accuracy: v. Prediction Accuracy base on Cross-validation AUC Accuracy: v the area under the receiver operating characteristic (ROC) Curve 28

Outline �Introduction and Motivation �Background and Related Work �Major Contributions �Publications �Theoretical Framework for Stable Feature Selection �Empirical Framework : Margin Based Instance Weighting �Empirical Study Ø Ø Ø General Experimental Setup Experiments on Synthetic Data Experiments on Real-World Data �Conclusion and Future Work 29

Experiments on Synthetic Data Generation: Feature Value: two multivariate normal distributions Covariance matrix is a 10*10 square matrix with elements 1 along the diagonal and 0. 8 off diagonal. 100 groups and 10 feature each 500 Training Data: 100 instances with 50 from and 50 from Leave-one-out Test Data: 5000 instances Method in Comparison: SVM-RFE: Recursively eliminate 10% features of previous iteration till 10 features remained. Measures: Variance, Bias, Error Subset Stability (Kuncheva Index) CV Accuracy (SVM) Class label: a weighted sum of all feature values with optimal feature weight vector 30
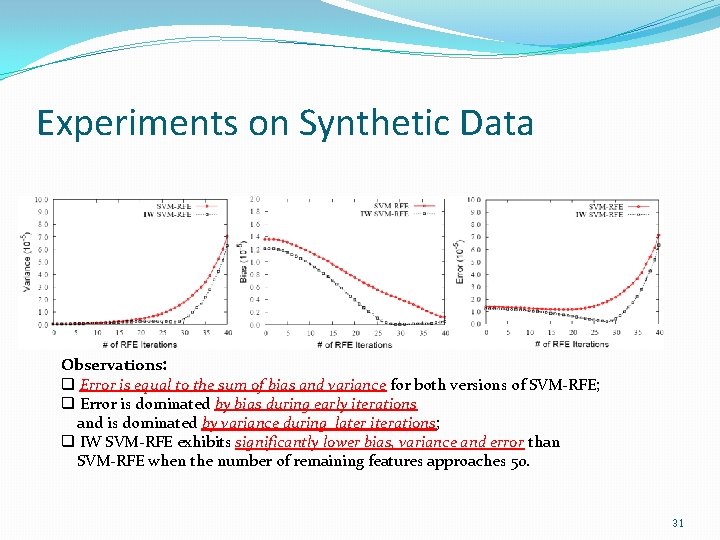
Experiments on Synthetic Data Observations: q Error is equal to the sum of bias and variance for both versions of SVM-RFE; q Error is dominated by bias during early iterations and is dominated by variance during later iterations; q IW SVM-RFE exhibits significantly lower bias, variance and error than SVM-RFE when the number of remaining features approaches 50. 31
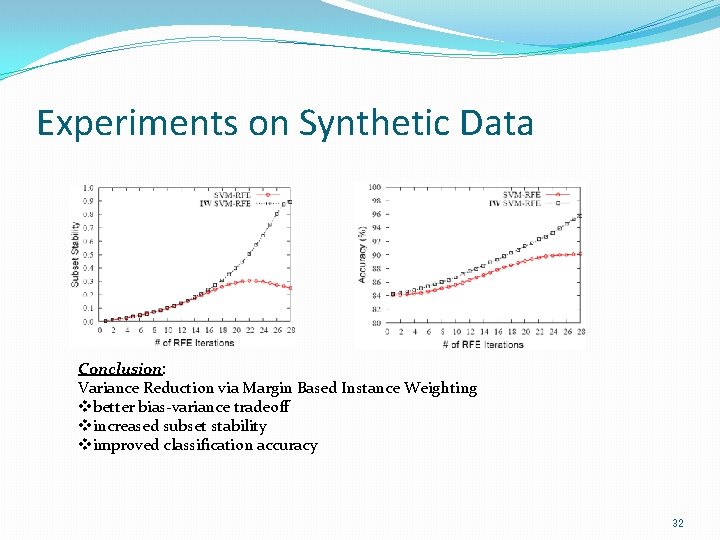
Experiments on Synthetic Data Conclusion: Variance Reduction via Margin Based Instance Weighting vbetter bias-variance tradeoff vincreased subset stability vimproved classification accuracy 32
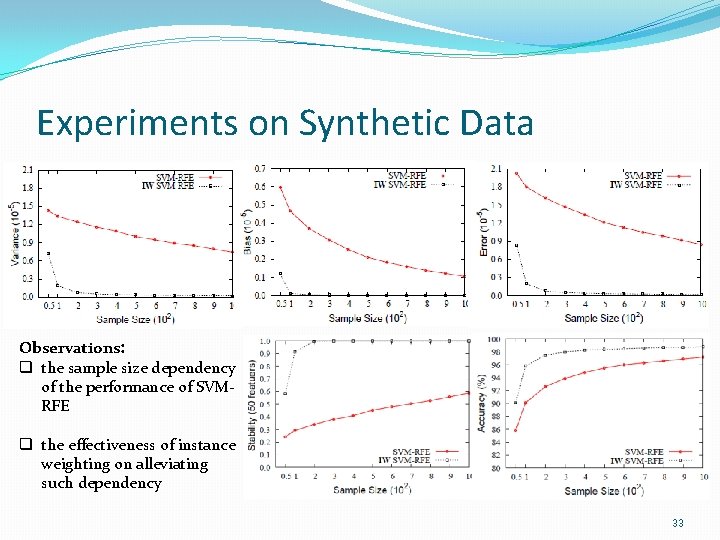
Experiments on Synthetic Data Observations: q the sample size dependency of the performance of SVMRFE q the effectiveness of instance weighting on alleviating such dependency 33

Outline �Introduction and Motivation �Background and Related Work �Major Contributions �Publications �Theoretical Framework for Stable Feature Selection �Empirical Framework : Margin Based Instance Weighting �Empirical Study Ø Ø Ø General Experimental Setup Experiments on Synthetic Data Experiments on Real-World Data �Conclusion and Future Work 34
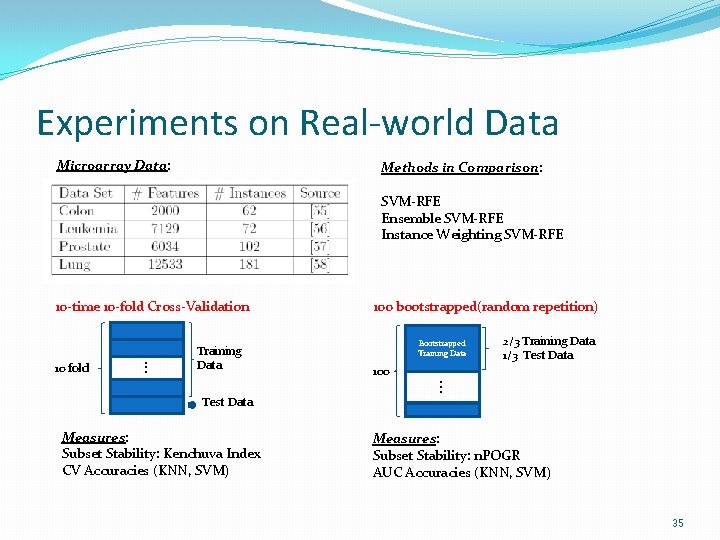
Experiments on Real-world Data Microarray Data: Methods in Comparison: SVM-RFE Ensemble SVM-RFE Instance Weighting SVM-RFE 10 -time 10 -fold Cross-Validation . . . 10 fold Training Data 100 bootstrapped(random repetition) Bootstrapped Training Data 2/3 Training Data 1/3 Test Data 100 . . . Test Data Measures: Subset Stability: Kenchuva Index CV Accuracies (KNN, SVM) Measures: Subset Stability: n. POGR AUC Accuracies (KNN, SVM) 35
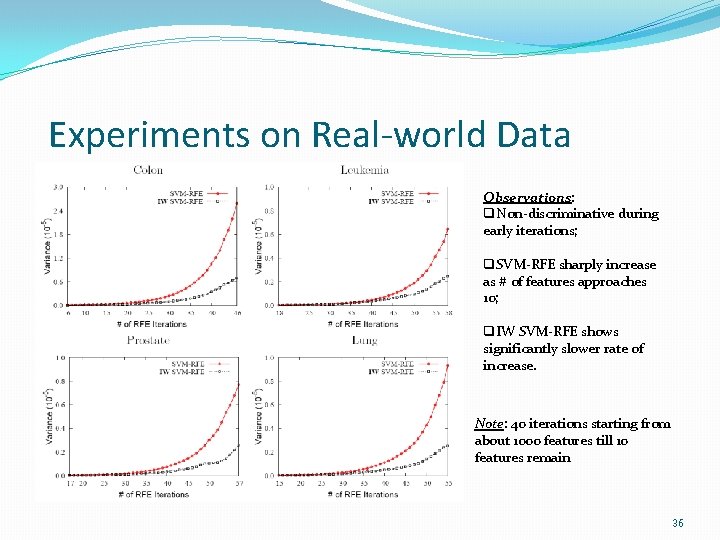
Experiments on Real-world Data Observations: q. Non-discriminative during early iterations; q. SVM-RFE sharply increase as # of features approaches 10; q. IW SVM-RFE shows significantly slower rate of increase. Note: 40 iterations starting from about 1000 features till 10 features remain 36
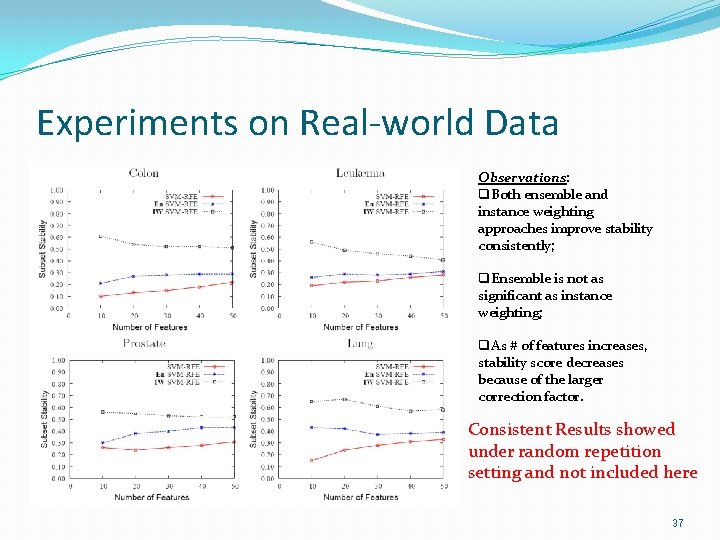
Experiments on Real-world Data Observations: q. Both ensemble and instance weighting approaches improve stability consistently; q. Ensemble is not as significant as instance weighting; q. As # of features increases, stability score decreases because of the larger correction factor. Consistent Results showed under random repetition setting and not included here 37
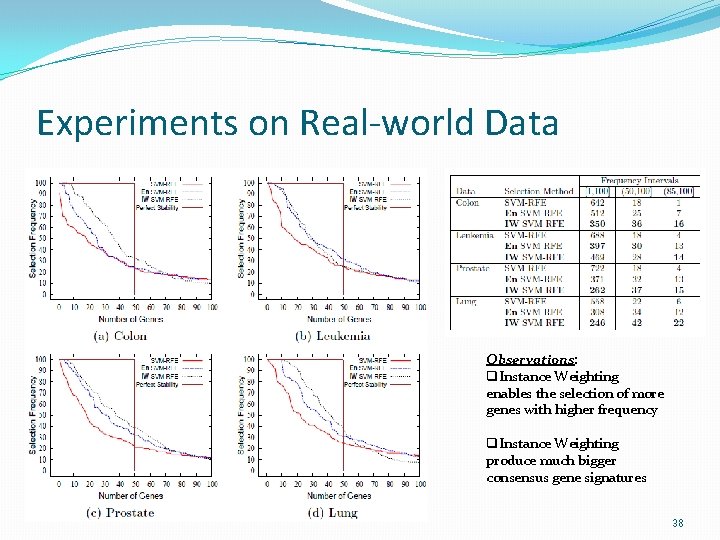
Experiments on Real-world Data Observations: q. Instance Weighting enables the selection of more genes with higher frequency q. Instance Weighting produce much bigger consensus gene signatures 38

Experiments on Real-world Data Conclusions: q. Improves stability of feature selection without sacrificing prediction accuracy; q. Performs much better than ensemble approach and more efficient; q. Leads to significantly increased stability with slight extra cost of time. Consistent Results showed under random repetition setting(also Relief. F) and results can be found in the dissertation but not included here for conciseness. 39

Outline �Introduction and Motivation �Background and Related Work �Major Contributions �Publications �Theoretical Framework for Stable Feature Selection �Empirical Framework : Margin Based Instance Weighting �Empirical Study Ø Ø Ø General Experimental Setup Experiments on Synthetic Data Experiments on Real-World Data �Conclusion and Future Work 40

Conclusion and Future Work Conclusion: v v v Theoretical Framework for Stable Feature Selection; Empirical Weighting Framework for Stable Feature Selection; Effective and Efficient Margin Based Instance Weighting Approaches; Extensive Study on Proposed Theoretical And Empirical Frameworks; Extensive Study on Proposed Weighting Approaches; Extensive Study on Sample Size Effect on Feature Selection Stability. Future Work: q Explore Other Weighting Approaches; q Study the Relationship Between Feature Selection and Classification w. r. t. Bias-Variance Properties. 41

Thank you and Questions? 42
- Slides: 42