Stability of liquid jets immersed in another liquid

Stability of liquid jets immersed in another liquid Part of the CONEX project „Emulsions with Nanoparticles for New Materials“ Univ. -Prof. Dr. Günter Brenn Ass. -Prof. Dr. Helfried Steiner Conex mid-term meeting, Oct. 28 to 30 2004, Warsaw Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 11

Contents • Introduction – break-up of submerged jets in emulsification • Description of jet dynamics • Linear stability analysis by Tomotika • Dispersion relation • Limitations to the applicability of the relation • Further work in the project Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 22

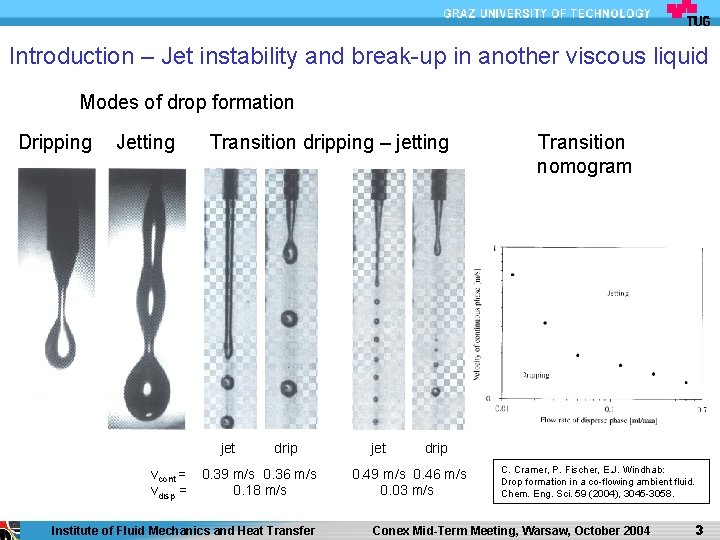
Introduction – Jet instability and break-up in another viscous liquid Modes of drop formation Dripping Jetting Transition dripping – jetting jet vcont = vdisp = drip 0. 39 m/s 0. 36 m/s 0. 18 m/s Institute of Fluid Mechanics and Heat Transfer jet Transition nomogram drip 0. 49 m/s 0. 46 m/s 0. 03 m/s C. Cramer, P. Fischer, E. J. Windhab: Drop formation in a co-flowing ambient fluid. Chem. Eng. Sci. 59 (2004), 3045 -3058. Conex Mid-Term Meeting, Warsaw, October 2004 33

Description of jet dynamics Basic equations of motion (u – r-velocity, w – z-velocity) Continuity r-momentum z-momentum For solution introduce the disturbance stream function to satisfy continuity Definition of stream function Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 44

Elimination of pressure and linearization Eliminating the pressure from the momentum equations yields with the differential operator Linearization: neglect products of velocities and their derivatives Final equation for the stream function reads Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 55

Solutions of the differential equation This differential equation is satisfied by functions 1 and 2 which are solutions of the two following equations We make the ansatz for wavelike solutions of the form where i = 1, 2 and obtain the amplitude functions where l 2=k 2+i / General solution of the linearised equation Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 66

Inner and outer solutions and boundary conditions Inner and outer solutions are specified from the general solution by excluding Bessel functions diverging for r→ 0 and for r→ , respectively inner where l´ 2 = k 2+i / ´, outer where l 2 = k 2+i / , Boundary conditions Velocities at the interface equal in the two sub-systems u´|r=a = u|r=a Continuity of tangential stress w´|r=a = w|r=a Jump of radial stress by surface tension where Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 77

Determinantal dispersion relation from boundary conditions The boundary conditions lead to the following dispersion relation with the functions F 1 through F 4 reading Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 88

Specialisation for low inertial effects Dispersion relation for neglected densities and ´ with the functions G 1, G 2, and G 4 reading Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 99

Graph of special dispersion relation for low inertia Dispersion relation for low inertia and ´/ =0. 91 (Taylor) Consequences • Wavelength for maximum wave growth is = 5. 53 2 a, since ka|opt = 0. 568. The dispersion relation is where • Drop size is Dd=2. 024 2 a. • Cut-off wavelength unchanged against the Rayleigh case of jet with ´=0 in a vacuum. S. Tomotika: On the instability of a cylindrical thread of a viscous liquid surrounded by another viscous fluid. Proc. R. Soc. London A 150 (1935), 322 -337. Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 1010

Comparison with Taylor’s experiment Flow situation: jet of lubricating oil in syrup Syrup Oil Syrup Dynamic viscosity ratio ´/ =0. 91 Calculation of the function (1 -x 2) (x) yields the maximum at ka = ka|opt = 0. 568 Measurements on photographs by Taylor yield a = 0. 272 mm, = 3. 452 mm → ka = 0. 495 Deviation of -13% → Tomotika claims satisfactory agreement Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 1111

Problems with applications of the Tomotika results • Undisturbed relative motion of the two fluids not accounted for • Most results derived from Tomotika in the literature without inertia Dispersion relation with relative motion of jet in an inviscid host medium C. Weber: Zum Zerfall eines Flüssigkeitsstrahles. ZAMM 11 (1931), 136 -154. • Inviscid host medium allows for top-hat velocity profiles • Analytical derivation of dispersion relation is therefore possible Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 1212

Remedy – dispersion relation from generalized approach Introduce into conservation the equations Continuity r-momentum z-momentum the correct disturbance approaches u = U + u´ and w = W + w´ with the quantities U and W of the undisturbed coaxial flow of a jet in its host medium, cancel terms of the undisturbed flow and neglect small quantities of higher order. → This leads again to a linearization of the momentum equations Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 1313

Conservation equations for the disturbances The disturbance approach with non-parallel flow (U≠ 0) yields Continuity r-momentum z-momentum Procedure for the calculation – further work in the project • Calculate U (r, z) and W(r, z) for the undisturbed flow in both fluids (possibly using a similarity approach ? ) • Eliminate the pressure disturbance from the above momentum equations • Introduce stream function of the disturbance in a wavelike form Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 1414

Summary, conclusions and further work • Instability of jets in another liquid is described by a determinantal dispersion relation • Maximum wave growth rate at ka ≈ 0. 57 for viscosity ratio close to one (Taylor’s experiment) • Limiting case of vanishing outer viscosity (Rayleigh, 1892) is contained in the solution • Cut-off wave number for instability remains unchanged against the Rayleigh (1879) case of an inviscid jet in a vacuum • Further work should lead to a description of jet instability with relative motion against the host medium. This will increase the value of the cut-off wave number Institute of Fluid Mechanics and Heat Transfer Conex Mid-Term Meeting, Warsaw, October 2004 1515