Stability Analysis characteristic equation CE lie in the

Stability Analysis characteristic equation (CE) lie in the LHP (left we can calculate the coefficient ai as follows an – 1= – pi half of complex plane). an – 2= pi pj, i j A system is BIBO stable if all poles or roots of an – 3= – pi pj pk, i j k Procedure to determine poles location 1. 2. 3. Routh-Hurwitz criterion determines if any roots of polynomial lie outside the LHP without calculating the roots. Calculation of the exact location of the roots analytically. Calculation of the exact location of the roots using digital computer. Let us consider a real polynomial Qn(s)=(s–pn) (s–pn – 1) (s–pn – 2)…(s–p 0) = sn + an – 1 sn – 1 + an – 2 sn – 2 … + a 1 s+ a 0 . . . a 0 = (– 1)n p 0 p 1 p 3… It is obvious that if all pi lie in the LHP the all coefficient must be positive. In other words 1. If any coefficient ai=0 then not all roots are in the LHP 2. If any coefficient ai<0 then at least one root is in the LHP However, it does not mean that if all coefficients are positive then all pi lie in the LHP.

6. 1. Routh-Hurwitz Stability Criterion Routh-Hurwitz criterion applies to polynomial Where Qn(s) = an sn + an – 1 sn – 1 + … + a 1 s+ a 0 Step to apply Routh-Hurwitz criterion: Step 1. Create Routh array as follow Step 2. sn an an – 2 an – 4 an – 6 … sn – 1 an – 3 an – 5 an – 2 … Count the sign change in column 1 of the array. The roots lie in the RHP = The count result. sn – 2 b 1 b 2 b 3 b 4 There are 3 cases sn – 3 c 1 c 2 c 3 c 4 case 1 no zero appear . . . Example: Q(s) = s 3 + s 2 +2 s+ 8 s 2 k 1 s 1 l 1 s 0 m 1 k 2 s 3 s 2 s 1 s 0 1 2 1 8 – 6 8 2 sign change 2 roots lie in RHP

6. 1. Routh-Hurwitz Stability Criterion Case 2 first element of a row is zero Q(s) = s 5 + 2 s 4 + 2 s 3 + 4 s 2 +11 s+ 10 s 5 1 2 11 s 4 2 4 10 s 3 /0 6 is a small number s 2 – 12/ 10 s 1 6 s 1 10 2 sign change 2 roots lie in RHP Case 3 all elements of a row is zero Q(s)= s 5 + s 4 + s 3 + s 2 +2 s 5 s 4 s 3 1 1 0 2 2 A case 3 polynomial contains even polynomials, called auxiliary polynomial, as a factor. The row above the zero row indicates the auxiliary polynomial. Thus the aux polynomial of s 5 + s 4 + s 3 + s 2 +2 s +2 is Qa = s 4 +s 2 +2. Two method available to solve this problem. Method 1 First factorized the polynomial and analyze each factor individually. For the above polynomial we have s 5 + s 4 + s 3 + s 2 +2 s +2 = (s+1)(s 4 +s 2 +2) We then create Routh array for s+1 and for s 4+s 2+2 Method 2 Differentiate the aux polynomial. The coefficient of the result replaces the zero row. Thus the coefficient of 4 s 3 + 2 s replaces the zero or s 3 4 2

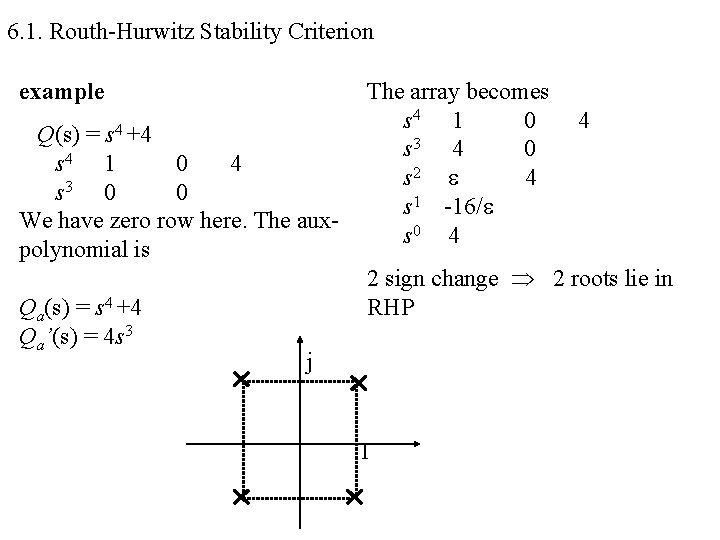
6. 1. Routh-Hurwitz Stability Criterion example s 4 +4 Q(s) = s 4 1 0 4 s 3 0 0 We have zero row here. The auxpolynomial is Qa(s) = s 4 +4 Qa’(s) = 4 s 3 The array becomes s 4 1 0 s 3 4 0 s 2 4 s 1 -16/ s 0 4 4 2 sign change 2 roots lie in RHP j 1

6. 1. Routh-Hurwitz Stability Criterion example We have control system as follow compensator plant However we have to check the stability, and we will use Routh-Hurwitz criterion The CE is found to be K s 3 + 4 s 2 +5 s+ 2+2 K = 0 The array becomes Suppose that, for constant input, we want ess<2%. The position error constant Kp is s 3 1 5 s 2 4 2+2 K s 1 (18 -2 K)/4 K<9 s 0 2 + 2 K K>-1 Here for stability requirement we must have -1<K<9 Steady state error is ess =1/(1+K) < 2%, thus K > 49. We conclude that, using proportional compensator, our requirement to have ess<2% can not be satisfied.

6. 1. Routh-Hurwitz Stability Criterion example To overcome the previous problem we have to use PI controller compensator plant KP+ KI /s s 2 (18 -2 KP)/4 s 1 c 2 KI KI > 0 s 0 2 KI where Using this controller ess= 0. We will find the values of KP and KI to assure the stability. The CE is found to be s 4 +4 s 3 + 5 s 2 +(2+2 KP)5 s+ 2 KI = 0 The array becomes If we choose KP=3<9 then c = (24 -8 KI)/3)>0 Thus s 4 1 5 s 3 4 2+2 KP 2 KI KP<9 0< KI <30

6. 1. Routh-Hurwitz Stability Criterion For the first order the general CE is Q(s) = a 1 s+ a 0 The Routh array is s 1 a 1 s 0 a 0 For the second order the general CE is Q(s) = a 2 s 2 +a 1 s+ a 0 The Routh array is s 2 a 0 s 1 a 1 s 0 a 0 Hence for the first and second order system, the necessary and sufficient condition for stability is that all the coefficient of characteristic polynomial must be of the same sign

6. 2 Roots of the CE • The RH criterion allows us to determine stability without finding the roots of the CE. • The stability can also be determined by finding the roots of the CE • • For first and second order finding the roots is trivial. For third order algebraic methods are available • For higher order numerical methods are required • One disadvantage of numerical methods is that all parameters must be assigned numerical value • Finding the range of parameter becomes more difficult when numerical methods is used. • The 1 st and 2 nd order system, its stability can be determined by the sign of the coefficient. 6. 3. Stability by Simulation § § § An obvious method for determining stability is by simulation. First system is simulated then the output observed for typical inputs. The stability then become evident. For nonlinear and time varying system, simulation may be the only way. There are no general way for analyzing nonlinear and/or time varying system. Care must be taken to ensure the accurat numerical integration