STA 517 Chp 5 Logistic Regression 1 5

STA 517 – Chp 5 Logistic Regression 1 5. 5 Fitting logistic regression models

STA 517 – Chp 5 Logistic Regression 2

STA 517 – Chp 5 Logistic Regression 3

STA 517 – Chp 5 Logistic Regression 4

STA 517 – Chp 5 Logistic Regression 5

STA 517 – Chp 5 Logistic Regression 6

STA 517 – Chp 5 Logistic Regression 7

STA 517 – Chp 5 Logistic Regression 8

STA 517 – Chp 5 Logistic Regression 9

STA 517 – Chp 5 Logistic Regression 10

STA 517 – Chp 5 Logistic Regression 11

STA 517 – Chp 5 Logistic Regression 12 proc iml; /*simulate data - true parameters*/ p=4; beta={1, 0, -2, -1}; NN=100; y=j(NN, 1, 0); n=j(NN, 1, 1); /*simulate model matrix*/ x=j(NN, 1, 1)||RANDNORMAL(NN, j(1, p-1, 0), 2*I(p-1)); /*simulate response*/ prob=exp(x*beta)/(1+exp(x*beta)); do i=1 to NN; if rand('UNIFORM')<prob[i] then y[i]=1; else y[i]=0; end; /*end simulate data*/

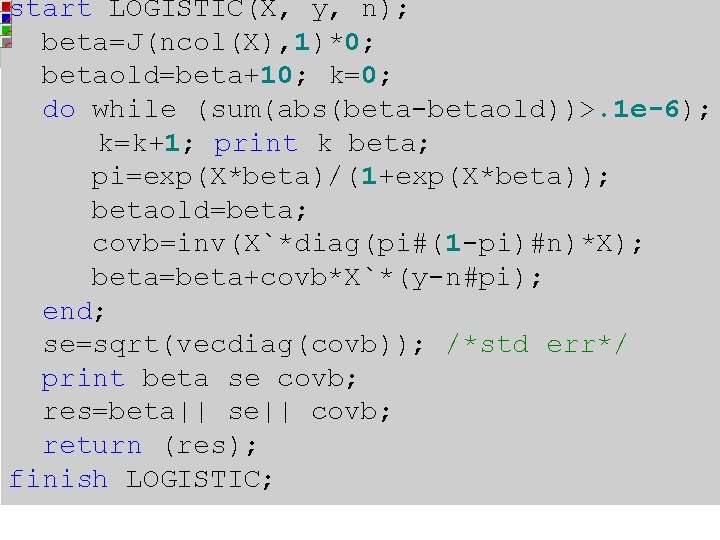
STA 517 – Chp 5 Logistic Regression /*Newton Raphson method to logistic regression*/ start LOGISTIC(X, y, n); beta=J(ncol(X), 1)*0; betaold=beta+10; k=0; do while (sum(abs(beta-betaold))>. 1 e-6); k=k+1; print k beta; pi=exp(X*beta)/(1+exp(X*beta)); u=X`*(y-n#pi); W=diag(pi#(1 -pi)#n); H=-(X`*W*X); betaold=beta; beta=beta-inv(H)*u; end; covb=-inv(H); se=sqrt(vecdiag(covb)); /*std err*/ print beta se covb; res=beta|| se|| covb; return (res); finish LOGISTIC; res=LOGISTIC(X, y, n); 13

start LOGISTIC(X, y, n); STA 517 – Chp 5 Logistic Regression 14 beta=J(ncol(X), 1)*0; betaold=beta+10; k=0; do while (sum(abs(beta-betaold))>. 1 e-6); k=k+1; print k beta; pi=exp(X*beta)/(1+exp(X*beta)); betaold=beta; covb=inv(X`*diag(pi#(1 -pi)#n)*X); beta=beta+covb*X`*(y-n#pi); end; se=sqrt(vecdiag(covb)); /*std err*/ print beta se covb; res=beta|| se|| covb; return (res); finish LOGISTIC;

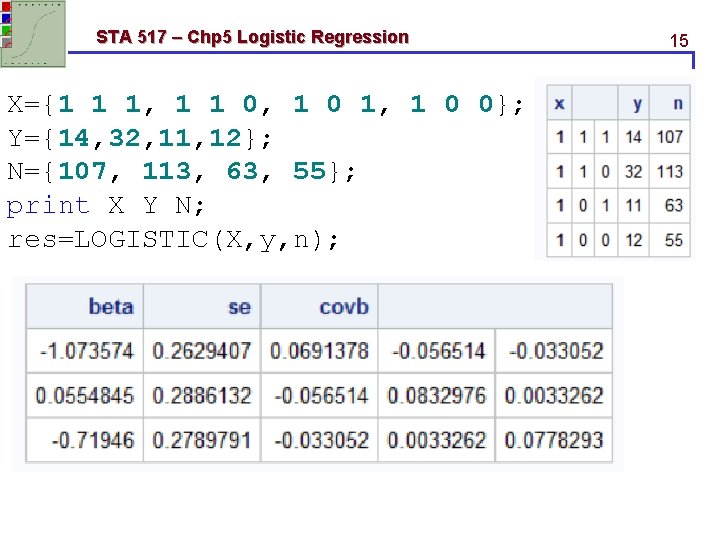
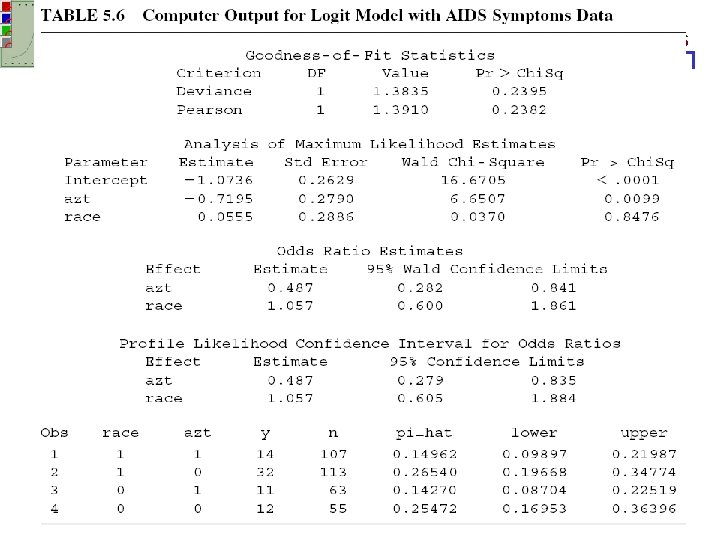
STA 517 – Chp 5 Logistic Regression X={1 1 1, 1 1 0, 1 0 1, 1 0 0}; Y={14, 32, 11, 12}; N={107, 113, 63, 55}; print X Y N; res=LOGISTIC(X, y, n); 15

STA 517 – Chp 5 Logistic Regression 16

STA 517 – Chp 5 Logistic Regression 17

STA 517 – Chp 5 Logistic Regression 18