STA 517 Chp 4 Introduction to Generalized Linear








































- Slides: 42

STA 517 – Chp 4 Introduction to Generalized Linear Models 4. 6 Fitting generalized linear models q Newton-Raphson method q Fisher scoring method 1

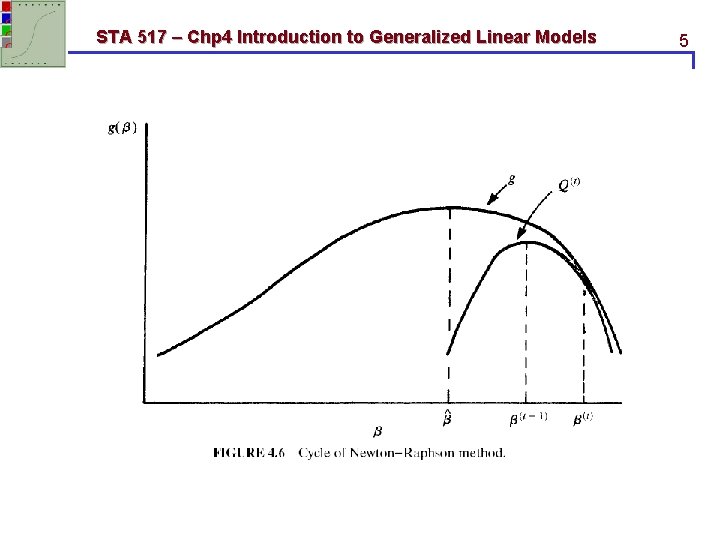
STA 517 – Chp 4 Introduction to Generalized Linear Models 4. 6. 1 Newton-Raphson method 2

STA 517 – Chp 4 Introduction to Generalized Linear Models 3

STA 517 – Chp 4 Introduction to Generalized Linear Models 4

STA 517 – Chp 4 Introduction to Generalized Linear Models 5

STA 517 – Chp 4 Introduction to Generalized Linear Models 6

STA 517 – Chp 4 Introduction to Generalized Linear Models 7

STA 517 – Chp 4 Introduction to Generalized Linear Models SAS code /*Newton-Raphson*/ proc IML; y=20; n=100; u=1: 10; H=1: 10; b[1]=0. 1; do i=1 to 10; H[i+1]=-y/b[i]**2 -(n-y)/(1 -b[i])**2; u[i+1]=(y-n*b[i])/(b[i]*(1 -b[i])); b[i+1]=b[i]-1/H[i+1] *u[i+1]; end; print b; 8

STA 517 – Chp 4 Introduction to Generalized Linear Models 4. 6. 2 Fisher scoring method 9

STA 517 – Chp 4 Introduction to Generalized Linear Models 10

STA 517 – Chp 4 Introduction to Generalized Linear Models 11

STA 517 – Chp 4 Introduction to Generalized Linear Models 12

STA 517 – Chp 4 Introduction to Generalized Linear Models 13 Recall 4. 4. 5 Likelihood equations for binomial GLMs

STA 517 – Chp 4 Introduction to Generalized Linear Models 14

STA 517 – Chp 4 Introduction to Generalized Linear Models 15 /*fit logistic regression*/ proc iml; /*simulate data - true parameters*/ p=4; beta={1, 0, -2, -1}; NN=100; y=j(NN, 1, 0); n=j(NN, 1, 1); /*simulate model matrix*/ x=j(NN, 1, 1)||RANDNORMAL(NN, j(1, p-1, 0), 2*I(p-1)); /*simulate response*/ prob=exp(x*beta)/(1+exp(x*beta)); do i=1 to NN; if rand('UNIFORM')<prob[i] then y[i]=1; else y[i]=0; end; /*end simulate data*/

STA 517 – Chp 4 Introduction to Generalized Linear Models Define likelihood equations/global search start F_GLOBAL(beta) global(y, n, x); ff=x`*(n#(y-1/(1+exp(-x*beta`)))); f=sum(ff#ff); /*likelihood eqn*/ return(f); finish F_GLOBAL; call NLPNMS(rc, b, "F_GLOBAL", beta`); err=F_GLOBAL(b); print err b; /*beta hat*/ 16

STA 517 – Chp 4 Introduction to Generalized Linear Models Estimate and SE pihat=exp(x*b`)/(1+exp(x*b`)); W=diag(pihat#(1 -pihat)#n); covb=inv(X`*W*X); se=sqrt(diag(covb)); /*std err*/ print covb se; 17

STA 517 – Chp 4 Introduction to Generalized Linear Models 18 Save data and compared with Proc logistic alldat=y||n||x; names={y n intercept x 1 x 2 x 3 x 4 x 5}; create dat 1 from alldat [colname=names]; append from alldat; close dat 1; /*compare to logistic procedure*/ proc logistic data=dat 1; model y/n=x 1 -x 3/covb; run;

STA 517 – Chp 4 Introduction to Generalized Linear Models 19 Recall 4. 4. 7 Likelihood equations and covariance matrix for Poisson loglinear model

STA 517 – Chp 4 Introduction to Generalized Linear Models 20 /*fit log linear*/ proc iml; /*simulate data - parameters*/ p=4; beta={. 5, -. 2, -. 3}; NN=100; y=j(NN, 1, 0); /*simulate model matrix*/ x=j(NN, 1, 1)||RANDNORMAL(NN, j(1, p-1, 0), I(p -1)); /*simulate response*/ y=round(exp(x*beta)); print x y; /*end simulate data*/

STA 517 – Chp 4 Introduction to Generalized Linear Models start F_GLOBAL(beta) global(y, x); ff=x`*(y-exp(x*beta`)); f=sum(ff#ff); /*likelihood eqn*/ return(f); finish F_GLOBAL; call NLPNMS(rc, b, "F_GLOBAL", beta`); err=F_GLOBAL(b); print err b; /*beta hat*/ muhat=exp(x*b`); W=diag(muhat); covb=inv(X`*W*X); se=sqrt(diag(covb)); /*std err*/ print covb se; 21

STA 517 – Chp 4 Introduction to Generalized Linear Models 22 alldat=y||x; names={y intercept x 1 x 2 x 3 x 4 x 5}; create dat 2 from alldat [colname=names]; append from alldat; close dat 2; /*compare to log linear model in genmod*/ proc genmod data=dat 2; model y=x 1 -x 3/dist=POISSON link=log; run;

STA 517 – Chp 4 Introduction to Generalized Linear Models 23 4. 7 Quasi-likelihood and generalized linear models

STA 517 – Chp 4 Introduction to Generalized Linear Models 24

STA 517 – Chp 4 Introduction to Generalized Linear Models 25

STA 517 – Chp 4 Introduction to Generalized Linear Models 4. 7. 2 Overdispersion for Poisson GLMs and quasi-likelihood 26

STA 517 – Chp 4 Introduction to Generalized Linear Models 27

STA 517 – Chp 4 Introduction to Generalized Linear Models 28

STA 517 – Chp 4 Introduction to Generalized Linear Models 29

STA 517 – Chp 4 Introduction to Generalized Linear Models 30

STA 517 – Chp 4 Introduction to Generalized Linear Models 31

STA 517 – Chp 4 Introduction to Generalized Linear Models 32

STA 517 – Chp 4 Introduction to Generalized Linear Models 33

STA 517 – Chp 4 Introduction to Generalized Linear Models 34

STA 517 – Chp 4 Introduction to Generalized Linear Models 35

STA 517 – Chp 4 Introduction to Generalized Linear Models 36

STA 517 – Chp 4 Introduction to Generalized Linear Models 4. 7. 4 Teratology overdispersion example 37

STA 517 – Chp 4 Introduction to Generalized Linear Models 38

STA 517 – Chp 4 Introduction to Generalized Linear Models 39

STA 517 – Chp 4 Introduction to Generalized Linear Models 40

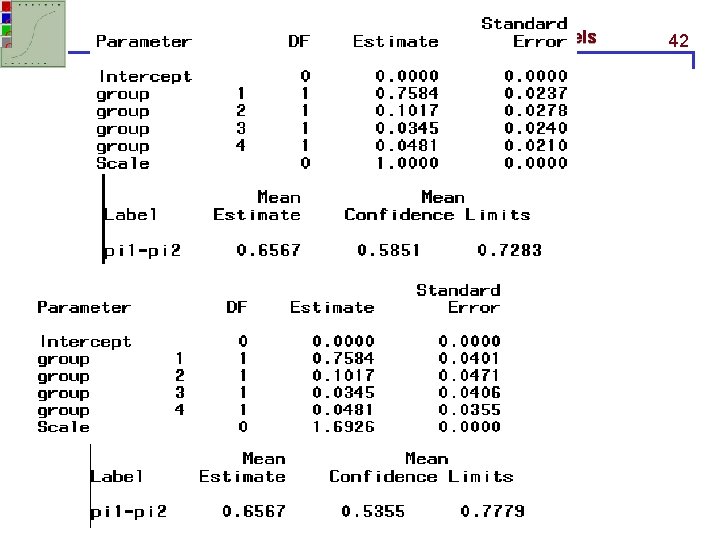
STA 517 – Chp 4 Introduction to Generalized Linear Models 41 SAS code data moore; input litter group n y @@; datalines; 1 1 10 1 2 1 11 4 3 1 12 9 4 1 4 4 5 1 10 10 … 55 4 14 1 56 4 8 0 58 4 17 0 ; proc genmod; class group; model y/n = group / dist = bin link = identity noint; estimate ‘pi 1 - pi 2 ’ group 1 -1 0 0; proc genmod; class group; model y/n = group / dist = bin link = identity noint scale = pearson;

STA 517 – Chp 4 Introduction to Generalized Linear Models 42