St Patricks Primary School Mathematics Learning in Stage

St Patrick’s Primary School Mathematics Learning in Stage 2 Judy Anderson The University of Sydney judy. anderson@sydney. edu. au

What issues/concerns do you have about mathematics learning in Stage 2?

How do you plan for learning in mathematics?

The Australian Curriculum: Some of the key decisions u Mathematics success creates opportunities and all should have access to those opportunities u The curriculum should prioritise teacher decision making u The curriculum should foster depth and important ideas rather than breadth u Students can be challenged within basic topics, including the advanced students

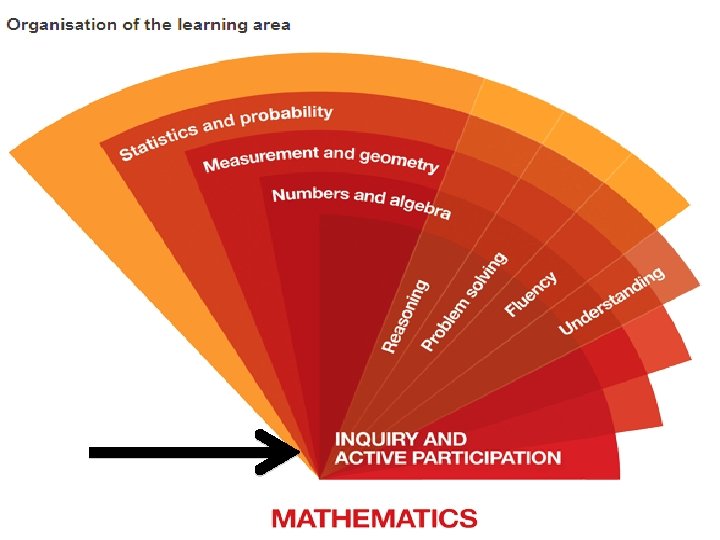
There are 3 content strands u Number and algebra u Measurement u Statistics and geometry and probability

… and 4 proficiency strands u Understanding u Fluency u Problem solving u Reasoning

Understanding Fluency Students build a robust knowledge of adaptable and transferable mathematical concepts. They make connections between related concepts and progressively apply the familiar to develop new ideas. Students develop skills in choosing appropriate procedures, carrying out procedures flexibly, accurately, efficiently and appropriately, and recalling factual knowledge and concepts readily.

Problem solving Students develop the ability to make choices, interpret, formulate, model and investigate problem situations, and communicate solutions effectively. Reasoning Students develop an increasingly sophisticated capacity for logical thought and actions, such as analysing, proving, evaluating, explaining, inferring, justifying, and generalising.

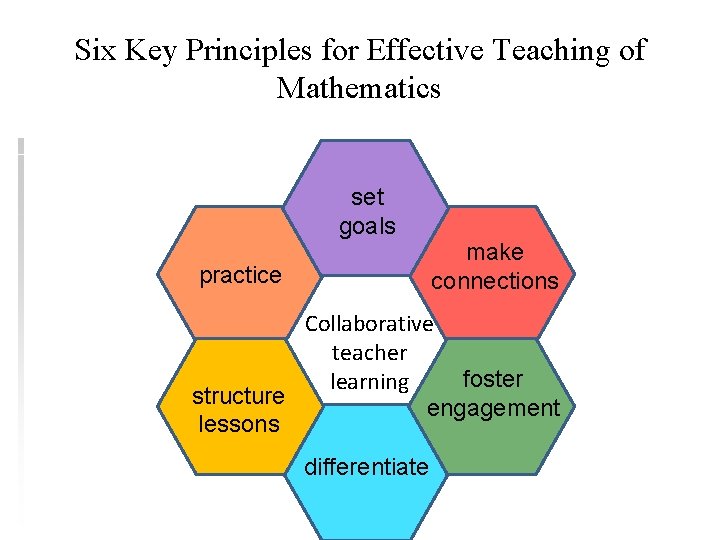
Our Plan (September/November) u Review rich tasks u Link to the curriculum (Australian/NSW) – content AND proficiences u Consider the Six Key Principles for Effective Teaching of Mathematics u Design ‘good lessons’ u Trial/refine/retrial our ideas u Share/collaborate with colleagues

What are rich tasks? foster engagement

Number and Algebra: Make or lose 100 Hundreds chart patterns and relationships Choose your path Multi lotto Colour-in-fractions Posing problems from photos Measurement and geometry: Money trails Measuring angles in the classroom Statistics and Probability The language of chance What’s in the bag? Dice Differences Some Rich Tasks

Number and Algebra

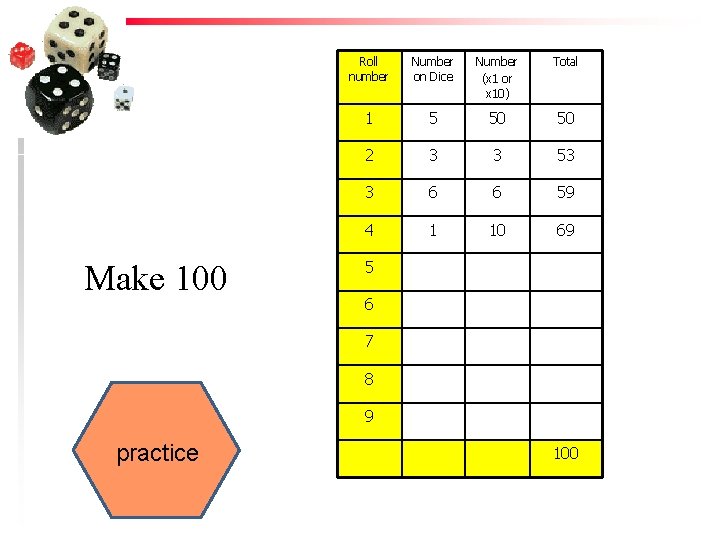
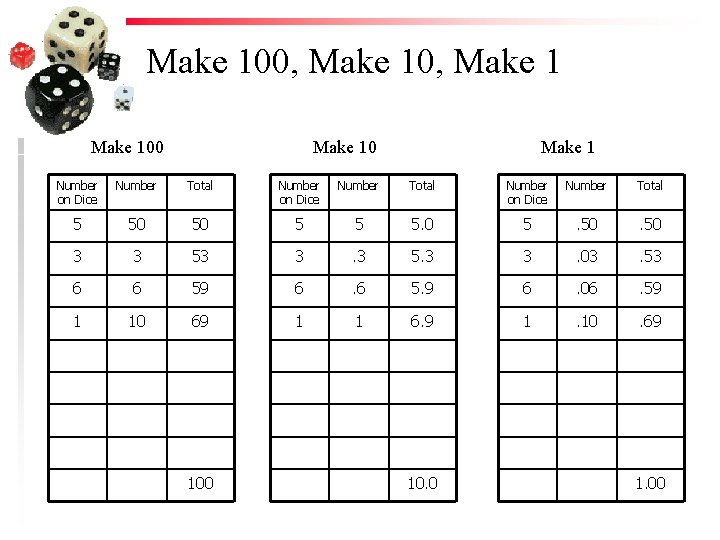
Make 100 Roll number Number on Dice Number (x 1 or x 10) Total 1 5 50 50 2 3 3 53 3 6 6 59 4 1 10 69 5 6 7 8 9 practice 100

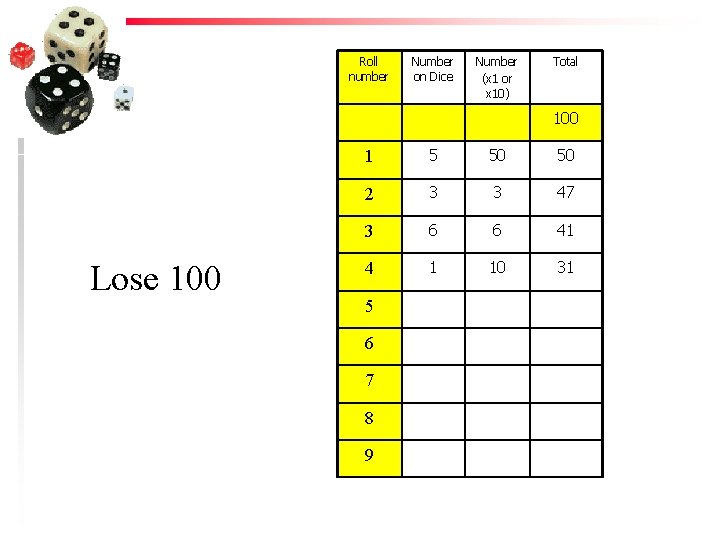
Roll number Number on Dice Number (x 1 or x 10) Total 100 Lose 100 1 5 50 50 2 3 3 47 3 6 6 41 4 1 10 31 5 6 7 8 9

Make 100, Make 100 Make 1 Number on Dice Number Total 5 50 50 5 5 5. 0 5 . 50 3 3 53 3 . 3 5. 3 3 . 03 . 53 6 6 59 6 . 6 5. 9 6 . 06 . 59 1 10 69 1 1 6. 9 1 . 10 . 69 100 10. 0 1. 00

Some questions u What is the mathematical purpose of that task? u What is the pedagogical purpose of that task? u How can this be communicated to students? u What mathematical proficiencies (actions) can be addressed by working on that task? set goal s

Six Key Principles for Effective Teaching of Mathematics set goals practice make connections Collaborative teacher foster learning structure engagement lessons differentiate

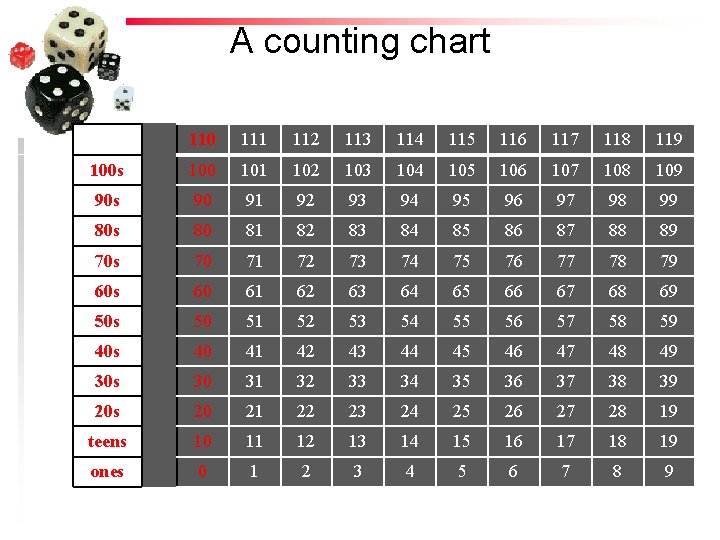
A counting chart 110 111 112 113 114 115 116 117 118 119 100 s 100 101 102 103 104 105 106 107 108 109 90 s 90 91 92 93 94 95 96 97 98 99 80 s 80 81 82 83 84 85 86 87 88 89 70 s 70 71 72 73 74 75 76 77 78 79 60 s 60 61 62 63 64 65 66 67 68 69 50 s 50 51 52 53 54 55 56 57 58 59 40 s 40 41 42 43 44 45 46 47 48 49 30 s 30 31 32 33 34 35 36 37 38 39 20 s 20 21 22 23 24 25 26 27 28 19 teens 10 11 12 13 14 15 16 17 18 19 ones 0 1 2 3 4 5 6 7 8 9

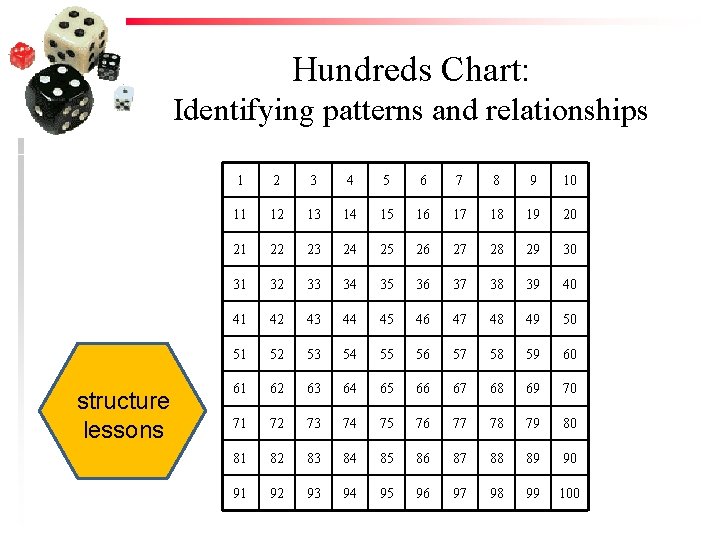
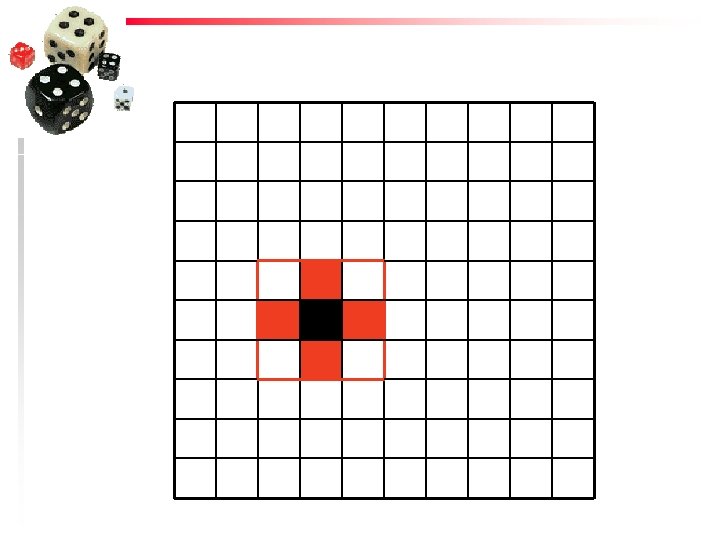
Hundreds Chart: Identifying patterns and relationships structure lessons 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100

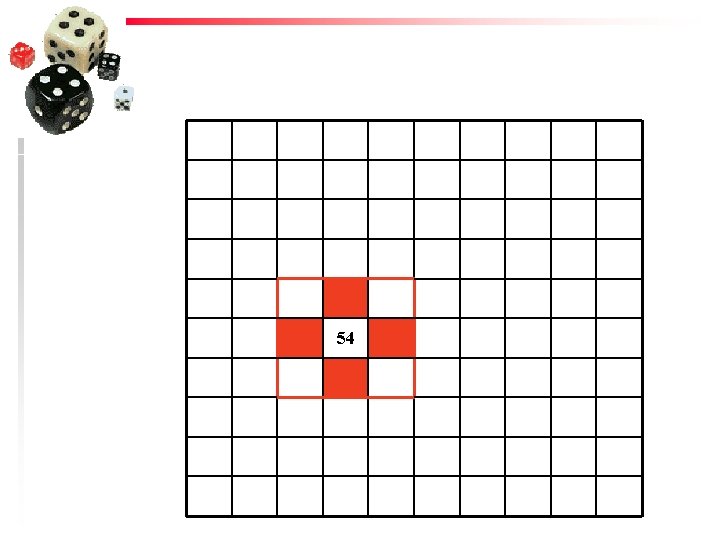
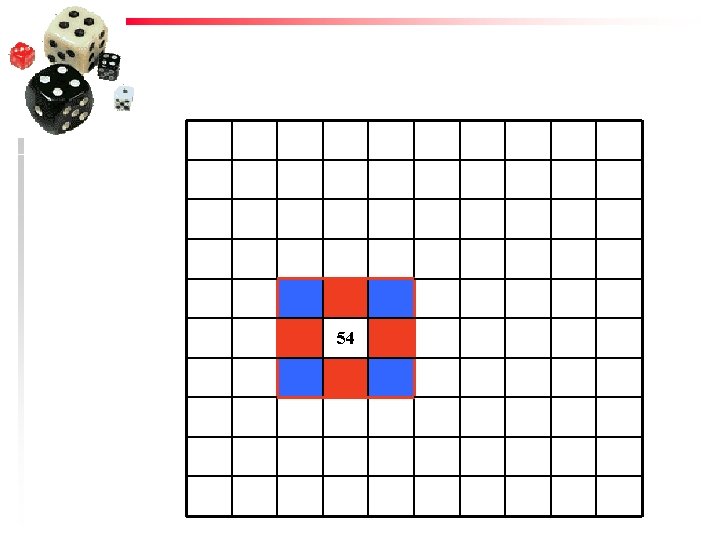
Goal Task 1. Choose any number on a hundreds chart (or calendar, …) as the first number in a pattern. 2. From this number, record the pattern of numbers going up, or down, or to the left, or to the right, or diagonally. 3. Describe the pattern in words (or represent the pattern in a table or in a diagram, or using symbols)

54

54

54

Enabling prompts u Count forwards and backwards from a given number u Write the numbers in order u What is the difference between each number u If you kept going, what is the 10 th (20 th) number in the pattern? u u u

Extending prompts 1. Pose additional questions: • If you start at 3 and count in steps of 3, will you say the number 78? How do you know? • If you start at 3 and count in steps of 5, will you say the number 71? How do you know? • Count in steps of 5 starting at 13? What patterns do you see? Would you say 72? 68? 2. Represent patterns in a number of ways (generalise using symbols) 3. Use different grids (eg calendars) to identify and describe patterns 4.

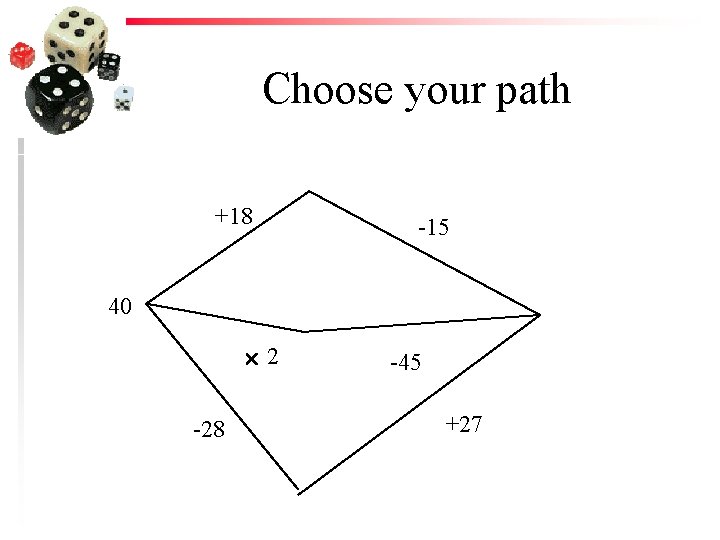
Choose your path +18 -15 40 -28 2 -45 +27

Multi Lotto (Downton et al. ) 30 On the grid, record 16 different numbers which are all answers to the multiplication facts.

1 2 3 4 5 6 7 8 9 10 1 1 2 3 4 5 6 7 8 9 10 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 How many different numbers can you choose? Which are the best numbers to choose and why? Investigate, record and represent

An Investigation: Which of the following game boards would you choose to use and why? 30 5 20 12 30 25 20 15 24 7 15 60 54 70 17 23 10 5 4 3 13 10 16 25 40 8 19 31 12 15 18 21 4 36 18 3 80 4 6 10 24 27 35 40 Now create the ‘ideal’ game board.

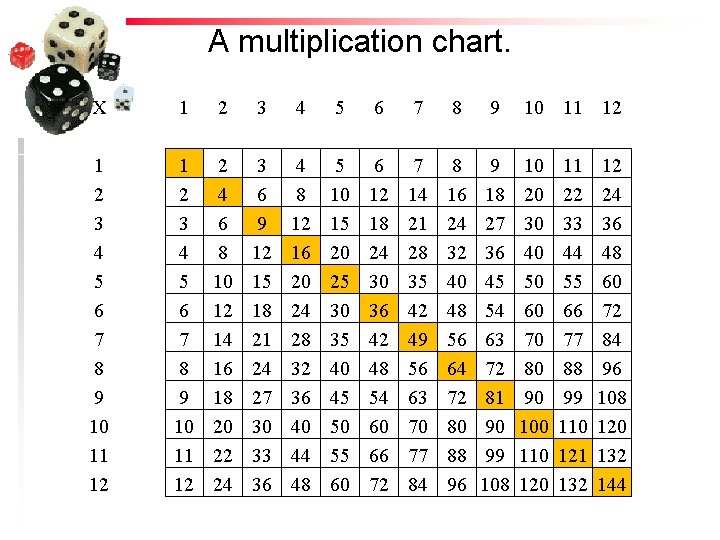
A multiplication chart. X 1 2 3 4 5 6 7 8 9 10 11 12 2 4 6 8 10 12 14 16 18 20 22 24 3 6 9 12 15 18 21 24 27 30 33 36 4 8 12 16 20 24 28 32 36 40 44 48 5 10 15 20 25 30 35 40 45 50 55 60 6 12 18 24 30 36 42 48 54 60 66 72 7 14 21 28 35 42 49 56 63 70 77 84 8 16 24 32 40 48 56 64 72 80 88 96 9 18 27 36 45 54 63 72 81 90 99 108 10 11 12 10 20 30 40 50 60 70 80 90 100 110 120 11 22 33 44 55 66 77 88 99 110 121 132 12 24 36 48 60 72 84 96 108 120 132 144

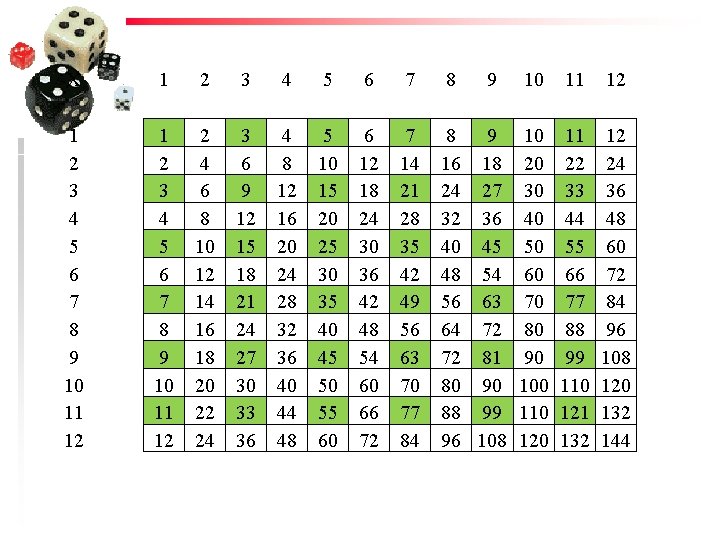
X 1 2 3 4 5 6 7 8 9 10 11 12 2 4 6 8 10 12 14 16 18 20 22 24 3 6 9 12 15 18 21 24 27 30 33 36 4 8 12 16 20 24 28 32 36 40 44 48 5 10 15 20 25 30 35 40 45 50 55 60 6 12 18 24 30 36 42 48 54 60 66 72 7 14 21 28 35 42 49 56 63 70 77 84 8 9 16 18 24 27 32 36 40 45 48 54 56 63 64 72 72 81 80 90 88 99 96 108 10 11 12 10 20 30 40 50 60 70 80 90 100 110 120 11 22 33 44 55 66 77 88 99 110 121 132 12 24 36 48 60 72 84 96 108 120 132 144

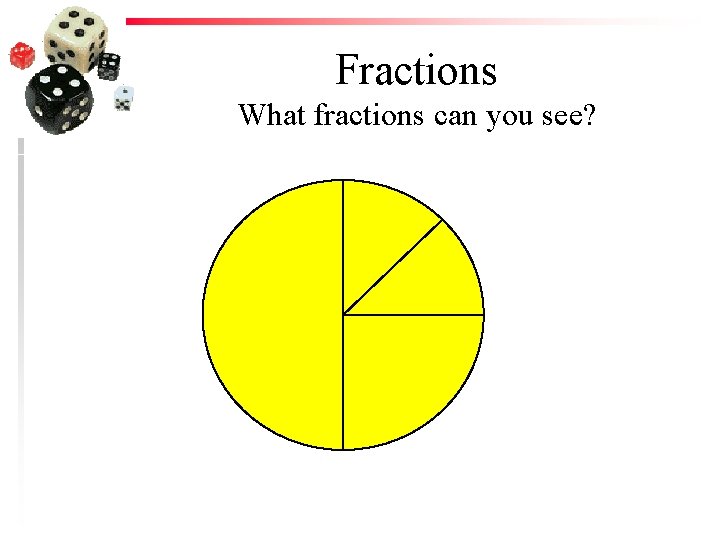
Fractions What fractions can you see?

Colour in Fractions 1. each player has a game board 2. in turns, throw the dice to make a fraction 3. colour in that fraction, or its equivalent on your board 4. the first person to colour the entire board wins. 1 ½ ½ ⅓ ¼ ⅙ ⅓ ¼ ¼

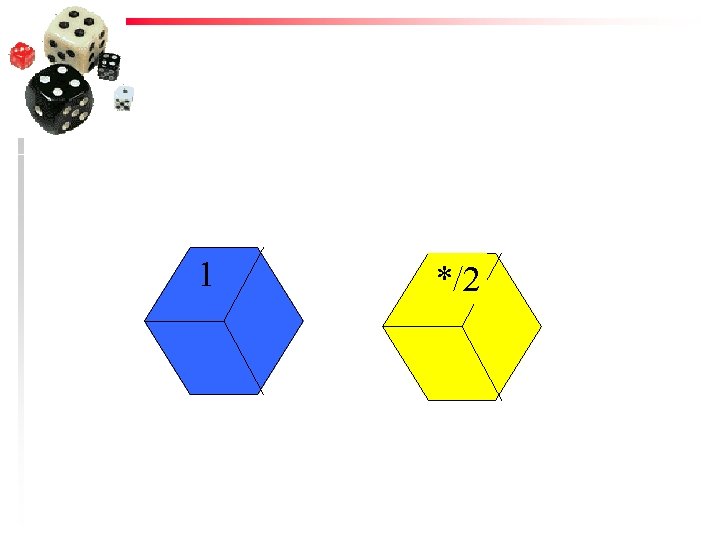
1 */2

Recording = + +

How many different ways can you make ½?

Flags

Students’ Posing Problems: Mathematics from Photographs Look at the photographs and make connections What do you notice? Write down some mathematical problems that occur to you. Now do some mathematics based on the photograph.

45

Observing, predicting and proving What patterns can you see in the following? Write your numbers in a table. Predict the next values. Draw the next shape to see if your prediction was correct.

Measurement and Geometry

Money Trails u If I made a trail of 20 cent coins from the classroom door to the school gate, how much money would I need? u How far can $10 really stretch?

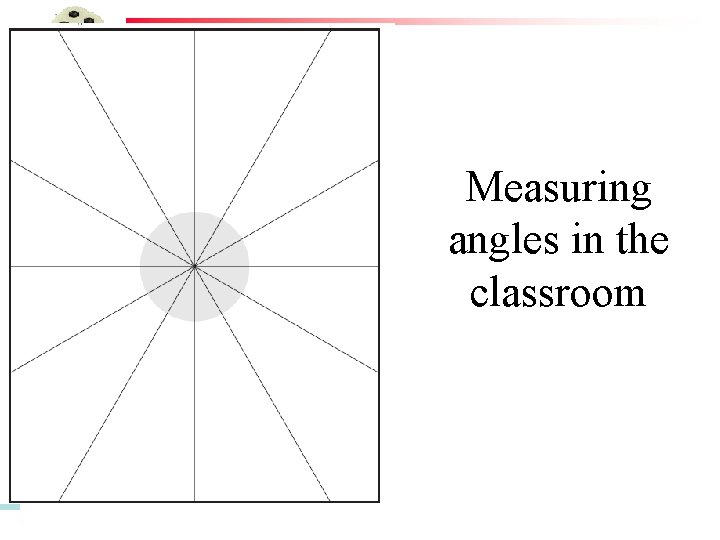
Measuring angles in the classroom

Statistics and Probability

The language of chance u u

What’s in the bag?

Dice Sums and Differences Dice Differences (throw two dice and find the difference) • Player A scores a point if the difference is 0, 1, or 2 • Player B scores a point if the difference is 3, 4, or 5 • Is this game fair? • Change the rules to make it fair – investigate, record and represent

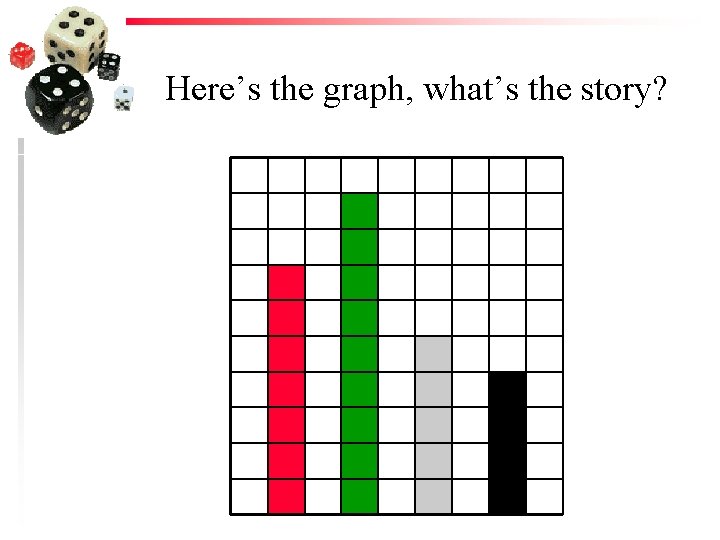
Here’s the graph, what’s the story?

Linking and Connecting Strands and KLAs

Data and Measurement • Does the tallest person have the longest stride? • Does the tallest person have the longest feet? • Are eight year olds taller than seven year olds? • Are boys feet or girls feet bigger?

Establish classroom ways of working u Examples – – of “norms” errors are part of learning all students must persist all students must be willing to justify their thinking working as a community of learners benefits everyone

Six Key Principles for Effective Teaching of Mathematics set goals practice make connections Collaborative teacher foster learning structure engagement lessons differentiate

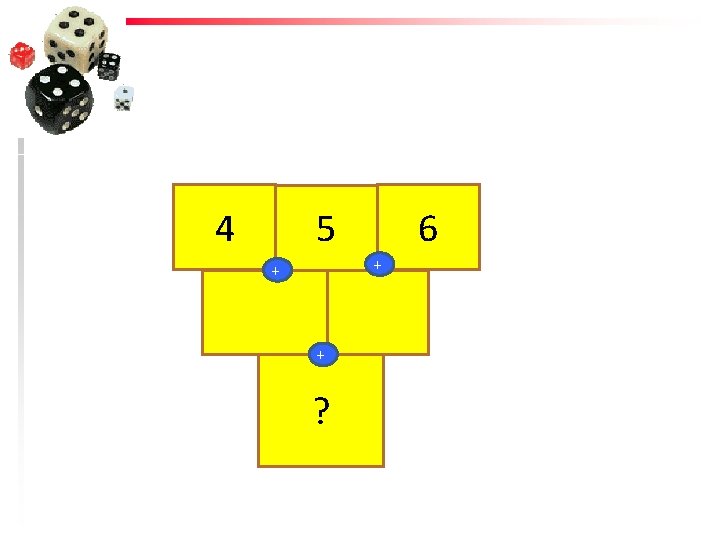
practice 3 4 + 7

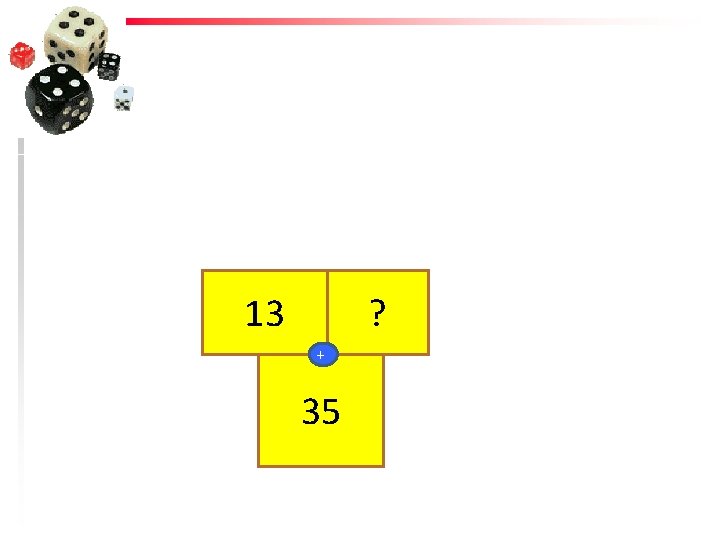
13 ? + 35

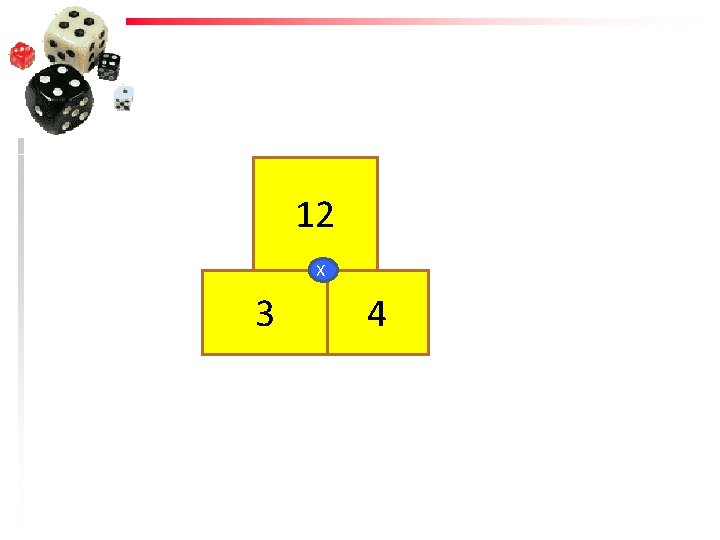
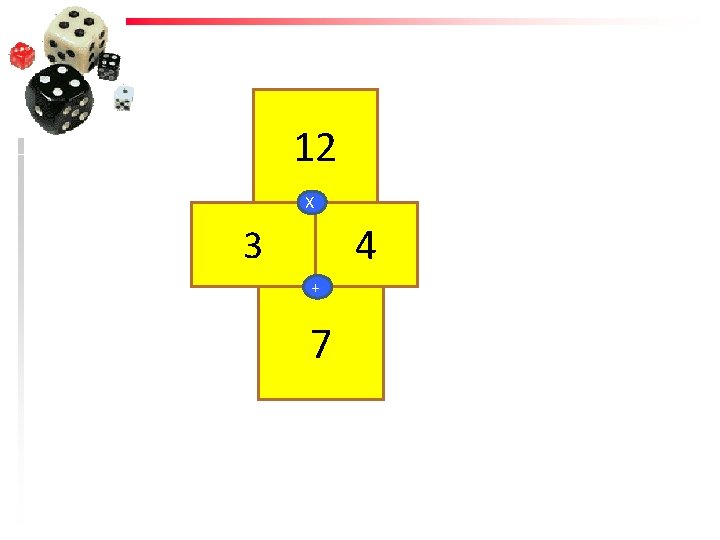
12 X 3 4

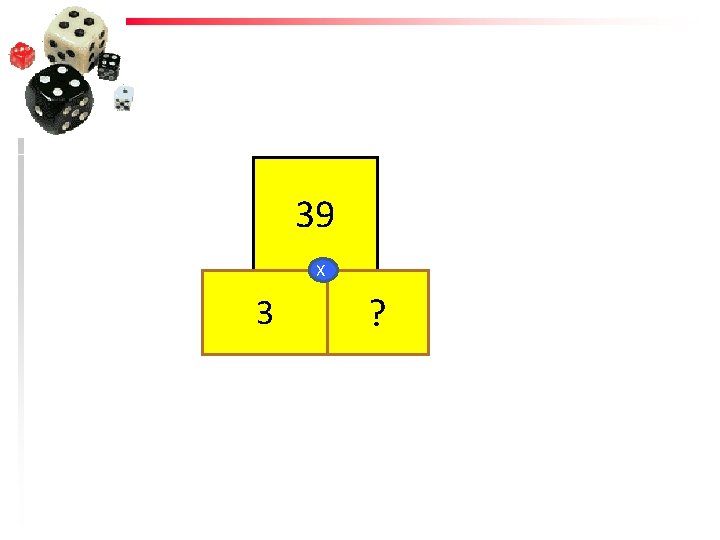
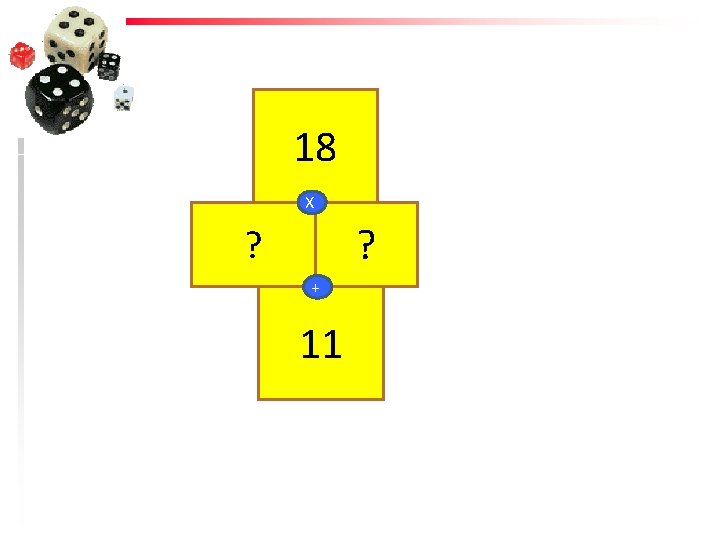
39 X 3 ?

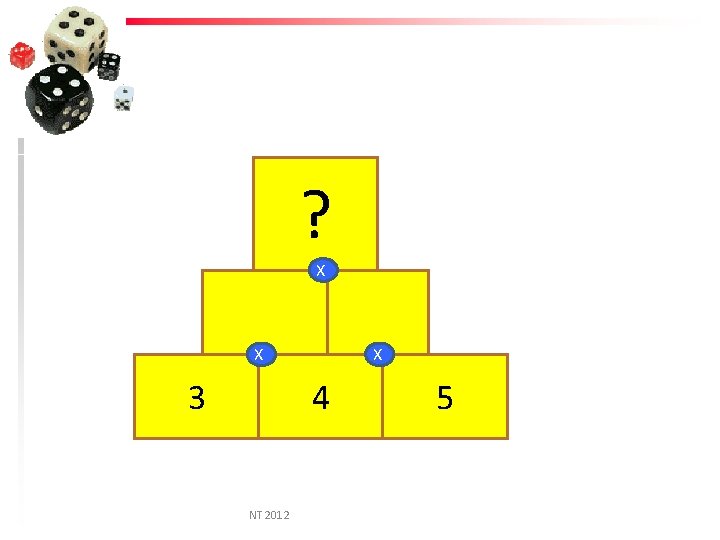
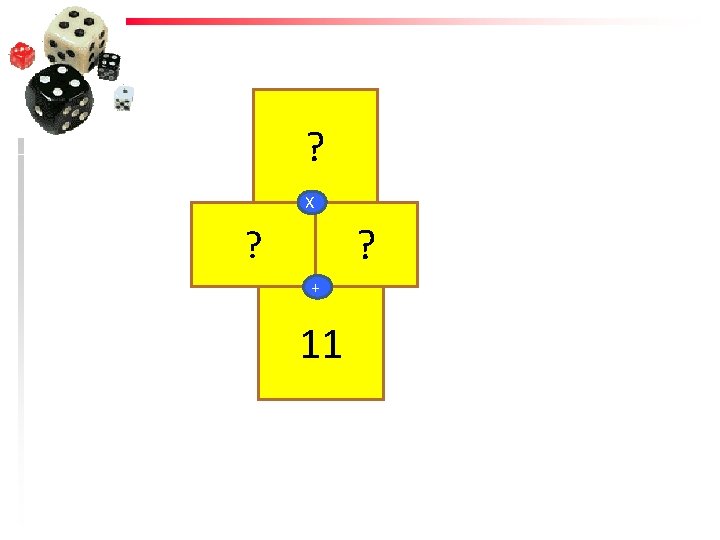
? X X 3 X 4 NT 2012 5

12 X 4 3 + 7

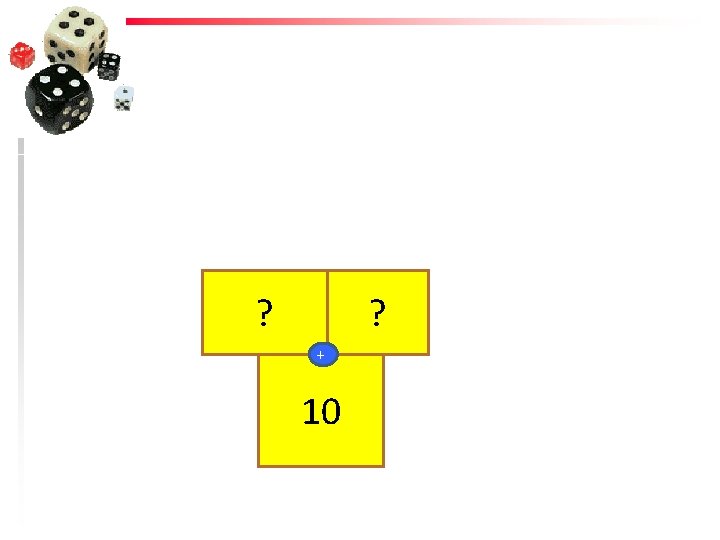
18 X ? ? + 11

What is your favourite maths Problem or Investigation? u The four 4’s problem: Use four 4’s and any mathematics operations to create as many different number sentences as you can. Try to find sentences with answers from 1 to 20. Eg, 4 + 4 + 4 = 16 (is there any number sentence with an answer of 16? )

St Patrick’s Primary School Mathematics Learning in Stage 2 Judy Anderson The University of Sydney judy. anderson@sydney. edu. au