SSA Stanford University CS 243 Winter 2006 Wei

SSA Stanford University CS 243 Winter 2006 Wei Li 1

Overview SSA Representation n SSA Construction n Converting out of SSA n Stanford University CS 243 Winter 2006 2

Static Single Assignment Each variable has only one reaching definition. n When two definitions merge, a Ф function is introduced to with a new definition of the variable. n First consider SSA for alias free variables. n Stanford University CS 243 Winter 2006 3

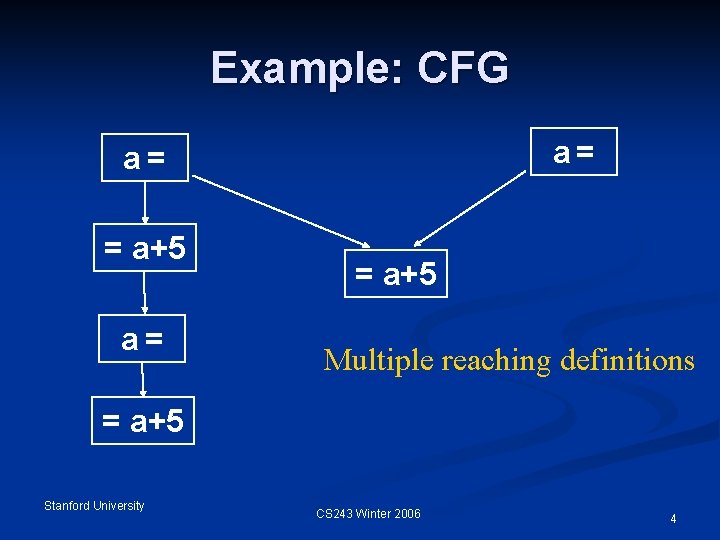
Example: CFG a= a= = a+5 Multiple reaching definitions = a+5 Stanford University CS 243 Winter 2006 4

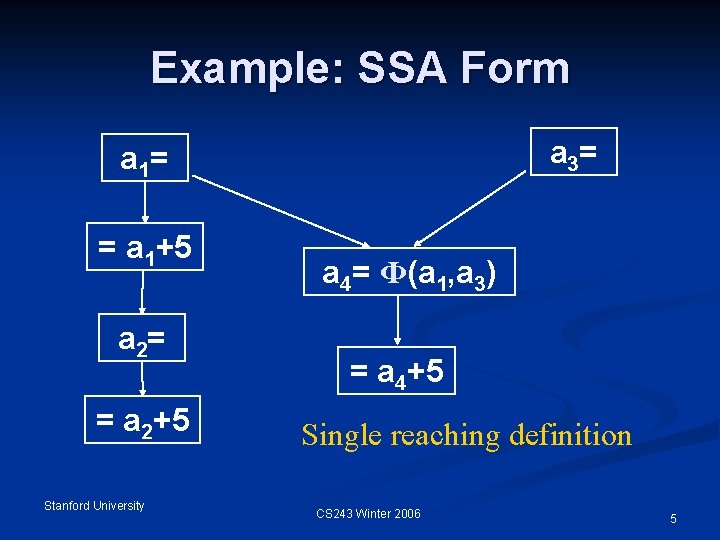
Example: SSA Form a 3= a 1= = a 1+5 a 2= = a 2+5 Stanford University a 4= Ф(a 1, a 3) = a 4+5 Single reaching definition CS 243 Winter 2006 5

Ф Functions A Ф operand represents the reaching definition from the corresponding predecessor. n The ordering of Ф operands are important for knowing from which path the definition is coming from. n Stanford University CS 243 Winter 2006 6

SSA Conditions 1. 2. 3. If two nonnull paths X →+ Z and Y →+ Z converge at node Z, and nodes X and Y contains (V =. . ), then V = Ф(V, . . , V) has been inserted at Z. Each mention of V has been replaced by a mention of Vi V and the corresponding Vi have the same value. Stanford University CS 243 Winter 2006 7

Overview SSA Representation n SSA Construction n Step 1: Place Ф statements n Step 2: Rename all variables n n Converting out of SSA Stanford University CS 243 Winter 2006 8

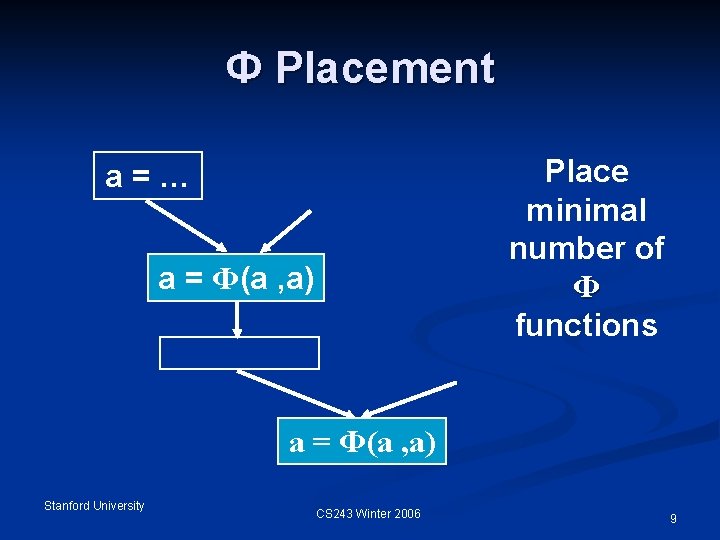
Ф Placement Place minimal number of Ф functions a=… a = Ф(a , a) Stanford University CS 243 Winter 2006 9

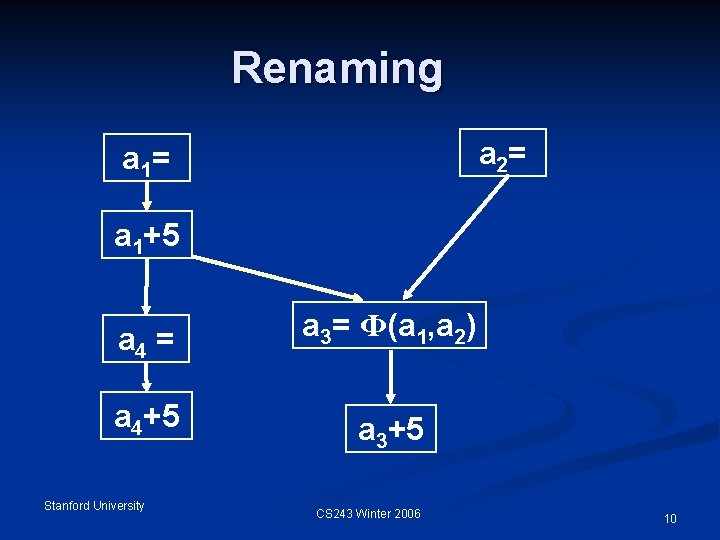
Renaming a 2= a 1+5 a 4 = a 3= Ф(a 1, a 2) a 4+5 a 3+5 Stanford University CS 243 Winter 2006 10

SSA Construction (I) n Step 1: Place Ф statements by computing iterated dominance frontier Stanford University CS 243 Winter 2006 11

CFG A control flow graph G = (V, E) n Set V contains distinguished nodes START and END n every node is reachable from START n END is reachable from every node in G. n START has no predecessors n END has no successors. n n Predecessor, successor, path Stanford University CS 243 Winter 2006 12

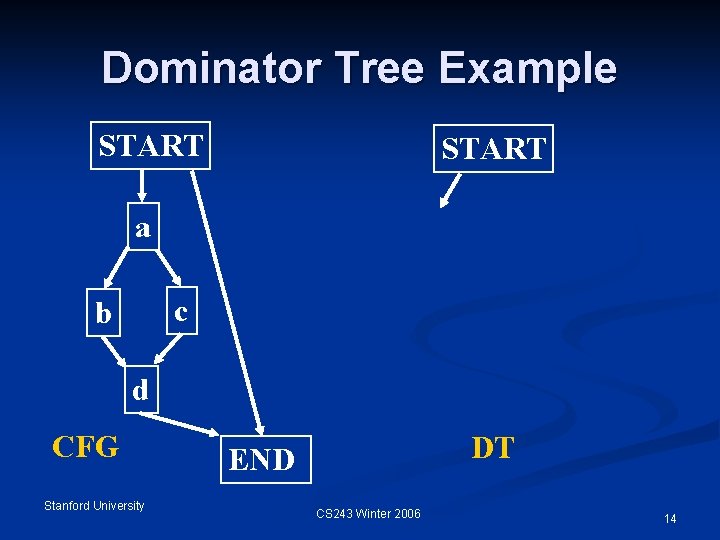
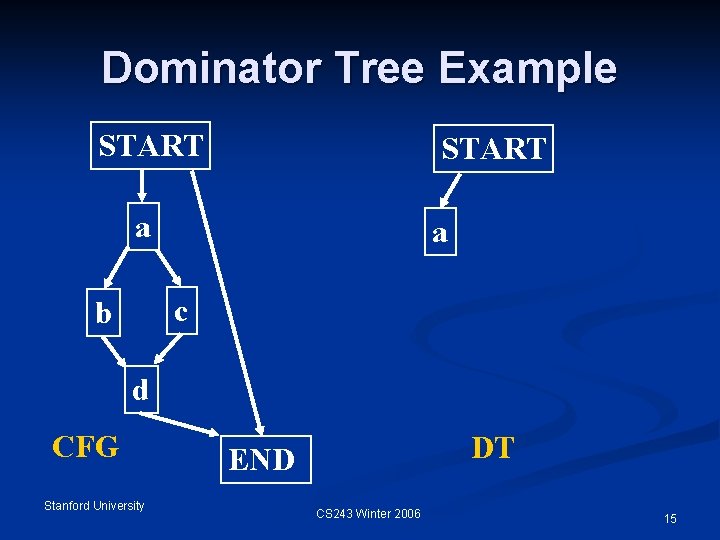
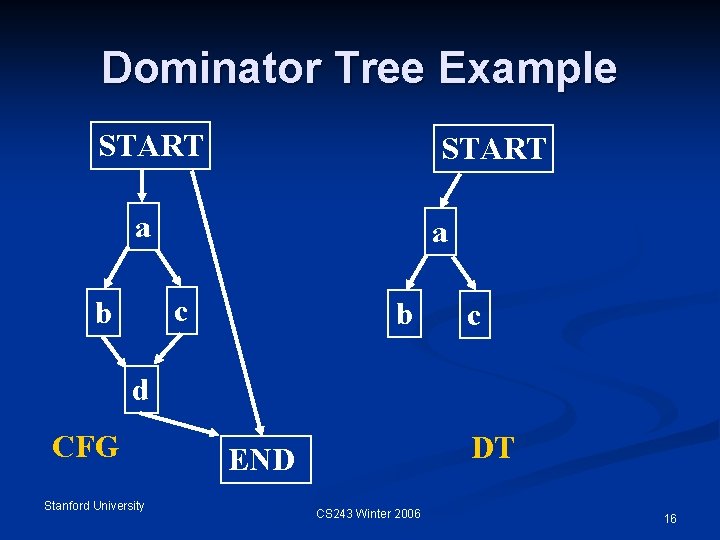
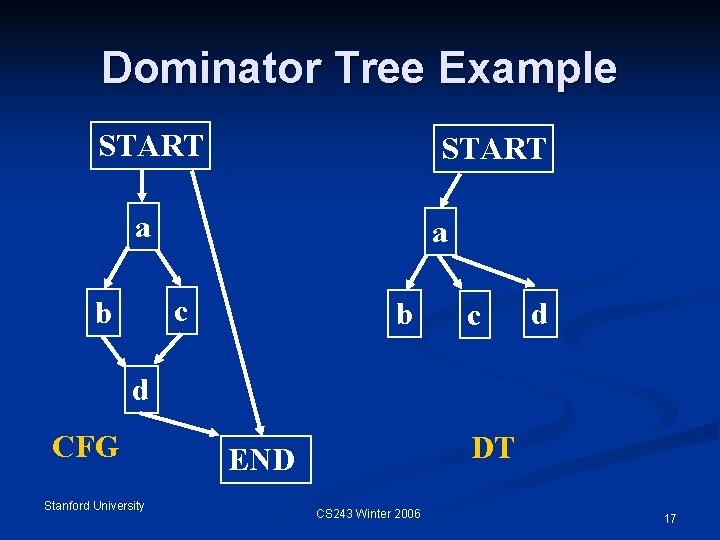
Dominator Relation If X appears on every path from START to Y, then X dominates Y. n Domination is both reflexive and transitive. n idom(Y): immediate dominator of Y n Dominator Tree n START is the root n Any node Y other than START has idom(Y) as its parent n Parent, child, ancestor, descendant n Stanford University CS 243 Winter 2006 13

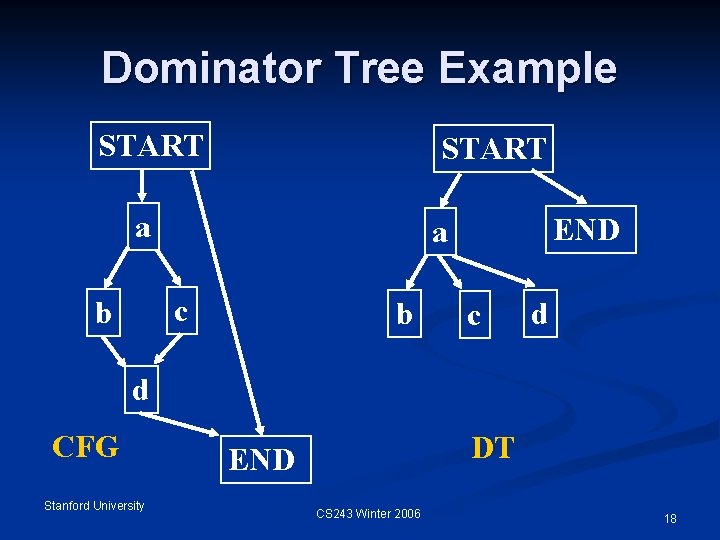
Dominator Tree Example START a c b d CFG Stanford University DT END CS 243 Winter 2006 14

Dominator Tree Example START a a c b d CFG Stanford University DT END CS 243 Winter 2006 15

Dominator Tree Example START a a c b b c d CFG Stanford University DT END CS 243 Winter 2006 16

Dominator Tree Example START a a c b b c d d CFG Stanford University DT END CS 243 Winter 2006 17

Dominator Tree Example START a c b END a b c d d CFG Stanford University DT END CS 243 Winter 2006 18

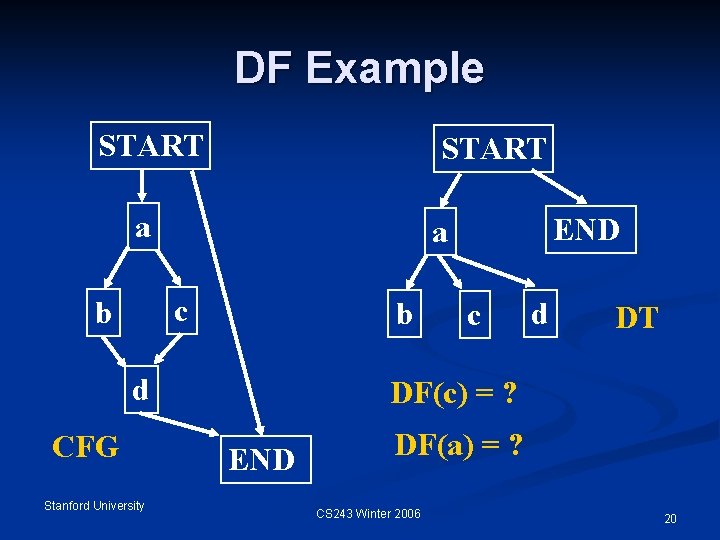
Dominance Frontier n Dominance Frontier DF(X) for node X Set of nodes Y n X dominates a predecessor of Y n X does not strictly dominate Y n Stanford University CS 243 Winter 2006 19

DF Example START a c b b d CFG Stanford University END a c d DT DF(c) = ? END DF(a) = ? CS 243 Winter 2006 20

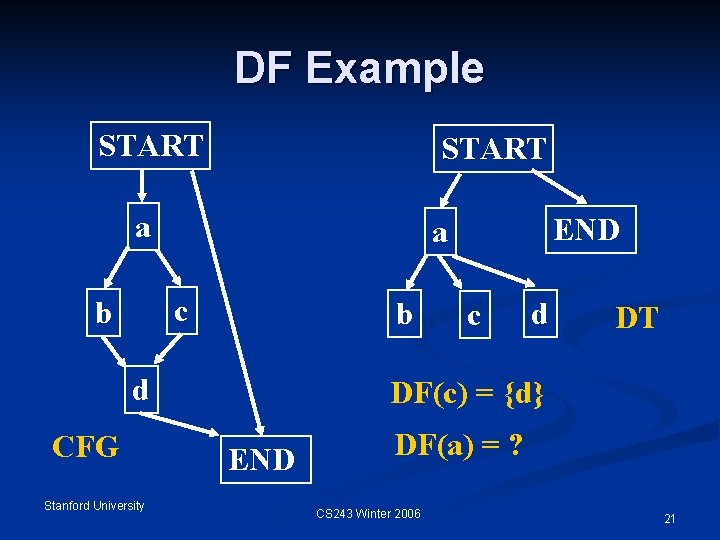
DF Example START a c b b d CFG Stanford University END a c d DT DF(c) = {d} END DF(a) = ? CS 243 Winter 2006 21

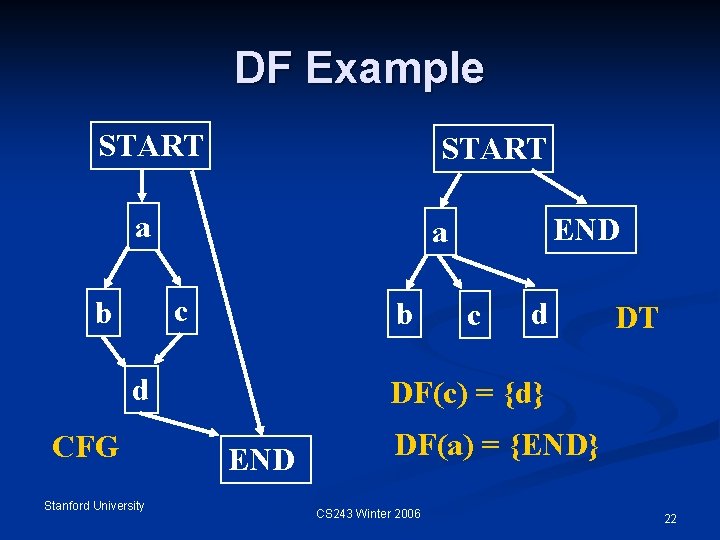
DF Example START a c b b d CFG Stanford University END a c d DT DF(c) = {d} END DF(a) = {END} CS 243 Winter 2006 22

Computing DF n DF(X) is the union of the following sets n DFlocal(X), a set of successor nodes that X doesn’t strictly dominate n E. g. n DFlocal(c) = {d} DFup(Z) for all Z є Children(X) n DFup(Z) = {Y є DF(Z) | idom(Z) doesn’t strictly dominate Y} n E. g. X = a, Z = d, Y = END Stanford University CS 243 Winter 2006 23

Iterated Dominance Frontier DF(SET) is the union of DF(X), where X є SET. n Iterated dominance frontier DF+(SET) is the limit of n n DF 1 = DF(SET) and DFi+1 = DF(SET U DFi) Stanford University CS 243 Winter 2006 24

Computing Joins n J(SET) of join nodes Set of all nodes Z n There are two nonnull CFG paths that start at two distinct nodes in SET and converge at Z. n n Iterated join J+(SET) is the limit of n n J 1 = J(SET) and Ji+1 = J(SET U Ji) J+(SET) = DF+(SET) Stanford University CS 243 Winter 2006 25

Placing Ф Functions n For each variable V Add all nodes with assignments to V to worklist W n While X in W do n n For n Stanford University each Y in DF(X) do If no Ф added in Y then n Place (V = Ф (V, …, V)) at Y n If Y has not been added before, add Y to W. CS 243 Winter 2006 26

Computational Complexity S n a Atot: total number of assignments n avrg. DF: weighted average DF size n b c d Constructing SSA takes O(Atot * avrg. DF), where n The computational complexity is O(n 2). n E Stanford University e. g. nested repeat-until loops CS 243 Winter 2006 27

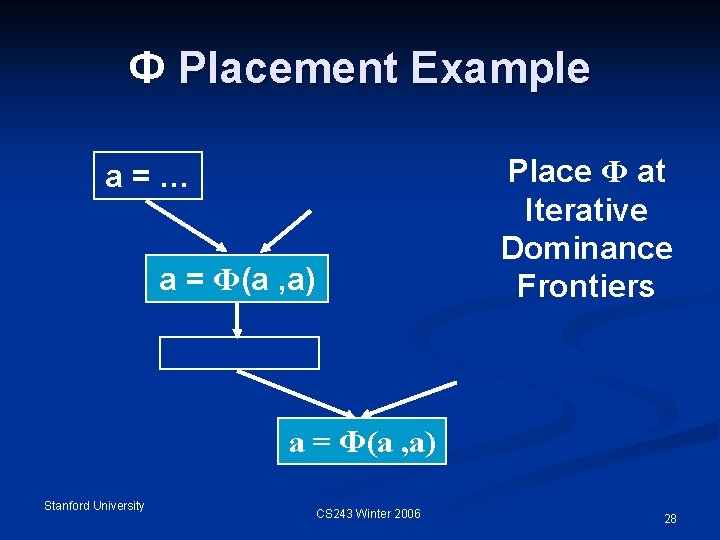
Ф Placement Example Place Ф at Iterative Dominance Frontiers a=… a = Ф(a , a) Stanford University CS 243 Winter 2006 28

SSA Construction (II) n Step 2: Rename all variables in original program and Ф functions, using dominator tree and rename stack to keep track of the current names. Stanford University CS 243 Winter 2006 29

Variable Renaming n n Rename from the START node recursively For node X n For each assignment (V = …) in X n n n Rename any use of V with the TOS of rename stack Push the new name Vi on rename stack i=i+1 Rename all the Ф operands through successor edges Recursively rename for all child nodes in the dominator tree For each assignment (V = …) in X n Pop Vi in X from the rename stack Stanford University CS 243 Winter 2006 30

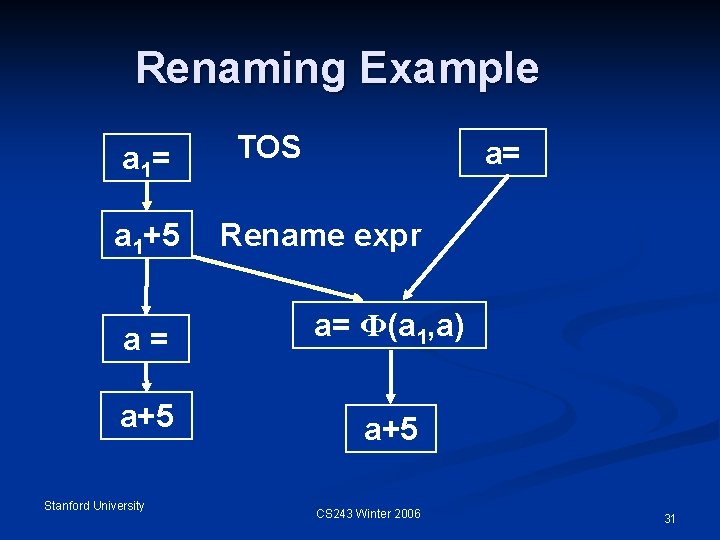
Renaming Example a 1= a 1+5 TOS a= Rename expr a= a= Ф(a 1, a) a+5 Stanford University CS 243 Winter 2006 31

Overview SSA Representation n SSA Construction n Converting out of SSA n Stanford University CS 243 Winter 2006 32

Converting Out of SSA n Mapping all Vi to V? Stanford University CS 243 Winter 2006 33

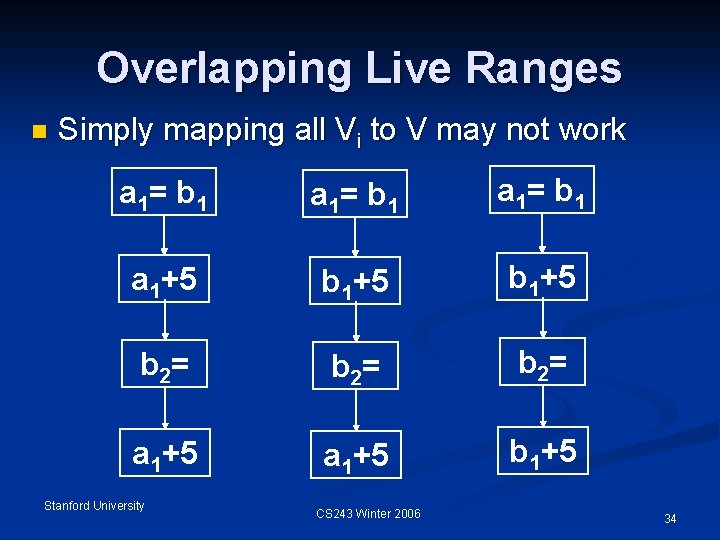
Overlapping Live Ranges n Simply mapping all Vi to V may not work a 1= b 1 a 1+5 b 2= b 2= a 1+5 b 1+5 Stanford University CS 243 Winter 2006 34

Converting Out of SSA n Option 1: coloring Compute live ranges, and assign a unique variable name for each live range n Similar techniques used in register allocation to be covered next week. n n Option 2: simply remove all Ф functions n Every optimization in SSA needs to guarantee not to generate overlapping live ranges Stanford University CS 243 Winter 2006 35

Reference n “Efficient Computing Static Single Assignment Form and the Control Dependence Graph”, R. Cytron, J. Ferrante, B. Rosen, M. Wegman, and F. K. Zadeck, Transactions on Programming Languages and Systems (TOPLAS), Oct 1991. http: //citeseer. ist. psu. edu/cytron 91 effici ently. html Stanford University CS 243 Winter 2006 36

Backup Stanford University CS 243 Winter 2006 37

Handling Arrays n Difficult to treat A[i] as a variable = A[i] A[j] = V = A[k] n = R(A, i) A = W(A, j, V) = R(A, k) = R(A 8, i 7) A 9 = W(A 8, j 6, V 5) = R(A 9, k 4) The entire array can be treated like a scalar. Stanford University CS 243 Winter 2006 38

Unnecessary Liveness n W operator may introduce unnecessary liveness for A. Introduce HW (Hidden. W). repeat A[i] = i i = i +1 until i>10 Stanford University repeat i 2 = Ф(i 1, i 3) A 1 = Ф(A 0, A 2) A 2= W(A 1, i 2) i 3 = i 2 +1 until i 3>10 CS 243 Winter 2006 repeat i 2 = Ф(i 1, i 3) A 2= HW(i 2, i 2) i 3 = i 2 +1 until i 3>10 39