SRF Operation Issues for CEPC with Bunch Trains

SRF Operation Issues for CEPC with Bunch Trains Jiyuan Zhai IHEP CEPC-Spp. C Study Group Meeting Sept. 11, 2015, IHEP, Beijing

Content SRF cavity beam loading, HOM power and instability issues for different CEPC lattice scheme and operation energy: Pretzel (PZ) Scheme • Higgs (pre-CDR) • Super Z (with wiggler, H. P. Geng) • Super Z (bunch trains, U. Wienands) Local Double Ring (LDR or bunch train) Scheme • Higgs (J. Gao, M. Xiao) • Super Z (J. Gao, M. Xiao)
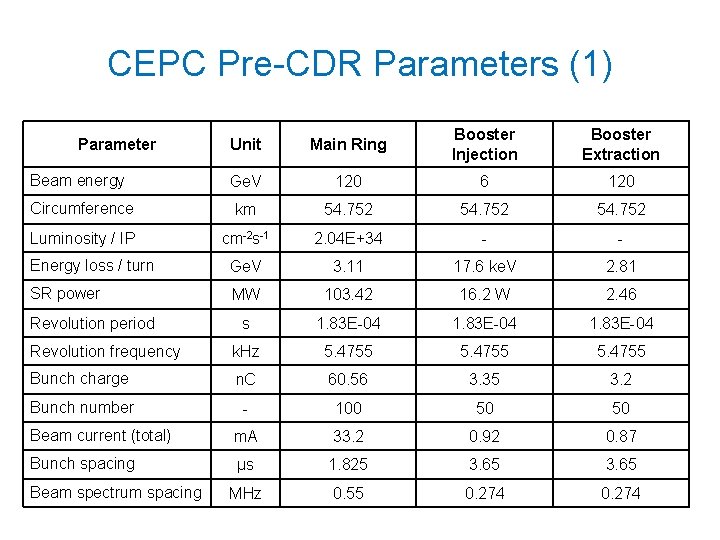
CEPC Pre-CDR Parameters (1) Unit Main Ring Booster Injection Booster Extraction Beam energy Ge. V 120 6 120 Circumference km 54. 752 Luminosity / IP cm-2 s-1 2. 04 E+34 - - Energy loss / turn Ge. V 3. 11 17. 6 ke. V 2. 81 SR power MW 103. 42 16. 2 W 2. 46 s 1. 83 E-04 Revolution frequency k. Hz 5. 4755 Bunch charge n. C 60. 56 3. 35 3. 2 Bunch number - 100 50 50 Beam current (total) m. A 33. 2 0. 92 0. 87 Bunch spacing μs 1. 825 3. 65 MHz 0. 55 0. 274 Parameter Revolution period Beam spectrum spacing
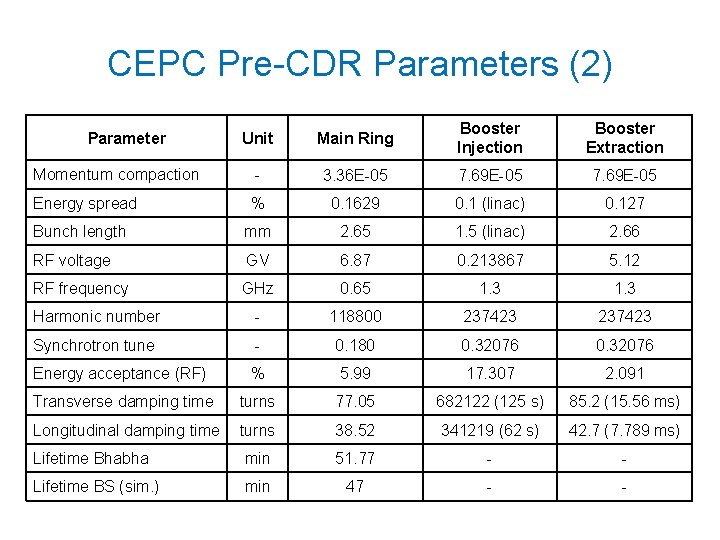
CEPC Pre-CDR Parameters (2) Unit Main Ring Booster Injection Booster Extraction Momentum compaction - 3. 36 E-05 7. 69 E-05 Energy spread % 0. 1629 0. 1 (linac) 0. 127 Bunch length mm 2. 65 1. 5 (linac) 2. 66 RF voltage GV 6. 87 0. 213867 5. 12 RF frequency GHz 0. 65 1. 3 Harmonic number - 118800 237423 Synchrotron tune - 0. 180 0. 32076 Energy acceptance (RF) % 5. 99 17. 307 2. 091 Transverse damping time turns 77. 05 682122 (125 s) 85. 2 (15. 56 ms) Longitudinal damping time turns 38. 52 341219 (62 s) 42. 7 (7. 789 ms) Lifetime Bhabha min 51. 77 - - Lifetime BS (sim. ) min 47 - - Parameter
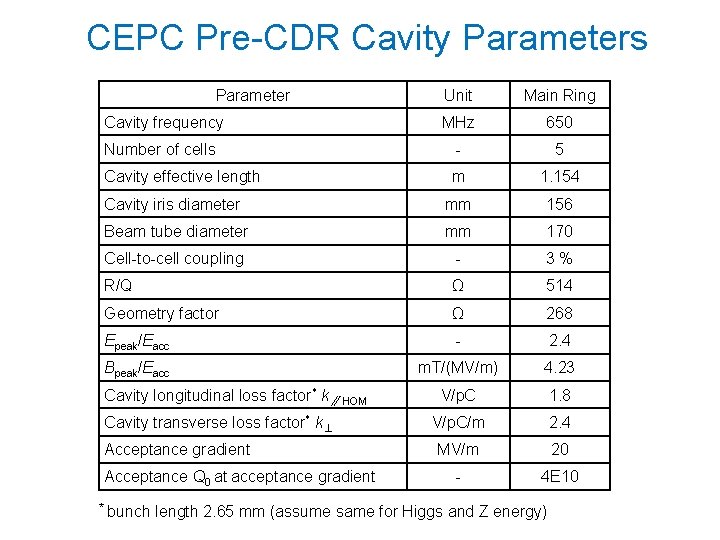
CEPC Pre-CDR Cavity Parameters Parameter Unit Main Ring Cavity frequency MHz 650 Number of cells - 5 Cavity effective length m 1. 154 Cavity iris diameter mm 156 Beam tube diameter mm 170 Cell-to-cell coupling - 3 % R/Q Ω 514 Geometry factor Ω 268 Epeak/Eacc - 2. 4 Bpeak/Eacc m. T/(MV/m) 4. 23 V/p. C 1. 8 V/p. C/m 2. 4 MV/m 20 - 4 E 10 Cavity longitudinal loss factor* k∥ HOM Cavity transverse loss factor* k⊥ Acceptance gradient Acceptance Q 0 at acceptance gradient * bunch length 2. 65 mm (assume same for Higgs and Z energy)
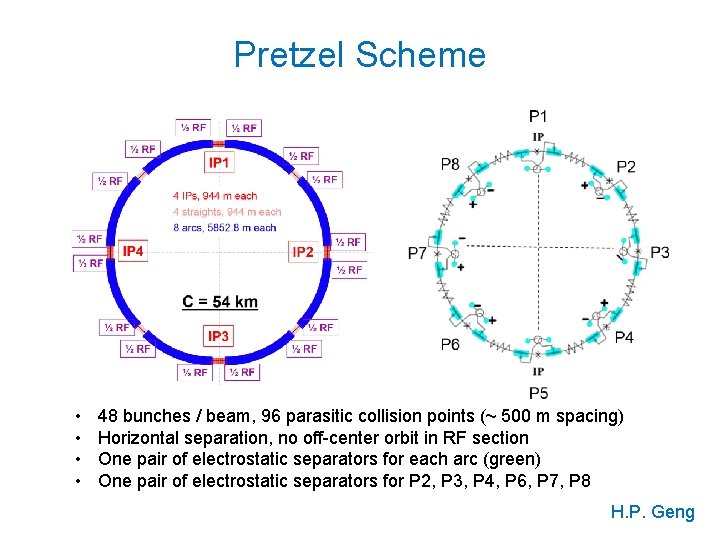
Pretzel Scheme • • 48 bunches / beam, 96 parasitic collision points (~ 500 m spacing) Horizontal separation, no off-center orbit in RF section One pair of electrostatic separators for each arc (green) One pair of electrostatic separators for P 2, P 3, P 4, P 6, P 7, P 8 H. P. Geng
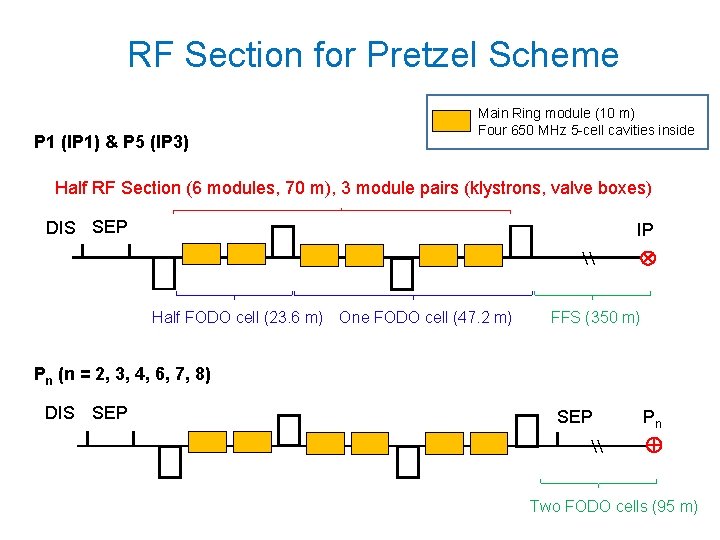
RF Section for Pretzel Scheme P 1 (IP 1) & P 5 (IP 3) Main Ring module (10 m) Four 650 MHz 5 -cell cavities inside Half RF Section (6 modules, 70 m), 3 module pairs (klystrons, valve boxes) DIS SEP IP \ Half FODO cell (23. 6 m) One FODO cell (47. 2 m) FFS (350 m) Pn (n = 2, 3, 4, 6, 7, 8) DIS SEP Pn \ Two FODO cells (95 m)
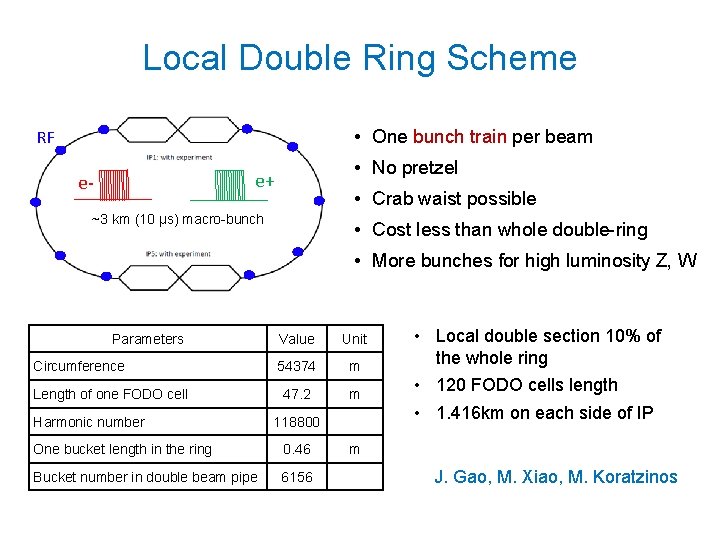
Local Double Ring Scheme • One bunch train per beam RF • No pretzel e+ e- • Crab waist possible ~3 km (10 μs) macro-bunch • Cost less than whole double-ring • More bunches for high luminosity Z, W Parameters Value Unit 54374 m 47. 2 m 118800 One bucket length in the ring 0. 46 m Bucket number in double beam pipe 6156 Circumference Length of one FODO cell Harmonic number • Local double section 10% of the whole ring • 120 FODO cells length • 1. 416 km on each side of IP J. Gao, M. Xiao, M. Koratzinos
![LDR Time Structure Parameters Z W H Beam energy [Ge. V] 45 80 120 LDR Time Structure Parameters Z W H Beam energy [Ge. V] 45 80 120](http://slidetodoc.com/presentation_image_h/37f58183912cf01f29d2543c42819542/image-9.jpg)
LDR Time Structure Parameters Z W H Beam energy [Ge. V] 45 80 120 Synchrotron radiation power per beam [MW] 50 50 50 SR loss/turn U 0 [Ge. V] 0. 062 0. 6 3. 01 Beam current I [m. A] 796. 8 84. 03 16. 62 Bunch population Ne [1011] 3. 09 3. 65 3. 61 Bunch number 2688 240 48 2 25 128 Distance between bunches [m] 0. 92 11. 5 58. 88 Bunch space time [ns] 3. 1 38. 3 196. 3 Bucket interval per bunch J. Gao, M. Xiao
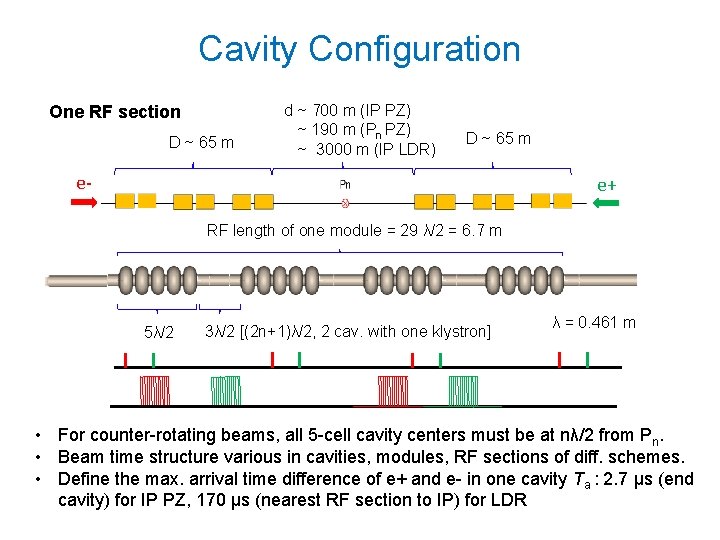
Cavity Configuration One RF section D ~ 65 m d ~ 700 m (IP PZ) ~ 190 m (Pn PZ) ~ 3000 m (IP LDR) D ~ 65 m e- e+ RF length of one module = 29 λ/2 = 6. 7 m 5λ/2 3λ/2 [(2 n+1)λ/2, 2 cav. with one klystron] λ = 0. 461 m • For counter-rotating beams, all 5 -cell cavity centers must be at nλ/2 from Pn. • Beam time structure various in cavities, modules, RF sections of diff. schemes. • Define the max. arrival time difference of e+ and e- in one cavity Ta : 2. 7 μs (end cavity) for IP PZ, 170 μs (nearest RF section to IP) for LDR

Parasitic Loss and Beam Loading • Tb : bunch spacing Td = 2 QL/ωn cavity filling time Assume incoherent HOM excitation, average Fr = ½, same as single pass excitation. P. B. Wilson, SLAC-PUB-6062 Equally-spaced bunches will have steady beam loading for fundamental mode. Cavity detuning for compensation.
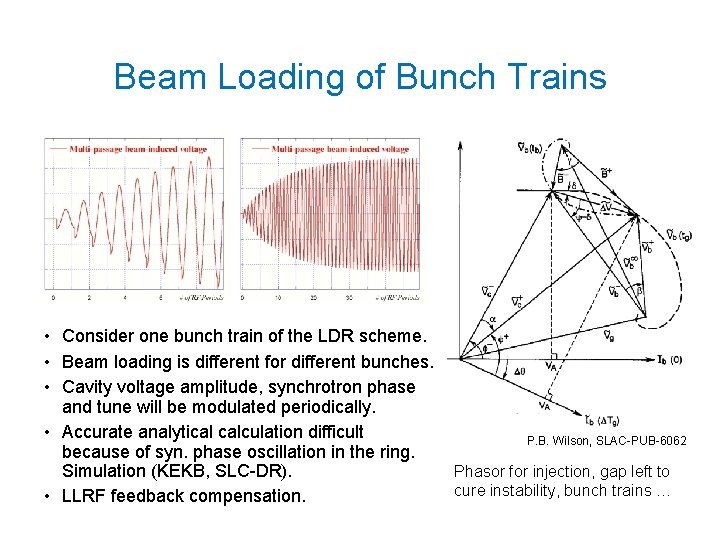
Beam Loading of Bunch Trains • Consider one bunch train of the LDR scheme. • Beam loading is different for different bunches. • Cavity voltage amplitude, synchrotron phase and tune will be modulated periodically. • Accurate analytical calculation difficult P. B. Wilson, SLAC-PUB-6062 because of syn. phase oscillation in the ring. Simulation (KEKB, SLC-DR). Phasor for injection, gap left to cure instability, bunch trains … • LLRF feedback compensation.

Beam Loading of Bunch Trains Rough estimation for H-LDR: Tb-train = 0. 2 μs, Ttrain = 10 μs, Tg = 183 us, Td = 1077 us. Tb-train and Ttrain << Td, the bunch train can be treated as a macro-bunch. Tg << Td, the beam induced voltage is same as the equal-spacing, thus the same average beam loading. Phase difference between the head and tail bunches: 10 deg Voltage difference between the head and tail bunches: 2. 8 MV D. Boussard, CERN SL / 91 -16

HOM Power and Coupled Bunch Instability • HOM power 10 ~ 50 times higher for HL-Z than H • CBI threshold ~ 1000 times lower for HL-Z (feedback not easy due to small bunch spacing) than H • Beam instabilities for bunch train • Bunch train beam spectrum and HOM spectrum relation.

HOM of Bunch Train for Higgs Run • HOM damping time limit between the nb bunches in a bunch train is ~ 50 times lower than the pretzel scheme (beam instability to be studied). • Average HOM power same with pretzel scheme. • Positive coherent HOM vector superposition could happen rather than simply adding their power. • According to LEP 2 bunch train measurement [CERN SL/94 -95], the HOM power enhancement factor is nb^(1/2) (assume no HOM coherence between two counter-rotating beams, but could happen). HOM coupler power handling capacity should have enough margin.
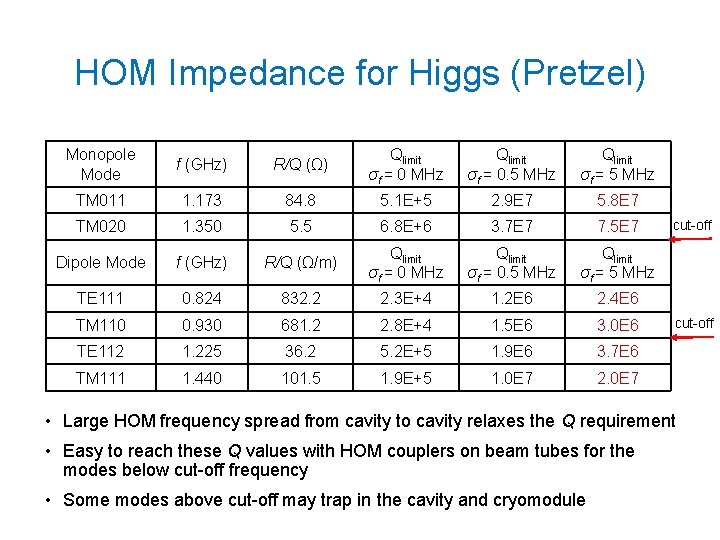
HOM Impedance for Higgs (Pretzel) Monopole Mode f (GHz) R/Q (Ω) Qlimit σf = 0 MHz Qlimit σf = 0. 5 MHz Qlimit σf = 5 MHz TM 011 1. 173 84. 8 5. 1 E+5 2. 9 E 7 5. 8 E 7 TM 020 1. 350 5. 5 6. 8 E+6 3. 7 E 7 7. 5 E 7 Dipole Mode f (GHz) R/Q (Ω/m) Qlimit σf = 0 MHz Qlimit σf = 0. 5 MHz Qlimit σf = 5 MHz TE 111 0. 824 832. 2 2. 3 E+4 1. 2 E 6 2. 4 E 6 TM 110 0. 930 681. 2 2. 8 E+4 1. 5 E 6 3. 0 E 6 TE 112 1. 225 36. 2 5. 2 E+5 1. 9 E 6 3. 7 E 6 TM 111 1. 440 101. 5 1. 9 E+5 1. 0 E 7 2. 0 E 7 cut-off • Large HOM frequency spread from cavity to cavity relaxes the Q requirement • Easy to reach these Q values with HOM couplers on beam tubes for the modes below cut-off frequency • Some modes above cut-off may trap in the cavity and cryomodule

Coherence of Counter-Rotating Beams Generally no coupling of counter-rotating bunches in the ring because of rapid distance change (average to zero). But coherence may happen in the cavity (depends on cavity position and modes symmetry). δ Vb 2 V 2+ Vb 1 V 2 - V 1+ V 1 - δ θ-δ Beam induced voltage is decided by the charge, not moving direction, Therefore, V 1+ = V 2 - , V 2+ = V 1 - , δ = 2π Ta / Tn , θ = 2π Tb / Tn We have therefore, For the case Ta << Tb , K = 1/2 by averaging the first cosine term. Thus, twice the single beam loss.
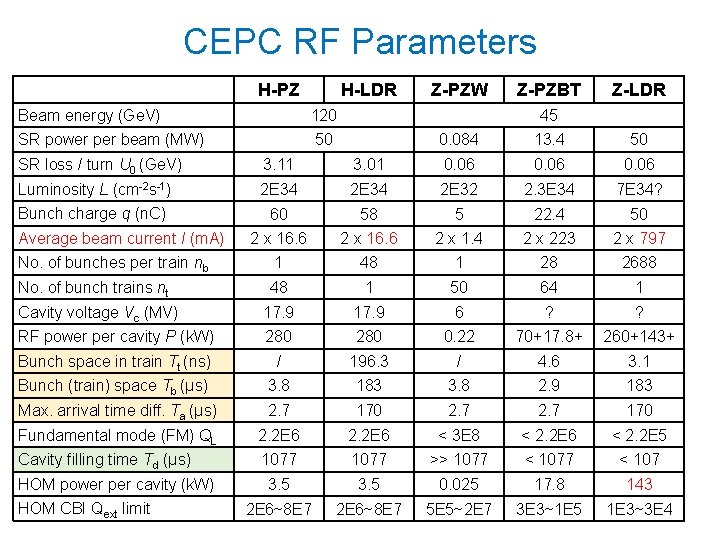
CEPC RF Parameters H-PZ H-LDR Beam energy (Ge. V) 120 SR power per beam (MW) 50 Z-PZW Z-PZBT Z-LDR 45 0. 084 13. 4 50 SR loss / turn U 0 (Ge. V) 3. 11 3. 01 0. 06 Luminosity L (cm-2 s-1) 2 E 34 2 E 32 2. 3 E 34 7 E 34? Bunch charge q (n. C) 60 58 5 22. 4 50 2 x 16. 6 2 x 1. 4 2 x 223 2 x 797 No. of bunches per train nb 1 48 1 28 2688 No. of bunch trains nt 48 1 50 64 1 Cavity voltage Vc (MV) 17. 9 6 ? ? RF power per cavity P (k. W) 280 0. 22 70+17. 8+ 260+143+ Bunch space in train Tt (ns) / 196. 3 / 4. 6 3. 1 Bunch (train) space Tb (μs) 3. 8 183 3. 8 2. 9 183 Max. arrival time diff. Ta (μs) 2. 7 170 Fundamental mode (FM) QL 2. 2 E 6 < 3 E 8 < 2. 2 E 6 < 2. 2 E 5 Cavity filling time Td (μs) 1077 >> 1077 < 107 3. 5 0. 025 17. 8 143 2 E 6~8 E 7 5 E 5~2 E 7 3 E 3~1 E 5 1 E 3~3 E 4 Average beam current I (m. A) HOM power per cavity (k. W) HOM CBI Qext limit

High Current Super Z Operation • HOMs power will be a major issue for running at the Z pole. Reduce the cavity frequency, reduce cell number, reduce cavity number in one module, SRF staging (as FCC-ee) • Large detuning (larger than the revolution frequency), longitudinal coupled-bunch mode instability, feedback • Robison instability, direct feed back (like BEPCII) • Many other beam dynamics and hardware issues related to bunch train operation • Z-pole design should be compromised with well-defined boundary conditions (machine layout, luminosity, beam dynamics, SRF)

Summary • CEPC beam loading, HOM power and multi-bunch instabilities are related to beam time structure & cavity configuration in the ring. • Pre-CDR SRF design is suitable for Higgs run of the Local Double Ring (Bunch Train) scheme. Transient beam loading could be compensated by LLRF feedback. Details to be studied. • Coherence of two counter-rotating beams have (trivial? ) effect on the beam loading and HOMs. • Pre-CDR cavity can’t be used for high luminosity (hyper) Z run. Need inputs from physics requirement.

Back up
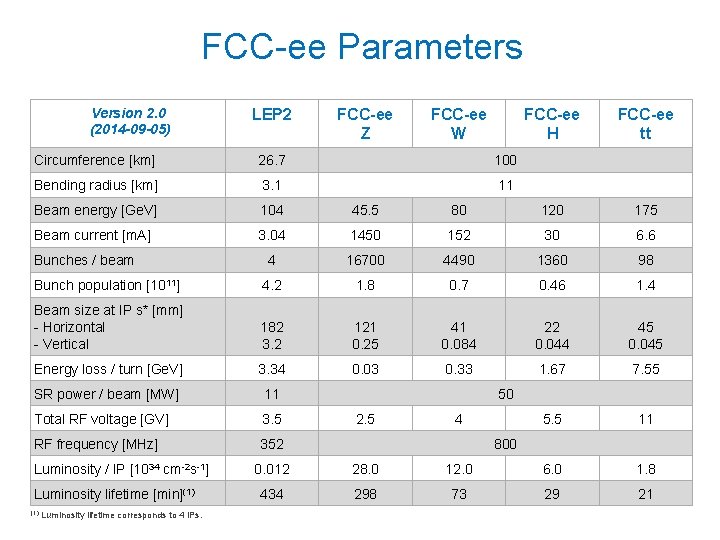
FCC-ee Parameters Version 2. 0 (2014 -09 -05) LEP 2 FCC-ee Z FCC-ee W FCC-ee H FCC-ee tt Circumference [km] 26. 7 100 Bending radius [km] 3. 1 11 Beam energy [Ge. V] 104 45. 5 80 120 175 Beam current [m. A] 3. 04 1450 152 30 6. 6 4 16700 4490 1360 98 Bunch population [1011] 4. 2 1. 8 0. 7 0. 46 1. 4 Beam size at IP s* [mm] - Horizontal - Vertical 182 3. 2 121 0. 25 41 0. 084 22 0. 044 45 0. 045 Energy loss / turn [Ge. V] 3. 34 0. 03 0. 33 1. 67 7. 55 SR power / beam [MW] 11 Total RF voltage [GV] 3. 5 5. 5 11 RF frequency [MHz] 352 Bunches / beam Luminosity / IP [1034 cm-2 s-1] Luminosity lifetime [min](1) Luminosity lifetime corresponds to 4 IPs. 50 2. 5 4 800 0. 012 28. 0 12. 0 6. 0 1. 8 434 298 73 29 21
- Slides: 22