SR Pertenencia SR4 Prof Jos Juan Aliaga Maraver

SR: Pertenencia SR_4 Prof. José Juan Aliaga Maraver Expresión gráfica

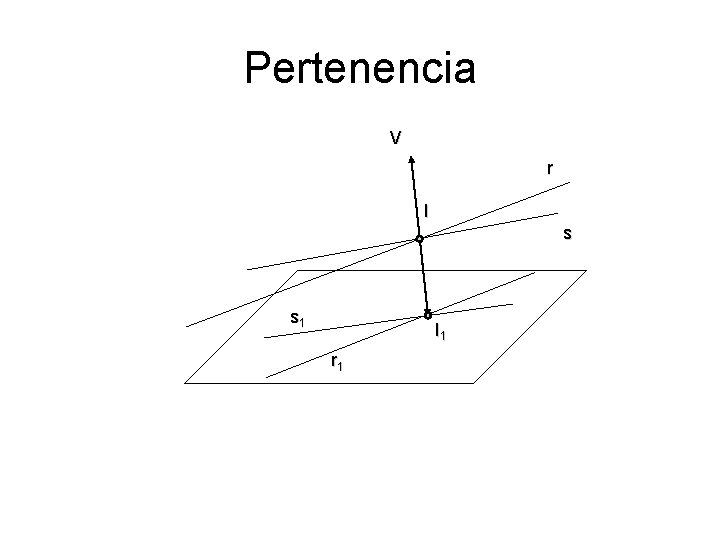
Pertenencia V r I s s 1 I 1 r 1

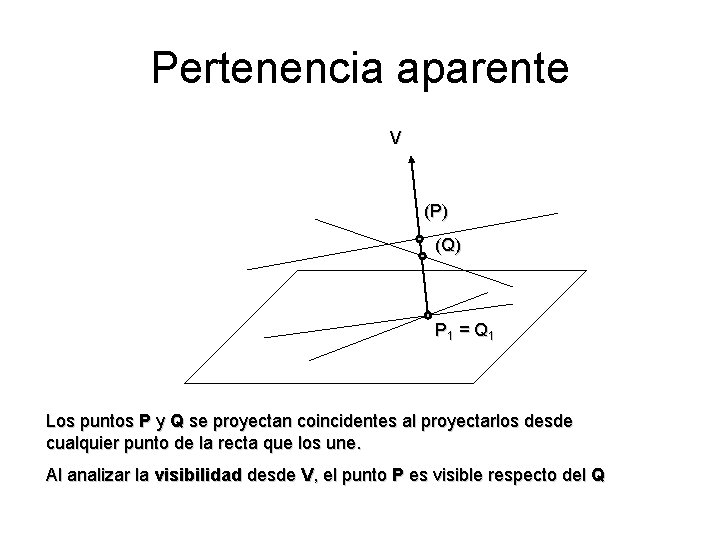
Pertenencia aparente V (P) (Q) P 1 = Q 1 Los puntos P y Q se proyectan coincidentes al proyectarlos desde cualquier punto de la recta que los une. Al analizar la visibilidad desde V, el punto P es visible respecto del Q

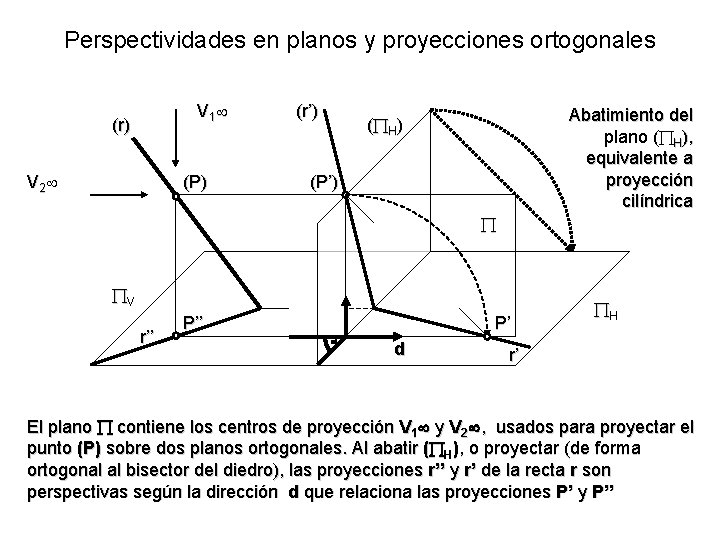
Perspectividades en planos y proyecciones ortogonales V 1 (r) V 2 (P) (r’) Abatimiento del plano ( H), equivalente a proyección cilíndrica ( H ) (P’) V r’’ P’ d H r’ El plano contiene los centros de proyección V 1 y V 2 , usados para proyectar el punto (P) sobre dos planos ortogonales. Al abatir ( H), o proyectar (de forma ortogonal al bisector del diedro), las proyecciones r’’ y r’ de la recta r son perspectivas según la dirección d que relaciona las proyecciones P’ y P’’

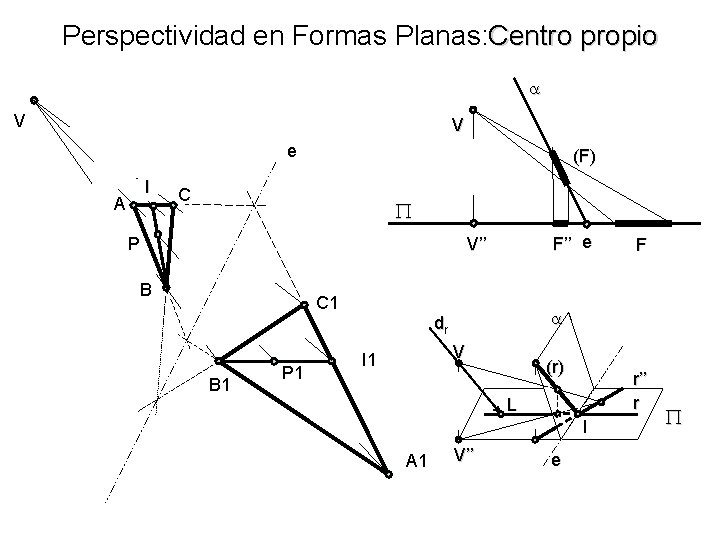
Perspectividad en Formas Planas: Centro propio V V e I A (F) C P F’’ e V’’ B C 1 B 1 P 1 dr V I 1 (r) r’’ r L I A 1 F V’’ e

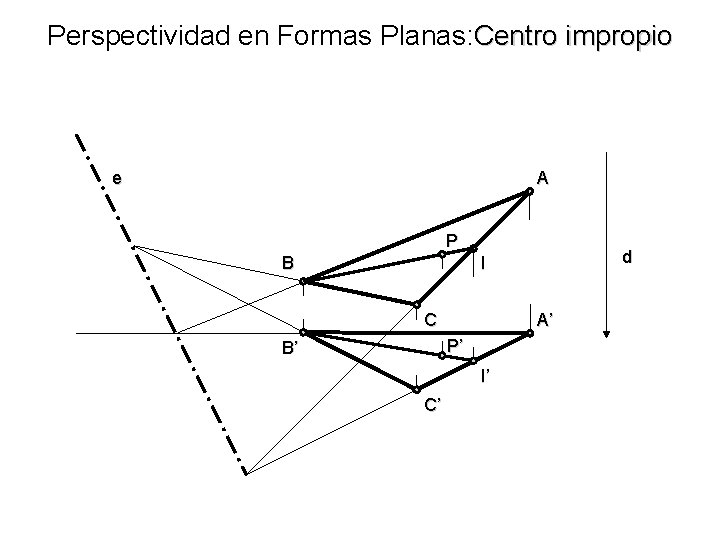
Perspectividad en Formas Planas: Centro impropio e A P B d I C A’ P’ B’ I’ C’

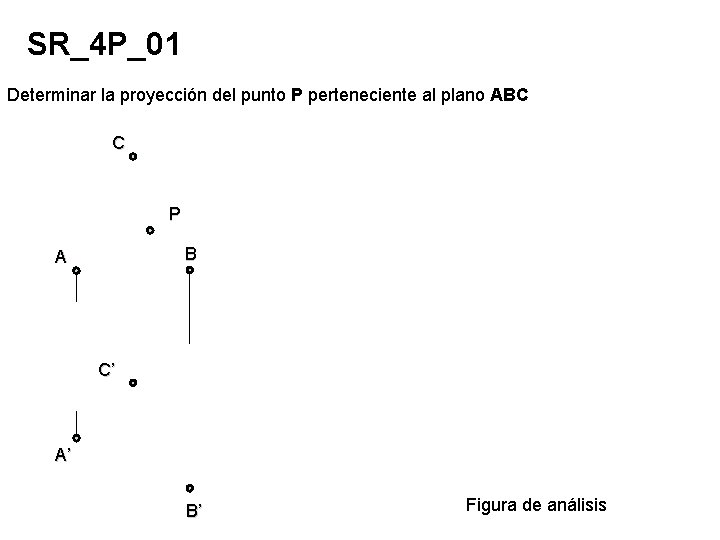
SR_4 P_01 Determinar la proyección del punto P perteneciente al plano ABC C P B A C’ A’ B’ Figura de análisis

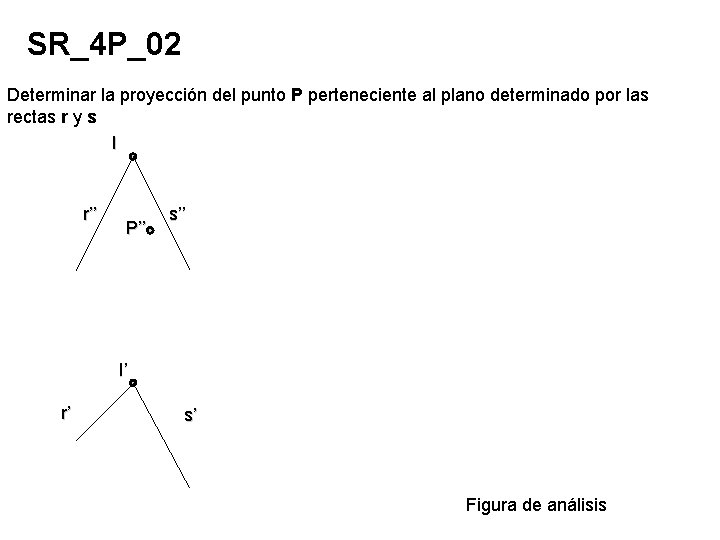
SR_4 P_02 Determinar la proyección del punto P perteneciente al plano determinado por las rectas r y s I r’’ P’’ s’’ I’ r’ s’ Figura de análisis

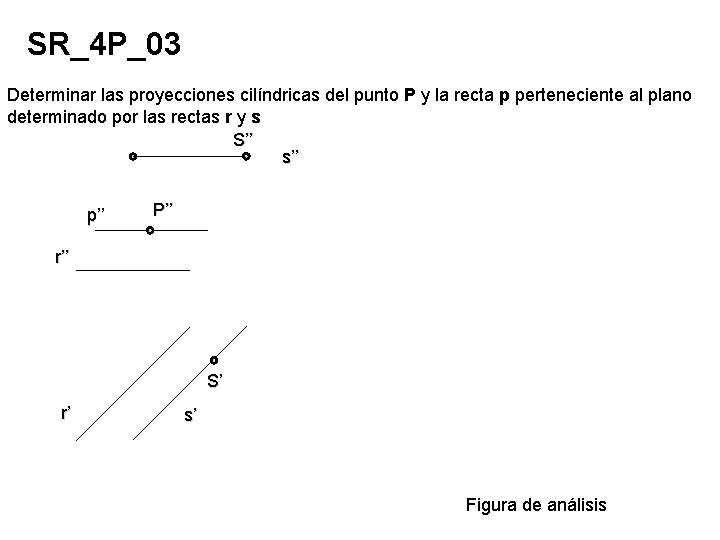
SR_4 P_03 Determinar las proyecciones cilíndricas del punto P y la recta p perteneciente al plano determinado por las rectas r y s S’’ s’’ p’’ P’’ r’’ S’ r’ s’ Figura de análisis

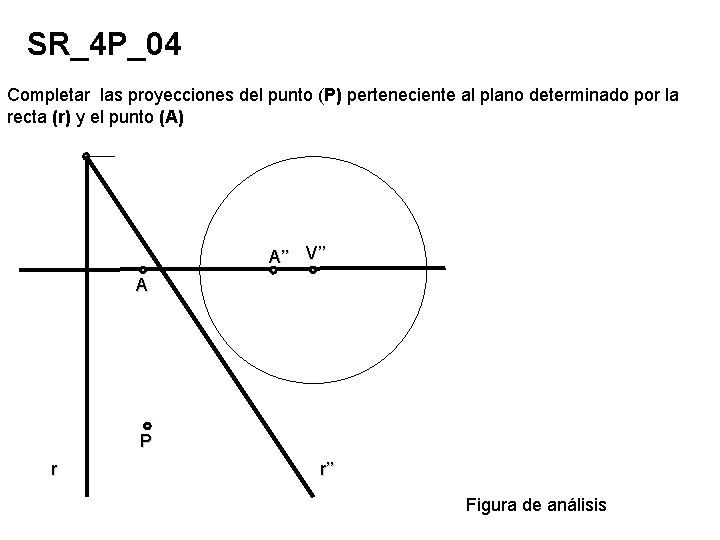
SR_4 P_04 Completar las proyecciones del punto (P) perteneciente al plano determinado por la recta (r) y el punto (A) A’’ V’’ A P r r’’ Figura de análisis

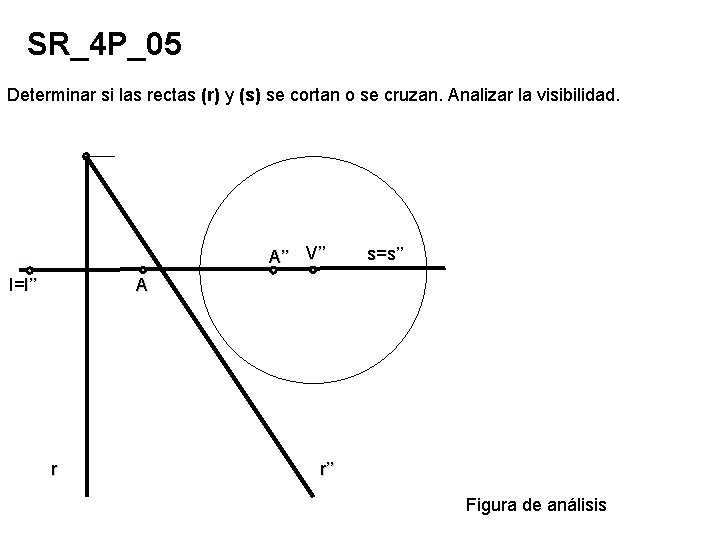
SR_4 P_05 Determinar si las rectas (r) y (s) se cortan o se cruzan. Analizar la visibilidad. A’’ V’’ I=I’’ s=s’’ A r r’’ Figura de análisis

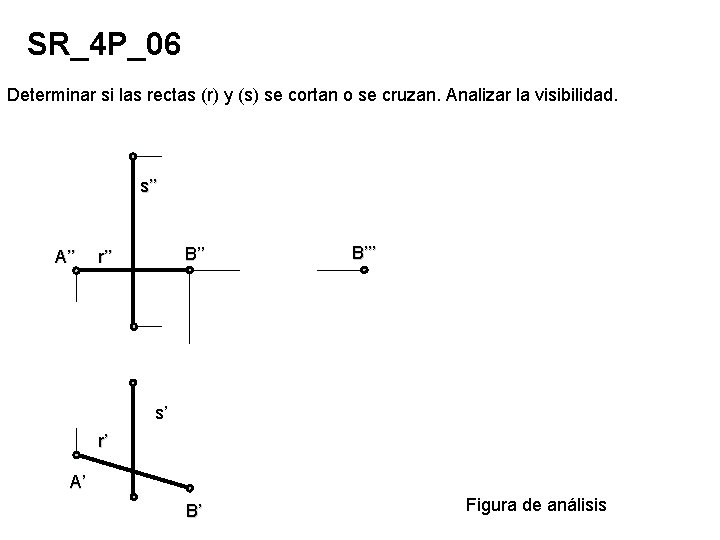
SR_4 P_06 Determinar si las rectas (r) y (s) se cortan o se cruzan. Analizar la visibilidad. s’’ A’’ B’’ r’’ B’’’ s’ r’ A’ B’ Figura de análisis

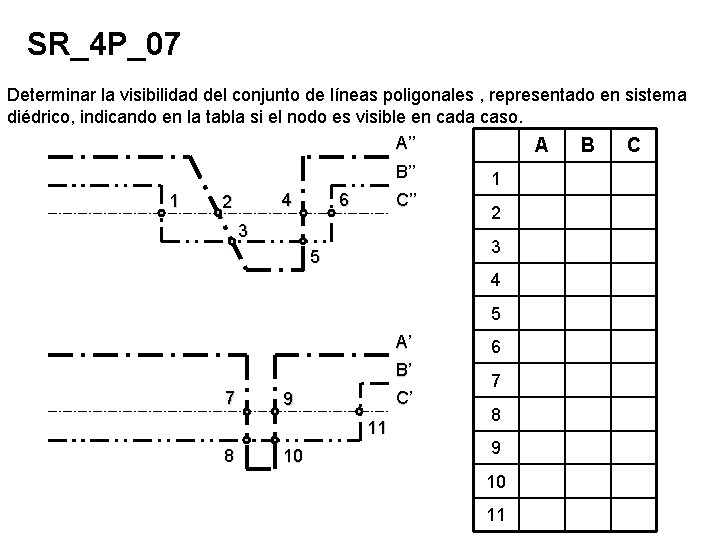
SR_4 P_07 Determinar la visibilidad del conjunto de líneas poligonales , representado en sistema diédrico, indicando en la tabla si el nodo es visible en cada caso. A’’ A B C B’’ 1 4 2 6 C’’ 3 1 2 3 5 4 5 A’ B’ 7 C’ 9 11 8 10 6 7 8 9 10 11