Square Roots and Irrational Numbers LESSON 8 6

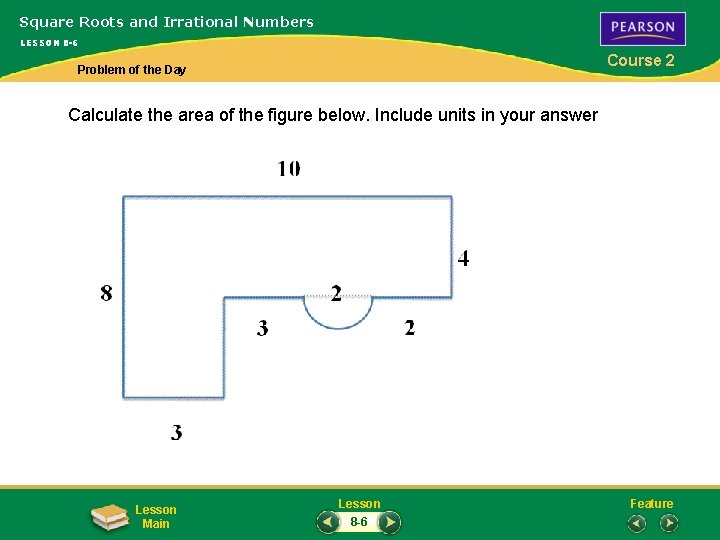
Square Roots and Irrational Numbers LESSON 8 -6 Course 2 Problem of the Day Calculate the area of the figure below. Include units in your answer Lesson Main Lesson 8 -6 Feature

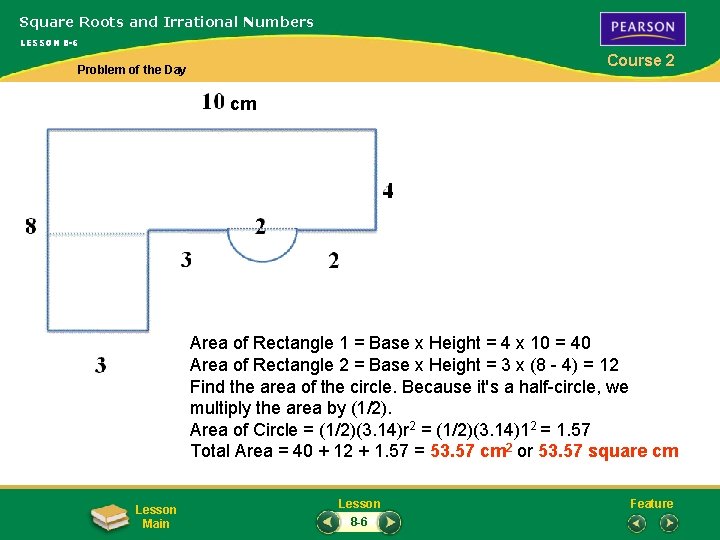
Square Roots and Irrational Numbers LESSON 8 -6 Course 2 Problem of the Day cm Area of Rectangle 1 = Base x Height = 4 x 10 = 40 Area of Rectangle 2 = Base x Height = 3 x (8 - 4) = 12 Find the area of the circle. Because it's a half-circle, we multiply the area by (1/2). Area of Circle = (1/2)(3. 14)r 2 = (1/2)(3. 14)12 = 1. 57 Total Area = 40 + 12 + 1. 57 = 53. 57 cm 2 or 53. 57 square cm Lesson Main Lesson 8 -6 Feature

Square Roots and Irrational Numbers LESSON 8 -6 Course 2 Check Skills You’ll Need (For help, go to Lesson 2 -1. ) 1. Vocabulary Review How do you find the square of a number? Simplify. 2. 82 3. 122 4. 22 5. 72 Check Skills You’ll Need Lesson Main Lesson 8 -6 Feature

Square Roots and Irrational Numbers LESSON 8 -6 Course 2 Check Skills You’ll Need Solutions 1. Multiply the number by itself. 2. 82 = 8 • 8 = 64 3. 122 = 12 • 12 = 144 4. 22 = 2 • 2 = 4 5. 72 = 7 • 7 = 49 Lesson Main Lesson 8 -6 Feature

Course 2 Perfect square: a number that is a square of an integer (Integer: positive whole numbers, their opposites, and zero) 82 = 8 • 8 = 64; so 64 is a perfect square The inverse of squaring a number is finding a square root. 82 = 64 Lesson Main Lesson Feature

Square Roots and Irrational Numbers LESSON 8 -6 Course 2 Additional Examples Simplify 81 = 9 81. 81 = 92 Quick Check Lesson Main Lesson 8 -6 Feature

Square Roots and Irrational Numbers LESSON 8 -6 Course 2 Additional Examples Estimate the value of 49 < 7 < 60 < 64 60 < 8 60. Find perfect squares close to 60. Simplify. 60 is between 7 and 8. Since 60 is closer to 64 than it is to 49, 60 8. Quick Check Lesson Main Lesson 8 -6 Feature

Course 2 Rational number: a number that can be written as a fraction (ratio of two integers) Irrational number: a number that cannot be written as a fraction. If it’s written as a decimal, it does not terminate nor does it repeat. Lesson Main Lesson Feature

Course 2 If a positive integer is not a perfect square, its square root is irrational. Rational Irrational Lesson Main Lesson Feature

Square Roots and Irrational Numbers LESSON 8 -6 Course 2 Additional Examples Identify each number as rational or irrational. a. 121 rational 121 is a perfect square. b. 30 irrational 30 is not a perfect square. c. – 0. 5167 rational It is a terminating decimal. d. 2992999. . . irrational The decimal neither terminates nor repeats. Quick Check Lesson Main Lesson 8 -6 Feature

Square Roots and Irrational Numbers LESSON 8 -6 Course 2 Lesson Quiz Estimate each square root. 1. 6 2. about 2 22 about 5 Identify each as rational or irrational. 3. 0. 625 4. rational Lesson Main 150 irrational Lesson 8 -6 Feature

Course 2 Homework: Bring your 3 -D object, ruler, scissors Lesson 8 -6, pp. 402 -403, #s 1 -38, all Lesson Main Lesson Feature