Square Differences Some numbers can be written as

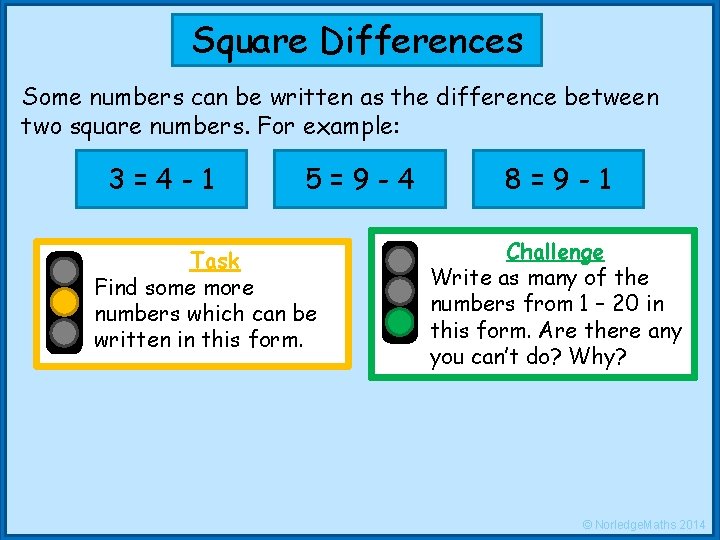
Square Differences Some numbers can be written as the difference between two square numbers. For example: 3=4 -1 5=9 -4 Task Find some more numbers which can be written in this form. 8=9 -1 Challenge Write as many of the numbers from 1 – 20 in this form. Are there any you can’t do? Why? © Norledge. Maths 2014

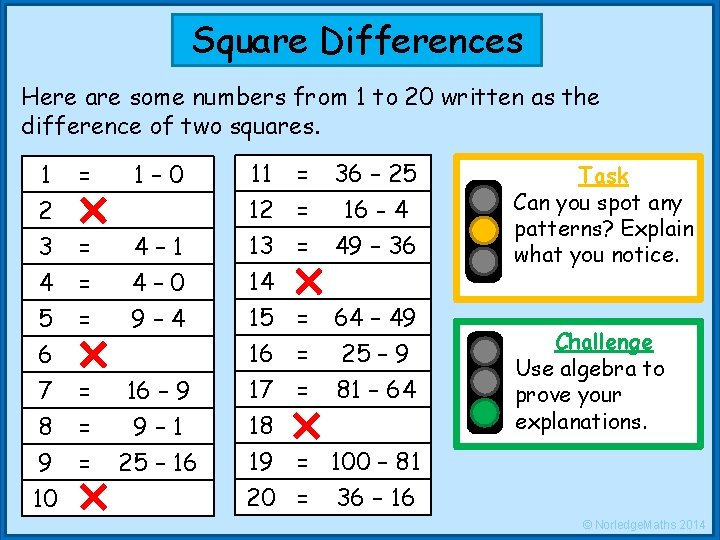
Square Differences Here are some numbers from 1 to 20 written as the difference of two squares. 1 2 3 4 = 1– 0 = = 4– 1 4– 0 5 6 7 8 9 10 = 9– 4 = = = 16 – 9 9– 1 25 – 16 11 = 12 = 13 = 14 36 – 25 16 - 4 49 – 36 15 16 17 18 19 20 64 – 49 25 – 9 81 – 64 = = = Task Can you spot any patterns? Explain what you notice. Challenge Use algebra to prove your explanations. = 100 – 81 = 36 – 16 © Norledge. Maths 2014

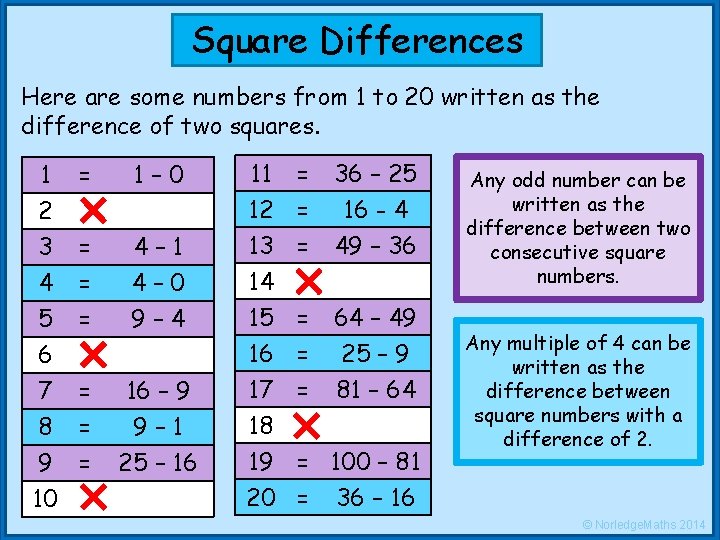
Square Differences Here are some numbers from 1 to 20 written as the difference of two squares. 1 2 3 4 = 1– 0 = = 4– 1 4– 0 5 6 7 8 9 10 = 9– 4 = = = 16 – 9 9– 1 25 – 16 11 = 12 = 13 = 14 36 – 25 16 - 4 49 – 36 15 16 17 18 19 20 64 – 49 25 – 9 81 – 64 = = 100 – 81 = 36 – 16 Any odd number can be written as the difference between two consecutive square numbers. Any multiple of 4 can be written as the difference between square numbers with a difference of 2. © Norledge. Maths 2014

Square Differences Can you prove these two results using algebra? The difference between two consecutive squares is odd. The difference between two square numbers with a difference of 2 is a multiple of 4. © Norledge. Maths 2014

Square Differences The difference between two consecutive squares is odd. Let n² = the first square number. The next square number = (n + 1)² - n² = n² + 2 n + 1 - n² = 2 n + 1 2 n is always even, so 2 n + 1 is odd. The difference between two square numbers with a difference of 2 is a multiple of 4. (n + 2)² - n² = n² + 4 n + 4 - n² = 4 n + 4 = 4(n + 1) is a multiple of 4. © Norledge. Maths 2014