SQL and Query Execution for Aggregation Reserves Example

SQL and Query Execution for Aggregation

Reserves Example Instances • Sailors Boats

Queries With GROUP BY • To generate values for a column based on groups of rows, use aggregate functions in SELECT statements with the GROUP BY clause SELECT [DISTINCT] target-list FROM relation-list [WHERE qualification] GROUP BY grouping-list • The target-list contains – (i) list of column names & – (ii) terms with aggregate operations (e. g. , MIN (S. age)). • column name list (i) can contain only attributes from the grouping-list.

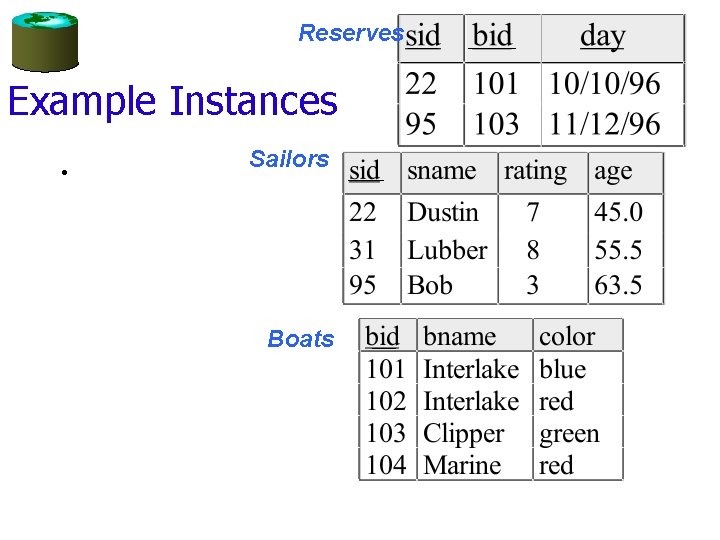
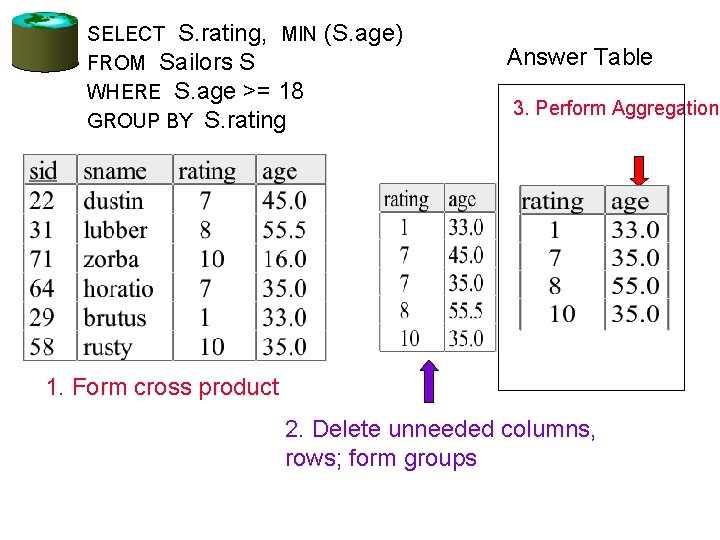
Group By Examples For each rating, find the average of the sailors SELECT S. rating, AVG • FROM Sailors S GROUP BY S. rating (S. age) For each rating find the age of the youngest sailor with age ≥ 18 SELECT S. rating, MIN FROM Sailors S WHERE S. age >= 18 GROUP BY S. rating (S. age)

Conceptual Evaluation SELECT [DISTINCT] target-list FROM relation-list [WHERE qualification] GROUP BY grouping-list • The cross-product of relation-list is computed, tuples that fail qualification are discarded, `unnecessary’ fields are deleted, and the remaining tuples are partitioned into groups by the value of attributes in grouping-list. • One answer tuple is generated per qualifying group. • If DISTINCT is specified: drop duplicate answer tuples.

SELECT S. rating, MIN FROM Sailors S WHERE S. age >= 18 GROUP BY S. rating (S. age) Answer Table 3. Perform Aggregation • 1. Form cross product 2. Delete unneeded columns, rows; form groups

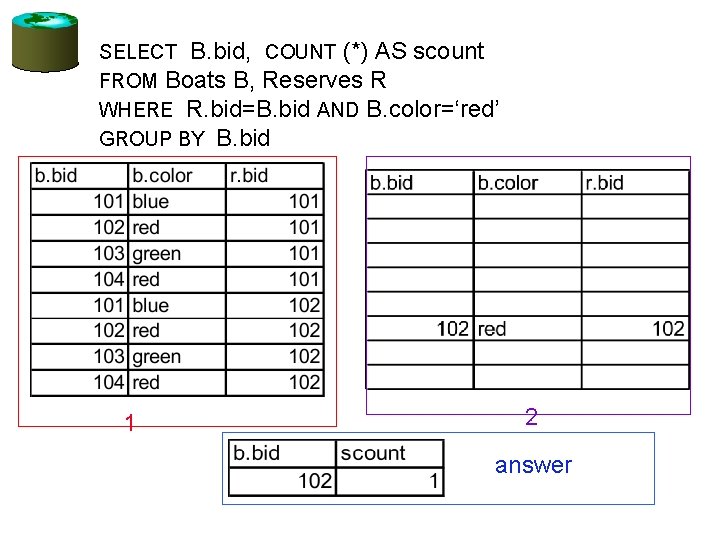
Find the number of reservations for each red boat. SELECT B. bid, COUNT(*) AS numres FROM Boats B, Reserves R WHERE R. bid=B. bid AND B. color=‘red’ GROUP BY B. bid • Grouping over a join of two relations.

SELECT B. bid, COUNT (*) AS scount FROM Boats B, Reserves R WHERE R. bid=B. bid AND B. color=‘red’ GROUP BY B. bid 1 2 answer

Queries With GROUP BY and HAVING SELECT [DISTINCT] target-list FROM relation-list WHERE qualification GROUP BY grouping-list HAVING group-qualification • Use the HAVING clause with the GROUP BY clause to restrict which group-rows are returned in the result set

Conceptual Evaluation • Form groups as before. • The group-qualification is then applied to eliminate some groups. • Expressions in group-qualification must have a single value per group! • That is, attributes in group-qualification must be arguments of an aggregate op or must also appear in the grouping-list. (SQL does not exploit primary key semantics here!) • One answer tuple is generated per qualifying group.

Find the age of the youngest sailor with age ≥ 18, for each rating with at least 2 such sailors SELECT S. rating, MIN (S. age) FROM Sailors S WHERE S. age >= 18 GROUP BY S. rating HAVING COUNT (*) > 1 2 3 Answer relation

Aggregate Sort GROUP BY: Naïve Solution Sort • • • The Sort iterator ensures that all tuples are output in sequence The Aggregate iterator keeps running info (“transition values”) on agg functions in the SELECT list, per group – E. g. , for COUNT, it keeps count-so-far – For SUM, it keeps sum-so-far – For AVERAGE it keeps sum-so-far and count-so-far As soon as the Aggregate iterator sees a tuple from a new group: – It produces an output for the old group based on the agg function • E. g. for AVERAGE it returns (sum-so-far/count-so-far) – It resets its running info. – It updates the running info with the new tuple’s info 12

An Alternative to Sorting: Hashing! • Idea: – Many of the things we use sort for don’t exploit the order of the sorted data – E. g. : forming groups in GROUP BY – E. g. : removing duplicates in DISTINCT • Often good enough to match all tuples with equal fieldvalues • Hashing does this! – And may be cheaper than sorting! (Hmmm…!) – But how to do it for data sets bigger than memory? ? 13

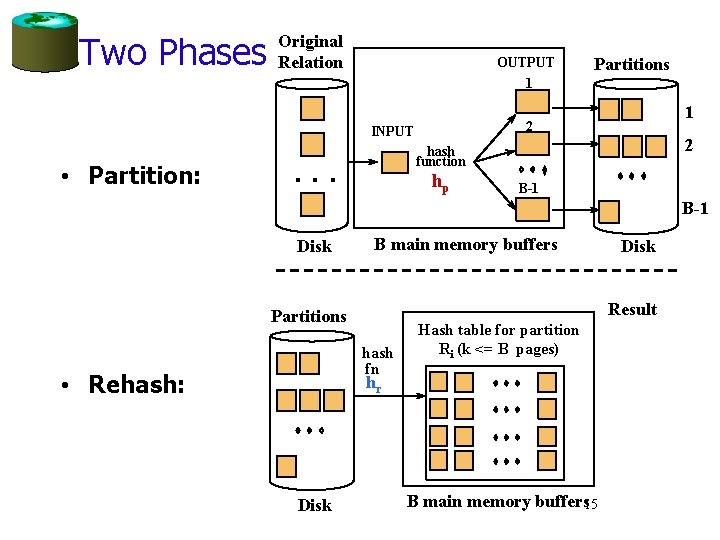
General Idea • Two phases: – Partition: use a hash function hp to split tuples into partitions on disk. • We know that all matches live in the same partition. • Partitions are “spilled” to disk via output buffers – Re. Hash: for each partition on disk, read it into memory and build a main-memory hash table based on a hash function hr • Then go through each bucket of this hash table to bring together matching tuples 14

Two Phases Original Relation OUTPUT 1 1 2 INPUT • Partition: Partitions 2 hash function . . . hp B-1 Disk B main memory buffers Result Partitions hash fn • Rehash: Hash table for partition Ri (k <= B pages) hr Disk B main memory buffers 15

Analysis • How big of a table can we hash in two passes? – B-1 “spill partitions” in Phase 1 – Each should be no more than B blocks big – Answer: B(B-1). • Said differently: We can hash a table of size N blocks in about space – Much like sorting! • Have a bigger table? Recursive partitioning! – In the Re. Hash phase, if a partition b is bigger than B, then recurse: • pretend that b is a table we need to hash, run the Partitioning phase on b, and then the Re. Hash phase on each of its (sub)partitions 16

Hash GROUP BY: Naïve Solution (similar to the Sort GROUPBY) Aggregate Hash • • • The Hash iterator permutes its input so that all tuples are output in groups The Aggregate iterator keeps running info (“transition values”) on agg functions in the SELECT list, per group – E. g. , for COUNT, it keeps count-so-far – For SUM, it keeps sum-so-far – For AVERAGE it keeps sum-so-far and count-so-far When the Aggregate iterator sees a tuple from a new group: 1. It produces an output for the old group based on the agg function • – – E. g. for AVERAGE it returns (sum-so-far/count-so-far) It resets its running info. It updates the running info with the new tuple’s info 17

We Can Do Better! • Hash. Agg Combine the summarization into the hashing process – During the Re. Hash phase, don’t store tuples, store pairs of the form <Group. Vals, Trans. Vals> – When we want to insert a new tuple into the hash table • If we find a matching Group. Vals, just update the Trans. Vals appropriately • Else insert a new <Group. Vals, Trans. Vals> pair • What’s the benefit? – Q: How many pairs will we have to handle? – A: Number of distinct values of Group. Vals columns • Not the number of tuples!! • – Also probably “narrower” than the tuples Can we play the same trick during sorting? 18

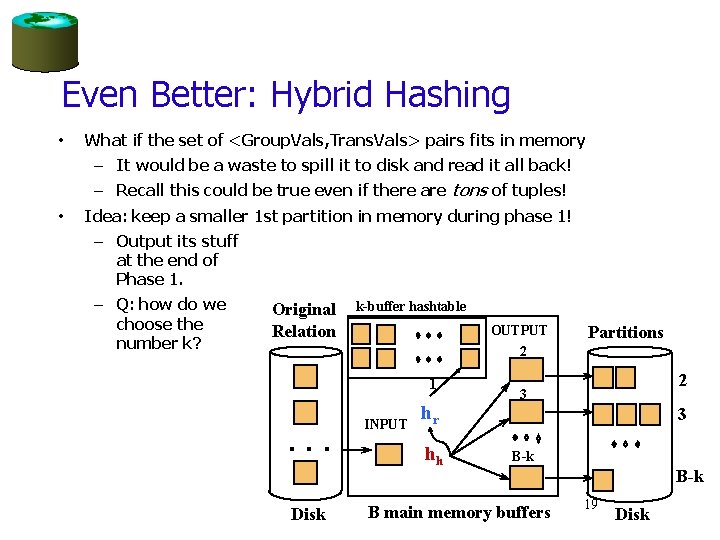
Even Better: Hybrid Hashing • What if the set of <Group. Vals, Trans. Vals> pairs fits in memory – It would be a waste to spill it to disk and read it all back! – Recall this could be true even if there are tons of tuples! • Idea: keep a smaller 1 st partition in memory during phase 1! – Output its stuff at the end of Phase 1. – Q: how do we choose the number k? Original Relation k-buffer hashtable OUTPUT 2 1 . . . Disk INPUT hr hh Partitions 2 3 3 B-k B main memory buffers B-k 19 Disk

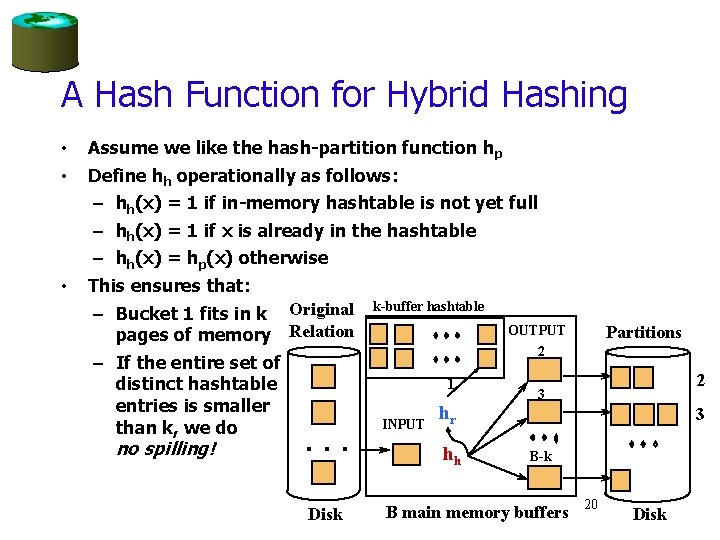
A Hash Function for Hybrid Hashing • • • Assume we like the hash-partition function hp Define hh operationally as follows: – hh(x) = 1 if in-memory hashtable is not yet full – hh(x) = 1 if x is already in the hashtable – hh(x) = hp(x) otherwise This ensures that: – Bucket 1 fits in k Original k-buffer hashtable OUTPUT pages of memory Relation 2 – If the entire set of 1 distinct hashtable 3 entries is smaller hr INPUT than k, we do no spilling! h B-k . . . Disk Partitions 2 3 h B main memory buffers 20 Disk