Spreadsheet Modeling Decision Analysis A Practical Introduction to

Spreadsheet Modeling & Decision Analysis A Practical Introduction to Management Science 5 th edition Cliff T. Ragsdale © 2007 South-Western College Publishing 1

Chapter 6 Integer Linear Programming © 2007 South-Western College Publishing 2

Introduction § When one or more variables in an LP problem must assume an integer value we have an Integer Linear Programming (ILP) problem. § ILPs occur frequently… – Scheduling workers – Manufacturing airplanes § Integer variables also allow us to build more accurate models for a number of common business problems. © 2007 South-Western College Publishing 3

Integrality Conditions MAX: 350 X 1 + 300 X 2 S. T. : 1 X 1 + 1 X 2 <= 200 9 X 1 + 6 X 2 <= 1566 12 X 1 + 16 X 2 <= 2880 X 1, X 2>= 0 X 1, X 2 must be integers } } } profit pumps labor tubing nonnegativity integrality Integrality conditions are easy to state but make the problem much more difficult (and sometimes impossible) to solve. © 2007 South-Western College Publishing 4

Relaxation § Original ILP MAX: S. T. : 2 X 1 + 3 X 2 <= 8. 25 2. 5 X 1 + X 2 <= 8. 75 X 1, X 2 >= 0 X 1, X 2 must be integers § LP Relaxation MAX: S. T. : 2 X 1 + 3 X 2 <= 8. 25 2. 5 X 1 + X 2 <= 8. 75 X 1, X 2 >= 0 © 2007 South-Western College Publishing 5

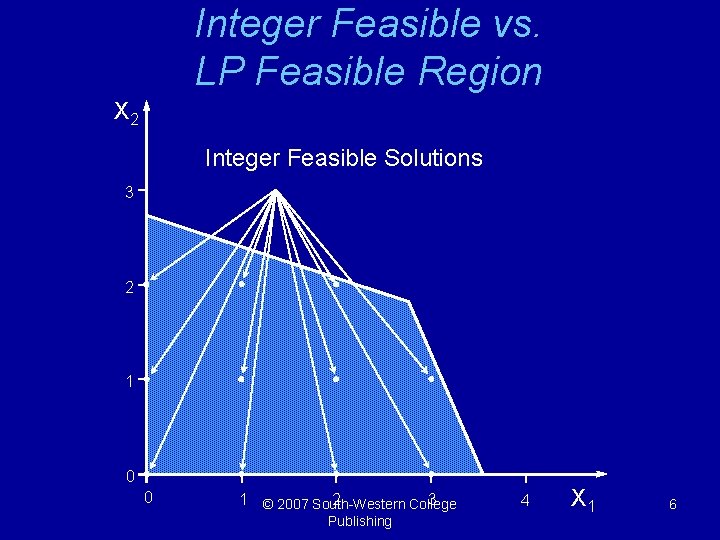
Integer Feasible vs. LP Feasible Region X 2 Integer Feasible Solutions 3 2 1 0 0 1 © 2007 South-Western 2 3 College Publishing 4 X 1 6

Solving ILP Problems § When solving an LP relaxation, sometimes you “get lucky” and obtain an integer feasible solution. § This was the case in the original Blue Ridge Hot Tubs problem in earlier chapters. § But what if we reduce the amount of labor available to 1520 hours and the amount of tubing to 2650 feet? See file Fig 6 -2. xls © 2007 South-Western College Publishing 7

Bounds § The optimal solution to an LP relaxation of an ILP problem gives us a bound on the optimal objective function value. § For maximization problems, the optimal relaxed objective function values is an upper bound on the optimal integer value. § For minimization problems, the optimal relaxed objective function values is a lower bound on the optimal integer value. © 2007 South-Western College Publishing 8

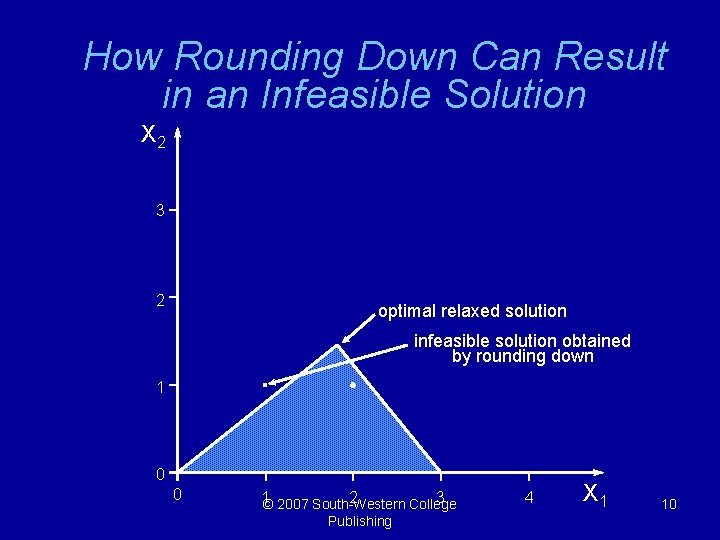
Rounding § It is tempting to simply round a fractional solution to the closest integer solution. § In general, this does not work reliably: – The rounded solution may be infeasible. – The rounded solution may be suboptimal. © 2007 South-Western College Publishing 9

How Rounding Down Can Result in an Infeasible Solution X 2 3 2 optimal relaxed solution infeasible solution obtained by rounding down 1 0 0 1© 2007 South-Western 2 3 College Publishing 4 X 1 10

Branch-and-Bound § The Branch-and-Bound (B&B) algorithm can be used to solve ILP problems. § Requires the solution of a series of LP problems termed “candidate problems”. § Theoretically, this can solve any ILP. § Practically, it often takes LOTS of computational effort (and time). © 2007 South-Western College Publishing 11

Stopping Rules § Because B&B can take so long, most ILP packages allow you to specify a suboptimality tolerance factor. § This allows you to stop once an integer solution is found that is within some % of the global optimal solution. § Bounds obtained from LP relaxations are helpful here. – Example ØLP relaxation has an optimal obj. value of $64, 306. Ø 95% of $64, 306 is $61, 090. ØThus, an integer solution with obj. value of $61, 090 or better must be within 5% of the optimal solution. © 2007 South-Western College Publishing 12

Using Solver Let’s see how to specify integrality conditions and suboptimality tolerances using Solver… See file Fig 6 -8. xls © 2007 South-Western College Publishing 13

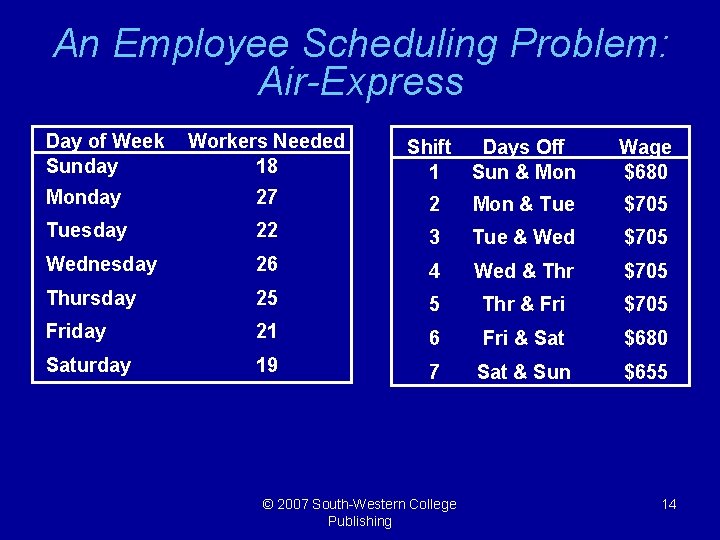
An Employee Scheduling Problem: Air-Express Day of Week Sunday Workers Needed 18 Shift Days Off 1 Sun & Mon Wage $680 Monday 27 2 Mon & Tue $705 Tuesday 22 3 Tue & Wed $705 Wednesday 26 4 Wed & Thr $705 Thursday 25 5 Thr & Fri $705 Friday 21 6 Fri & Sat $680 Saturday 19 7 Sat & Sun $655 © 2007 South-Western College Publishing 14

Defining the Decision Variables X 1 = the number of workers assigned to shift 1 X 2 = the number of workers assigned to shift 2 X 3 = the number of workers assigned to shift 3 X 4 = the number of workers assigned to shift 4 X 5 = the number of workers assigned to shift 5 X 6 = the number of workers assigned to shift 6 X 7 = the number of workers assigned to shift 7 © 2007 South-Western College Publishing 15

Defining the Objective Function Minimize the total wage expense. MIN: 680 X 1 +705 X 2 +705 X 3 +705 X 4 +705 X 5 +680 X 6 +655 X 7 © 2007 South-Western College Publishing 16

Defining the Constraints § Workers required each day 0 X 1+ 1 X 2+ 1 X 3+ 1 X 4+ 1 X 5+ 1 X 6+ 0 X 7 >= 18 } Sunday 0 X 1+ 0 X 2+ 1 X 3+ 1 X 4+ 1 X 5+ 1 X 6+ 1 X 7 >= 27 } Monday 1 X 1+ 0 X 2+ 0 X 3+ 1 X 4+ 1 X 5+ 1 X 6+ 1 X 7 >= 22 }Tuesday 1 X 1+ 1 X 2+ 0 X 3+ 0 X 4+ 1 X 5+ 1 X 6+ 1 X 7 >= 26 } Wednesday 1 X 1+ 1 X 2+ 1 X 3+ 0 X 4+ 0 X 5+ 1 X 6+ 1 X 7 >= 25 } Thursday 1 X 1+ 1 X 2+ 1 X 3+ 1 X 4+ 0 X 5+ 0 X 6+ 1 X 7 >= 21 } Friday 1 X 1+ 1 X 2+ 1 X 3+ 1 X 4+ 1 X 5+ 0 X 6+ 0 X 7 >= 19 } Saturday § Nonnegativity & integrality conditions Xi >= 0 and integer for all i © 2007 South-Western College Publishing 17

Implementing the Model See file Fig 6 -14. xls © 2007 South-Western College Publishing 18

Binary Variables § Binary variables are integer variables that can assume only two values: 0 or 1. § These variables can be useful in a number of practical modeling situations…. © 2007 South-Western College Publishing 19

A Capital Budgeting Problem: CRT Technologies Capital (in $000 s) Required in Expected NPV Project (in $000 s) Year 1 Year 2 Year 3 Year 4 Year 5 1 $141 $75 $20 $15 $10 2 $187 $90 $35 $0 $0 $30 3 $121 $60 $15 $15 4 $83 $30 $20 $10 $5 $5 5 $265 $100 $25 $20 $20 6 $127 $50 $20 $10 $30 $40 § The company has $250, 000 available to invest in new projects. It has budgeted $75, 000 for continued support for these projects in year 2 and $50, 000 per year for years 3, 4, and 5. § Unused funds in any year cannot be carried over. © 2007 South-Western College Publishing 20

Defining the Decision Variables © 2007 South-Western College Publishing 21

Defining the Objective Function Maximize the total NPV of selected projects. MAX: 141 X 1 + 187 X 2 + 121 X 3 + 83 X 4 + 265 X 5 + 127 X 6 © 2007 South-Western College Publishing 22

Defining the Constraints § Capital Constraints 75 X 1 + 90 X 2 + 60 X 3 + 30 X 4 + 100 X 5 + 50 X 6 <= 250 25 X 1 + 35 X 2 +15 X 3 + 20 X 4 + 25 X 5 + 20 X 6 <= 75 20 X 1 + 0 X 2 + 15 X 3 + 10 X 4 + 20 X 5 + 10 X 6 <= 50 15 X 1 + 0 X 2 + 15 X 3 + 5 X 4 + 20 X 5 + 30 X 6 <= 50 10 X 1 +30 X 2 +15 X 3 + 5 X 4 + 20 X 5 + 40 X 6 <= 50 } year 1 } year 2 } year 3 } year 4 } year 5 § Binary Constraints All Xi must be binary © 2007 South-Western College Publishing 23

Implementing the Model See file Fig 6 -17. xls © 2007 South-Western College Publishing 24

Binary Variables & Logical Conditions § Binary variables are also useful in modeling a number of logical conditions. – Of projects 1, 3 & 6, no more than one may be selected X 1 + X 3 + X 6 <= 1 – Of projects 1, 3 & 6, exactly one must be selected X 1 + X 3 + X 6 = 1 – Project 4 cannot be selected unless project 5 is also selected X 4 – X 5 <= 0 © 2007 South-Western College Publishing 25

The Fixed-Charge Problem § Many decisions result in a fixed or lump-sum cost being incurred: The cost to lease, rent, or purchase a piece of equipment or a vehicle that will be required if a particular action is taken. – The setup cost required to prepare a machine or to produce a different type of product. – The cost to construct a new production line that will be required if a particular decision is made. – The cost of hiring additional personnel that will be required if a particular decision is made. – © 2007 South-Western College Publishing 26

Example Fixed-Charge Problem: Remington Manufacturing Hours Required By: Operation Prod. 1 Prod. 2 Hours Available Machining 2 3 6 600 Grinding 6 3 4 300 Assembly 5 6 2 400 Unit Profit $48 $55 $50 Setup Cost $1000 $800 $900 © 2007 South-Western College Publishing Prod. 3 27

Defining the Objective Function Maximize total profit. MAX: 48 X 1 + 55 X 2 + 50 X 3 – 1000 Y 1 – 800 Y 2 – 900 Y 3 © 2007 South-Western College Publishing 28

Defining the Decision Variables Xi = the amount of product i to be produced, i = 1, 2, 3 © 2007 South-Western College Publishing 29

Defining the Constraints § Resource Constraints 2 X 1 + 3 X 2 + 6 X 3 <= 600 6 X 1 + 3 X 2 + 4 X 3 <= 300 5 X 1 + 6 X 2 + 2 X 3 <= 400 } machining } grinding } assembly § Binary Constraints All Yi must be binary § Nonnegativity conditions Xi >= 0, i = 1, 2, . . . , 6 § Is there a missing link? © 2007 South-Western College Publishing 30

Defining the Constraints (cont’d) § Linking Constraints (with “Big M”) X 1 <= M 1 Y 1 or X 1 - M 1 Y 1 <= 0 X 2 <= M 2 Y 2 or X 2 - M 2 Y 2 <= 0 X 3 <= M 3 Y 3 or X 3 - M 3 Y 3 <= 0 § If Xi > 0 these constraints force the associated Yi to equal 1. § If Xi = 0 these constraints allow Yi to equal 0 or 1, but the objective will cause Solver to choose 0. § Note that Mi imposes an upper bounds on Xi. § It helps to find reasonable values for the Mi. © 2007 South-Western College Publishing 31

Finding Reasonable Values for M 1 § Consider the resource constraints 2 X 1 + 3 X 2 + 6 X 3 <= 600 6 X 1 + 3 X 2 + 4 X 3 <= 300 5 X 1 + 6 X 2 + 2 X 3 <= 400 } machining } grinding } assembly § What is the maximum value X 1 can assume? Let X 2 = X 3 = 0 X 1 = MIN(600/2, 300/6, 400/5) = MIN(300, 50, 80) = 50 § Maximum values for X 2 & X 3 can be found similarly. © 2007 South-Western College Publishing 32

Summary of the Model MAX: 48 X 1 + 55 X 2 + 50 X 3 - 1000 Y 1 - 800 Y 2 - 900 Y 3 S. T. : 2 X 1 + 3 X 2 + 6 X 3 <= 600 } machining 6 X 1 + 3 X 2 + 4 X 3 <= 300 } grinding 5 X 1 + 6 X 2 + 2 X 3 <= 400 } assembly X 1 - 50 Y 1 <= 0 X 2 - 67 Y 2 <= 0 linking constraints X 3 - 75 Y 3 <= 0 All Yi must be binary Xi >= 0, i = 1, 2, 3 © 2007 South-Western College Publishing 33

Potential Pitfall § Do not use IF( ) functions to model the relationship between the Xi and Yi. – Suppose cell A 5 represents X 1 – Suppose cell A 6 represents Y 1 – You’ll want to let A 6 = IF(A 5>0, 1, 0) – This will not work with Solver! § Treat the Yi just like any other variable. – Make them changing cells. – Use the linking constraints to enforce the proper relationship between the Xi and Yi. © 2007 South-Western College Publishing 34

Implementing the Model See file Fig 6 -21. xls © 2007 South-Western College Publishing 35

Minimum Order Size Restrictions Suppose Remington doesn’t want to manufacture any units of product 3 unless it produces at least 40 units. . . Consider, X 3 <= M 3 Y 3 X 3 >= 40 Y 3 © 2007 South-Western College Publishing 36

Quantity Discounts § Assume… – If Blue Ridge Hot Tubs produces more than 75 Aqua-Spas, it obtains discounts that increase the unit profit to $375. – If it produces more than 50 Hydro. Luxes, the profit increases to $325. © 2007 South-Western College Publishing 37

Quantity Discount Model MAX: 350 X 11 + 375 X 12 + 300 X 21 + 325 X 22 S. T. : 1 X 11 + 1 X 12 + 1 X 21 + 1 X 22 <= 200 } pumps 9 X 11 + 9 X 12 + 6 X 21 + 6 X 22 <= 1566 } labor 12 X 11+ 12 X 12+ 16 X 21+16 X 22 <= 2880 } tubing X 12<=M 12 Y 1 X 11>=75 Y 1 X 22<=M 22 Y 2 X 21>=50 Y 2 Xij >= 0 Xij must be integers, Yi must be binary © 2007 South-Western College Publishing 38

A Contract Award Problem § B&G Construction has 4 building projects and can purchase cement from 3 companies for the following costs: Co. 1 Co. 2 Co. 3 Needs (tons) Cost per Delivered Ton of Cement Max. Project 1 Project 2 Project 3 Project 4 Supply $120 $115 $130 $125 525 $100 $150 $110 $105 450 $140 $95 $145 $165 550 450 275 300 350 © 2007 South-Western College Publishing 39

A Contract Award Problem § Side constraints: – Co. 1 will not supply orders of less than 150 tons for any project – Co. 2 can supply more than 200 tons to no more than one of the projects – Co. 3 will accept only orders that total 200, 400, or 550 tons © 2007 South-Western College Publishing 40

Defining the Decision Variables Xij = tons of cement purchased from company i for project j © 2007 South-Western College Publishing 41

Defining the Objective Function Minimize total cost MIN: 120 X 11 + 115 X 12 + 130 X 13 + 125 X 14 + 100 X 21 + 150 X 22 + 110 X 23 + 105 X 24 + 140 X 31 + 95 X 32 + 145 X 33 + 165 X 34 © 2007 South-Western College Publishing 42

Defining the Constraints § Supply Constraints X 11 + X 12 + X 13 + X 14 <= 525 } company 1 X 21 + X 22 + X 23 + X 24 <= 450 } company 2 X 31 + X 32 + X 33 + X 34 <= 550 } company 3 § Demand Constraints X 11 + X 21 + X 31 = 450 X 12 + X 22 + X 32 = 275 X 13 + X 23 + X 33 = 300 X 14 + X 24 + X 34 = 350 } project 1 } project 2 } project 3 } project 4 © 2007 South-Western College Publishing 43

Implementing the Transportation Constraints See file Fig 6 -25. xls © 2007 South-Western College Publishing 44

Defining the Constraints-I § Company 1 Side Constraints X 11<=525 Y 11 X 12<=525 Y 12 X 13<=525 Y 13 X 14<=525 Y 14 X 11>=150 Y 11 X 12>=150 Y 12 X 13>=150 Y 13 X 14>=150 Y 14 Yij binary© 2007 South-Western College Publishing 45

Defining the Constraints-II § Company 2 Side Constraints X 21<=200+250 Y 21 X 22<=200+250 Y 22 X 23<=200+250 Y 23 X 24<=200+250 Y 24 Y 21 + Y 22 + Y 23 + Y 24 <= 1 Yij binary © 2007 South-Western College Publishing 46

Defining the Constraints-III § Company 3 Side Constraints X 31 + X 32 + X 33 + X 34 = 200 Y 31 + 400 Y 32 + 550 Y 33 Y 31 + Y 32 + Y 33 <= 1 © 2007 South-Western College Publishing 47

Implementing the Side Constraints See file Fig 6 -25. xls © 2007 South-Western College Publishing 48

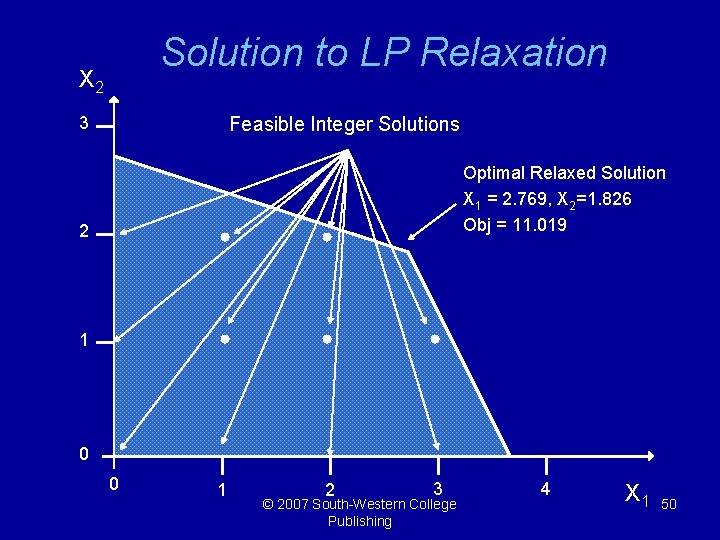
The Branch-And-Bound Algorithm MAX: 2 X 1 + 3 X 2 S. T. X 1 + 3 X 2 <= 8. 25 2. 5 X 1 + X 2 <= 8. 75 X 1, X 2 >= 0 and integer © 2007 South-Western College Publishing 49

Solution to LP Relaxation X 2 3 Feasible Integer Solutions Optimal Relaxed Solution X 1 = 2. 769, X 2=1. 826 Obj = 11. 019 2 1 0 0 1 2 3 © 2007 South-Western College Publishing 4 X 1 50

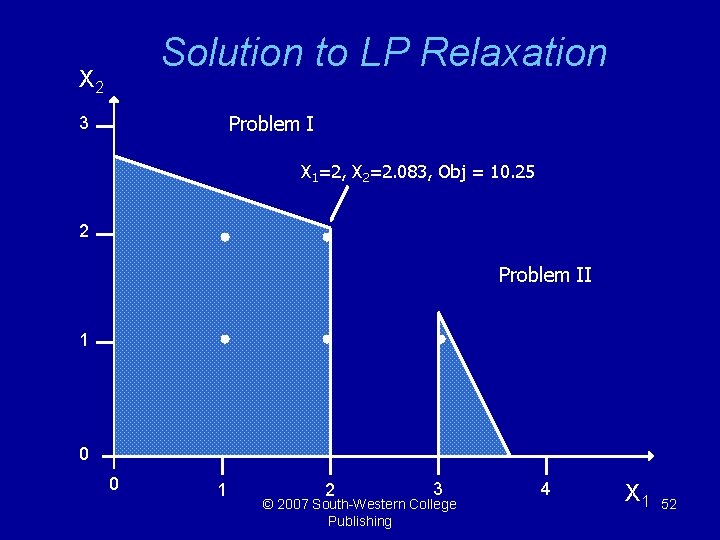
The Branch-And-Bound Algorithm Problem I MAX: 2 X 1 + 3 X 2 S. T. X 1 + 3 X 2 <= 8. 25 2. 5 X 1 + X 2 <= 8. 75 X 1 <= 2 X 1, X 2 >= 0 and integer Problem II MAX: 2 X 1 + 3 X 2 S. T. X 1 + 3 X 2 <= 8. 25 2. 5 X 1 + X 2 <= 8. 75 X 1 >= 3 X 1, X 2 >= 0 and integer © 2007 South-Western College Publishing 51

Solution to LP Relaxation X 2 Problem I 3 X 1=2, X 2=2. 083, Obj = 10. 25 2 Problem II 1 0 0 1 2 3 © 2007 South-Western College Publishing 4 X 1 52

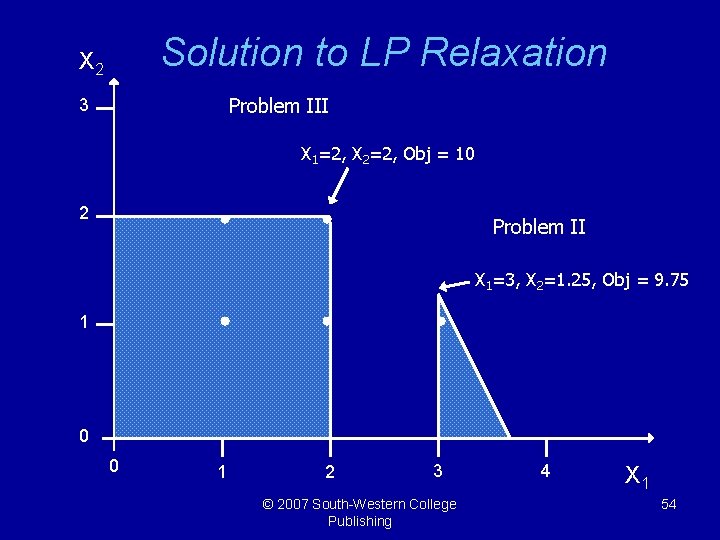
The Branch-And-Bound Algorithm Problem III MAX: S. T. 2 X 1 + 3 X 2 <= 8. 25 2. 5 X 1 + X 2 <= 8. 75 X 1 <= 2 X 2 <= 2 X 1, X 2 >= 0 and integer Problem IV MAX: 2 X 1 + 3 X 2 S. T. X 1 + 3 X 2 <= 8. 25 2. 5 X 1 + X 2 <= 8. 75 X 1 <= 2 X 2 >= 3 X 1, X 2 College >= 0 © 2007 South-Western Publishing and integer 53

Solution to LP Relaxation X 2 Problem III 3 X 1=2, X 2=2, Obj = 10 2 Problem II X 1=3, X 2=1. 25, Obj = 9. 75 1 0 0 1 2 3 © 2007 South-Western College Publishing 4 X 1 54

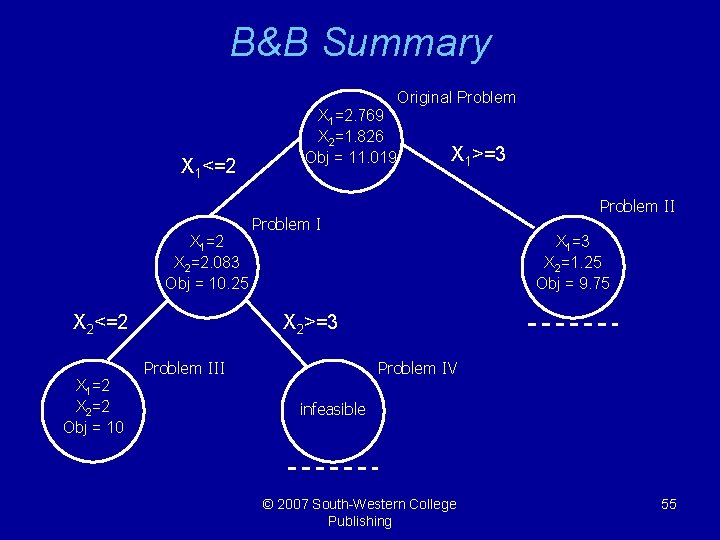
B&B Summary X 1<=2 X 1=2 X 2=2. 083 Obj = 10. 25 X 2<=2 X 1=2 X 2=2 Obj = 10 X 1=2. 769 X 2=1. 826 Obj = 11. 019 Original Problem X 1>=3 Problem II Problem I X 1=3 X 2=1. 25 Obj = 9. 75 X 2>=3 Problem III Problem IV infeasible © 2007 South-Western College Publishing 55

End of Chapter 6 © 2007 South-Western College Publishing 56