Sponsored by Navigation in Urban Areas 98 th

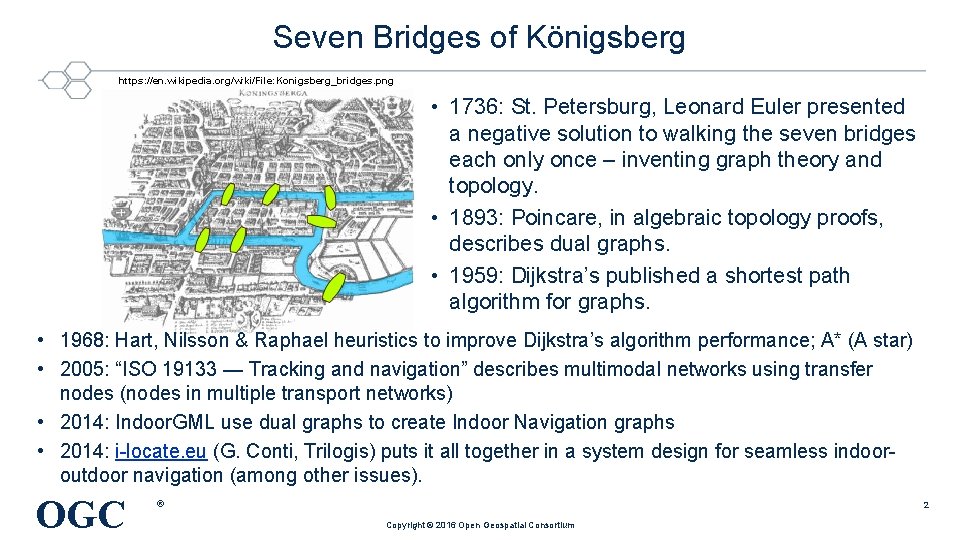
Seven Bridges of Königsberg https: //en. wikipedia. org/wiki/File: Konigsberg_bridges. png • 1736: St. Petersburg, Leonard Euler presented a negative solution to walking the seven bridges each only once – inventing graph theory and topology. • 1893: Poincare, in algebraic topology proofs, describes dual graphs. • 1959: Dijkstra’s published a shortest path algorithm for graphs. • 1968: Hart, Nilsson & Raphael heuristics to improve Dijkstra’s algorithm performance; A* (A star) • 2005: “ISO 19133 — Tracking and navigation” describes multimodal networks using transfer nodes (nodes in multiple transport networks) • 2014: Indoor. GML use dual graphs to create Indoor Navigation graphs • 2014: i-locate. eu (G. Conti, Trilogis) puts it all together in a system design for seamless indooroutdoor navigation (among other issues). OGC ® 2 Copyright © 2016 Open Geospatial Consortium

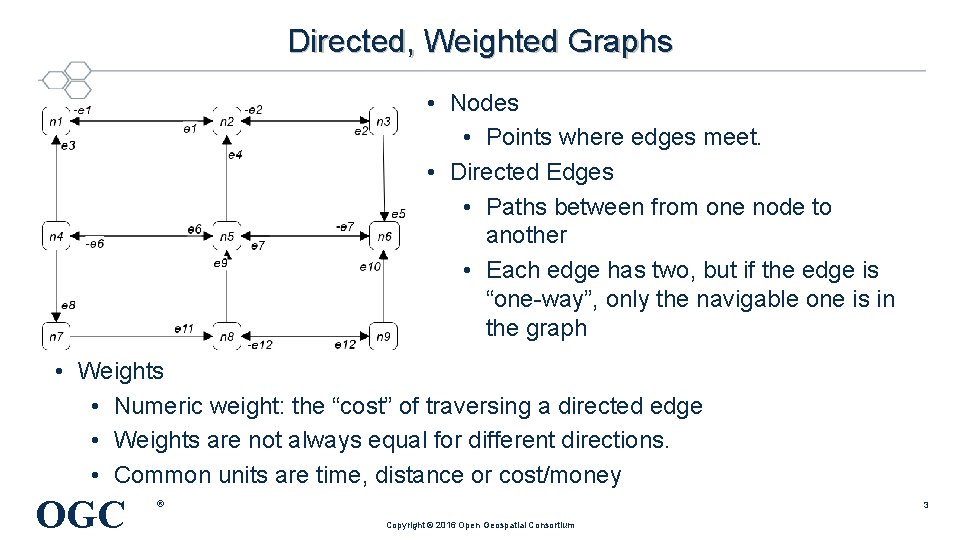
Directed, Weighted Graphs • Nodes • Points where edges meet. • Directed Edges • Paths between from one node to another • Each edge has two, but if the edge is “one-way”, only the navigable one is in the graph • Weights • Numeric weight: the “cost” of traversing a directed edge • Weights are not always equal for different directions. • Common units are time, distance or cost/money OGC ® 3 Copyright © 2016 Open Geospatial Consortium

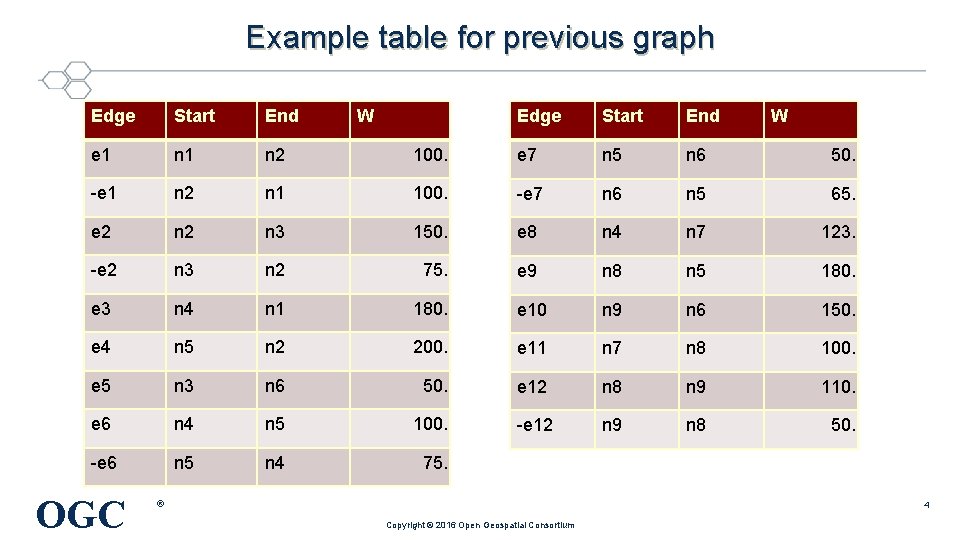
Example table for previous graph Edge Start End 100. e 7 n 5 n 6 50. n 1 100. -e 7 n 6 n 5 65. n 2 n 3 150. e 8 n 4 n 7 123. -e 2 n 3 n 2 75. e 9 n 8 n 5 180. e 3 n 4 n 1 180. e 10 n 9 n 6 150. e 4 n 5 n 2 200. e 11 n 7 n 8 100. e 5 n 3 n 6 50. e 12 n 8 n 9 110. e 6 n 4 n 5 100. -e 12 n 9 n 8 50. -e 6 n 5 n 4 75. Edge Start End e 1 n 2 -e 1 n 2 e 2 OGC W ® W 4 Copyright © 2016 Open Geospatial Consortium

Dijkstra's algorithm • Finds shortest paths (weights) from one node to another. – The base algorithm is exhaustive. • “A*” variant uses a lower bound distance function between nodes such that d(n 1, n 2) ≤ path-length(n 1, n 2). – Most distancenavigation algorithm use A* with “d” geodesic distance • Dijkstra's algorithm is well and often documented – Wikipedia article on it is accurate. • The best-practice navigation optimization is the use of Dijkstra or A* with variations on “distance”, “time” or “cost”. – e. g. Google Maps on transit routes takes “transfer time” into account for metro routes (as least suggested by “backward engineering”) OGC ® 5 Copyright © 2016 Open Geospatial Consortium

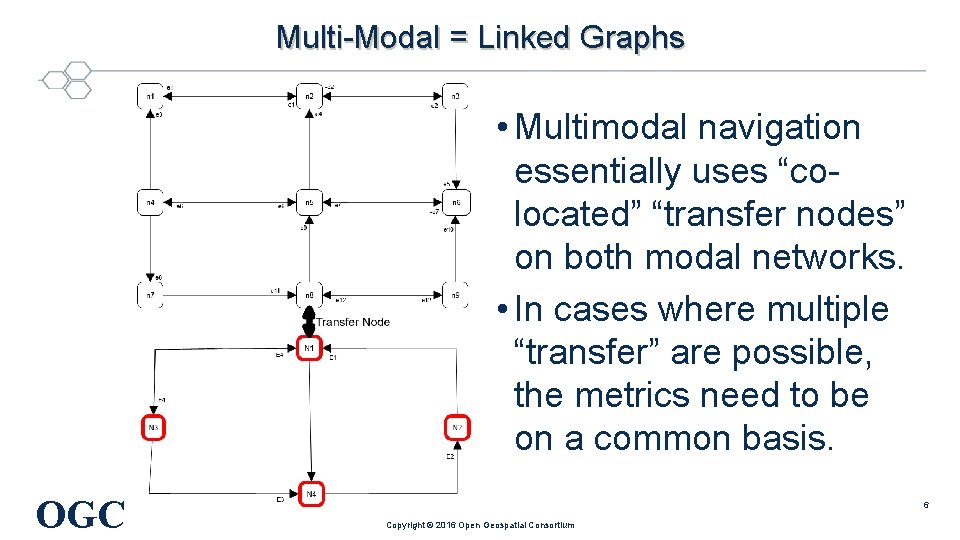
Multi-Modal = Linked Graphs • Multimodal navigation essentially uses “colocated” “transfer nodes” on both modal networks. • In cases where multiple “transfer” are possible, the metrics need to be on a common basis. OGC ® 6 Copyright © 2016 Open Geospatial Consortium

Poincaré duality (1893) dual graphs • The Poincaré dual of a “face-edge-node” graph – face to node – node to face, – boundary edges to adjacency linkages OGC • Area-boundary-area navigation becomes node-edge-node navigation • Adjacency graph becomes connectivity graph by keeping only “accessible” link (with doors) • Thiessen polygons ↔ TIN ® 7 Copyright © 2016 Open Geospatial Consortium

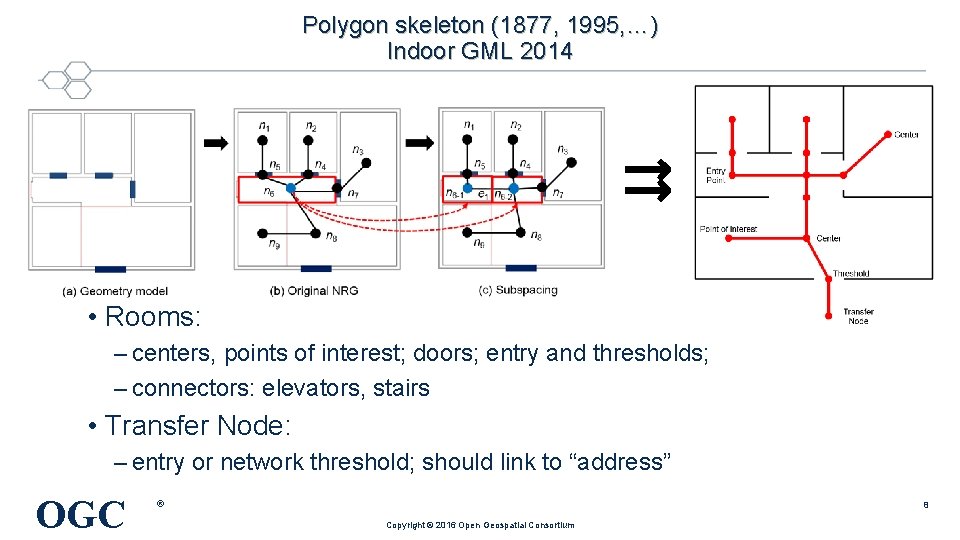
Polygon skeleton (1877, 1995, …) Indoor GML 2014 ⇉ • Rooms: – centers, points of interest; doors; entry and thresholds; – connectors: elevators, stairs • Transfer Node: – entry or network threshold; should link to “address” OGC ® 8 Copyright © 2016 Open Geospatial Consortium

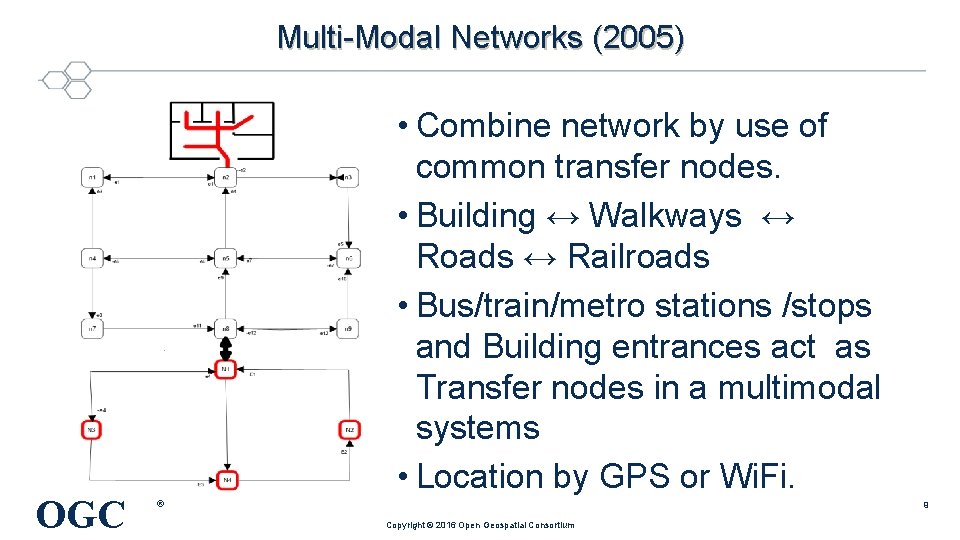
Multi-Modal Networks (2005) OGC • Combine network by use of common transfer nodes. • Building ↔ Walkways ↔ Roads ↔ Railroads • Bus/train/metro stations /stops and Building entrances act as Transfer nodes in a multimodal systems • Location by GPS or Wi. Fi. ® 9 Copyright © 2016 Open Geospatial Consortium

Proof of concepts & System Design: • Indoor/outdoor location and asset management through open geodata; (2014 -present) – i-locate: http: //www. i-locate. eu/ – Designs, Open source implementations, Pilots – Blog from OGC: http: //www. opengeospatial. org/blog/2263 • OGC members involved: – Giuseppe Conti, Trilogis (Project Coordinator) – Prof. Ki-Joune Li, Pusan National University (Indoor. GML) OGC ® 10 Copyright © 2016 Open Geospatial Consortium