SPM short course Mai 2008 Linear Models and

SPM short course – Mai 2008 Linear Models and Contrasts Jean-Baptiste Poline Neurospin, I 2 BM, CEA Saclay, France

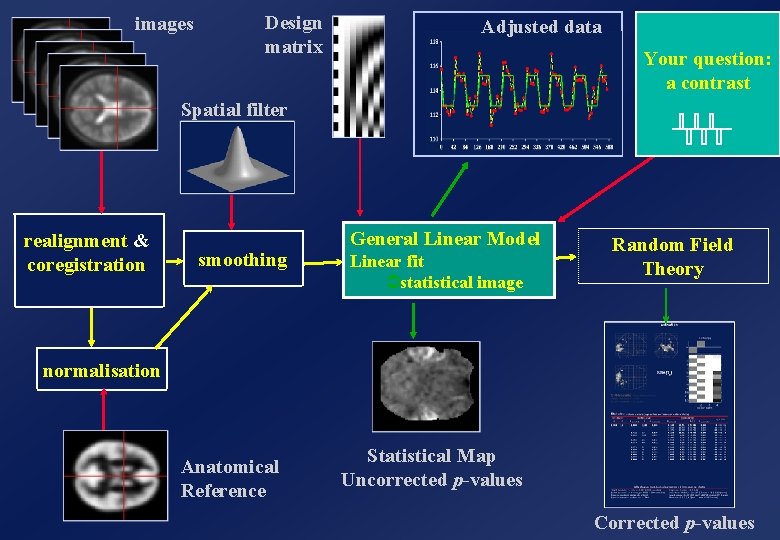
images Design matrix Adjusted data Your question: a contrast Spatial filter realignment & coregistration smoothing General Linear Model Linear fit Ü statistical image Random Field Theory normalisation Anatomical Reference Statistical Map Uncorrected p-values Corrected p-values

Plan w REPEAT: model and fitting the data with a Linear Model w Make sure we understand the testing procedures : t- and F-tests w But what do we test exactly ? w Examples – almost real

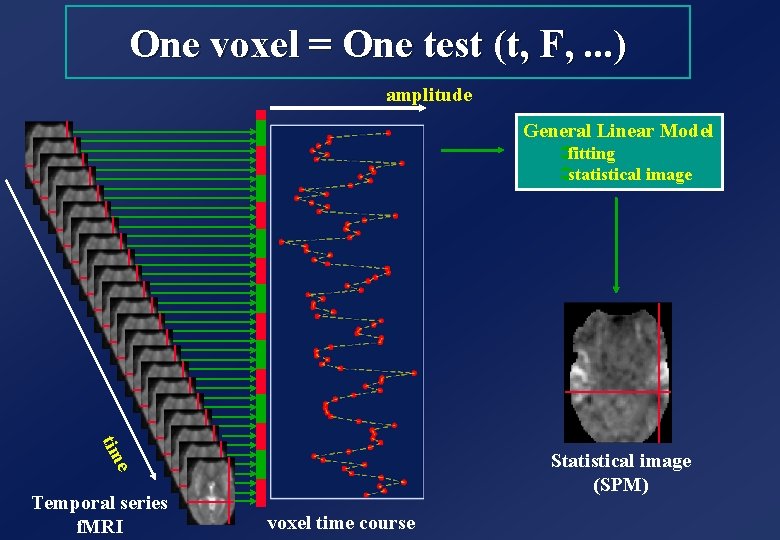
One voxel = One test (t, F, . . . ) amplitude General Linear Model Üfitting Üstatistical image tim e Statistical image (SPM) Temporal series f. MRI voxel time course

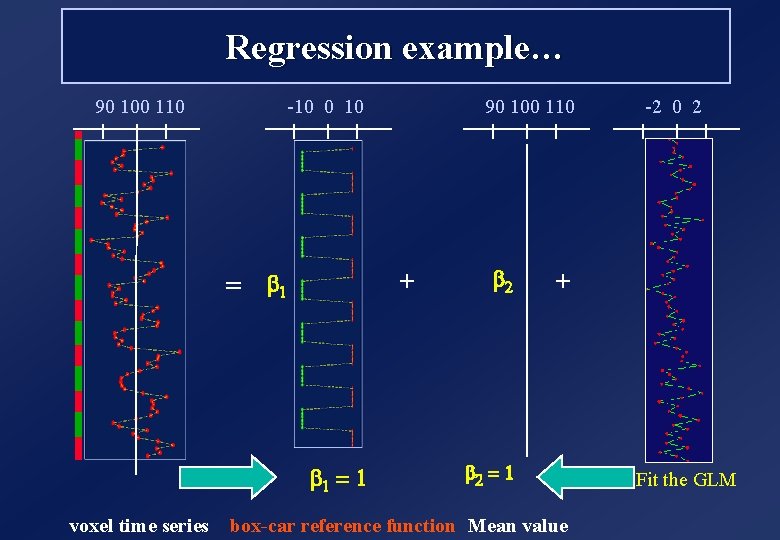
Regression example… 90 100 110 -10 0 10 + = b 1 = 1 voxel time series 90 100 110 b 2 -2 0 2 + b 2 = 1 box-car reference function Mean value Fit the GLM

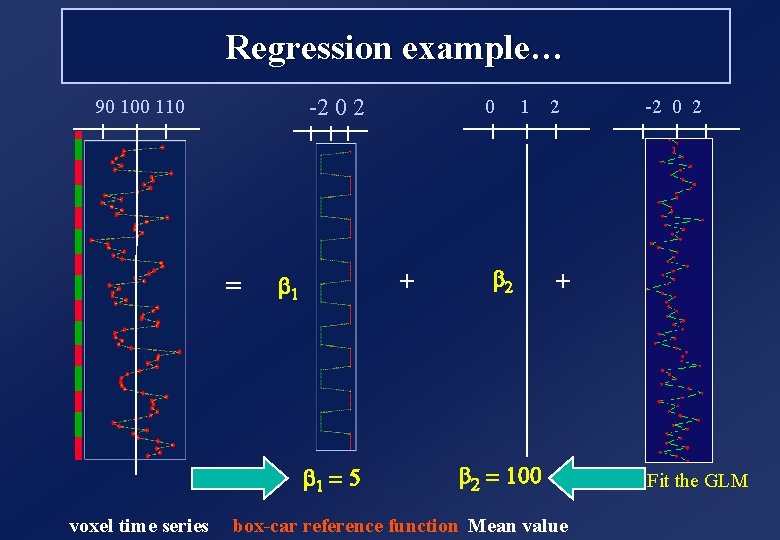
Regression example… -2 0 2 90 100 110 = + b 1 = 5 voxel time series 0 1 b 2 2 -2 0 2 + b 2 = 100 box-car reference function Mean value Fit the GLM

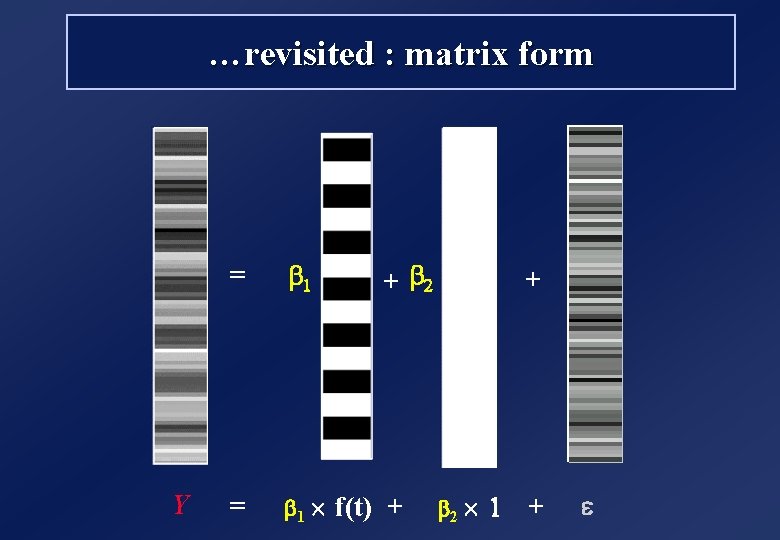
…revisited : matrix form Y + b 2 = b 1 ´ f(t) + + b 2 ´ 1 + e

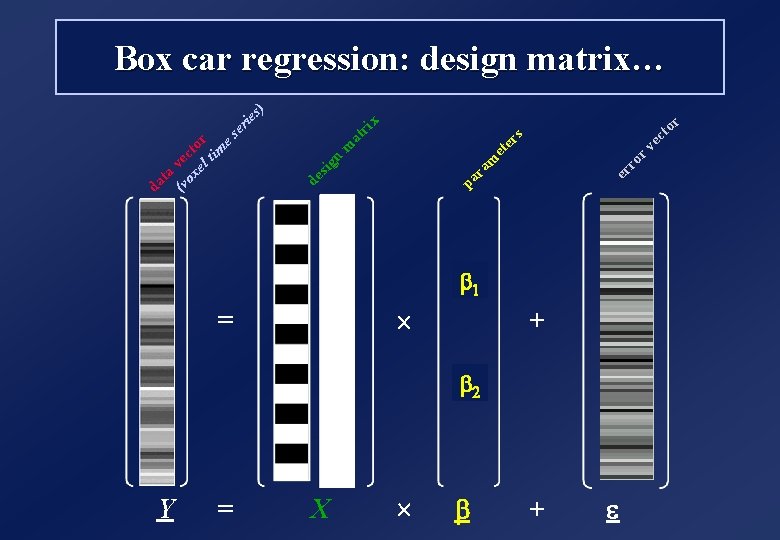
Y = = X ´ ´ b r to ec r v ro er s x er ie ri at er et m ra pa m n de sig (v vec ox to el r tim es ta da s) Box car regression: design matrix… ab 1 + m 2 b + e

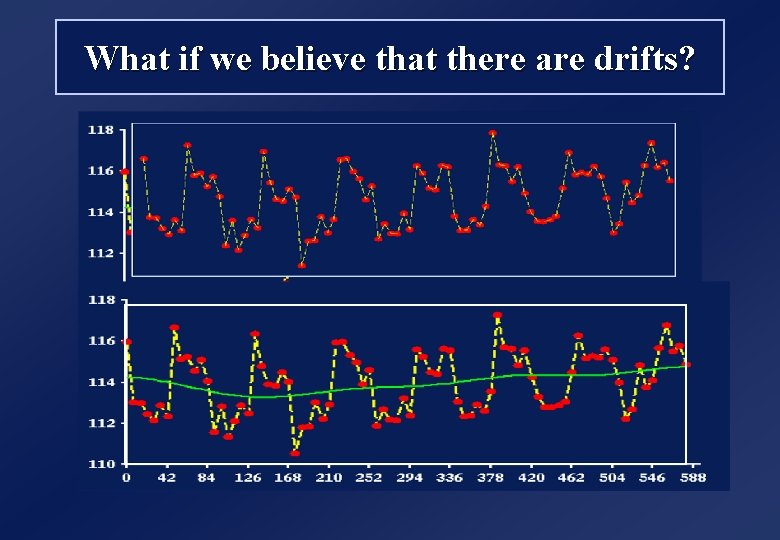
What if we believe that there are drifts?

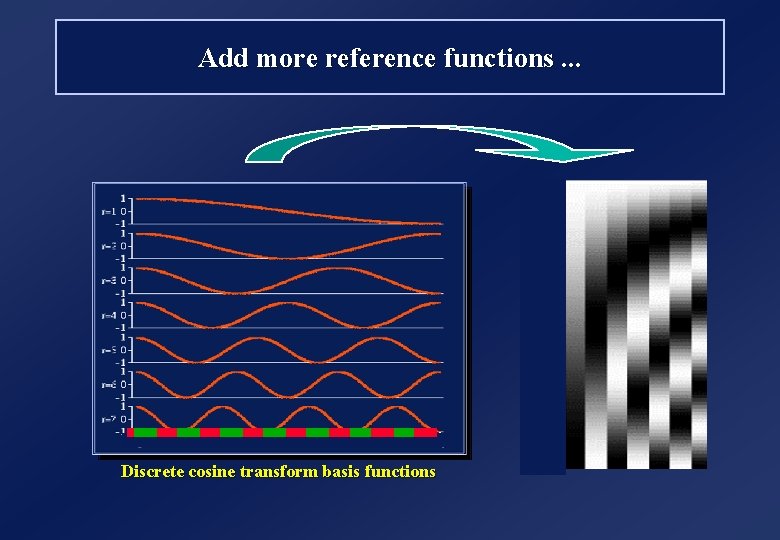
Add more reference functions. . . Discrete cosine transform basis functions

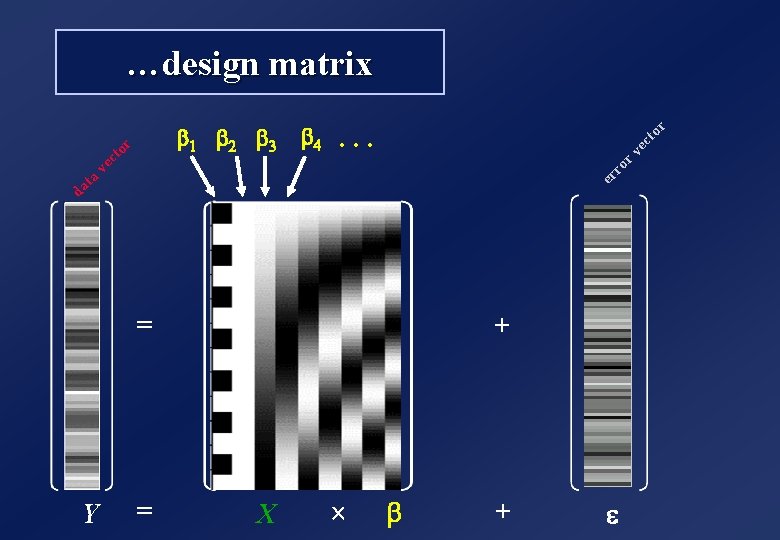
…design matrix ec to r … r v b 4 da ta er v ro ec to r b 1 b 2 b 3 + = Y = X ´ b + e

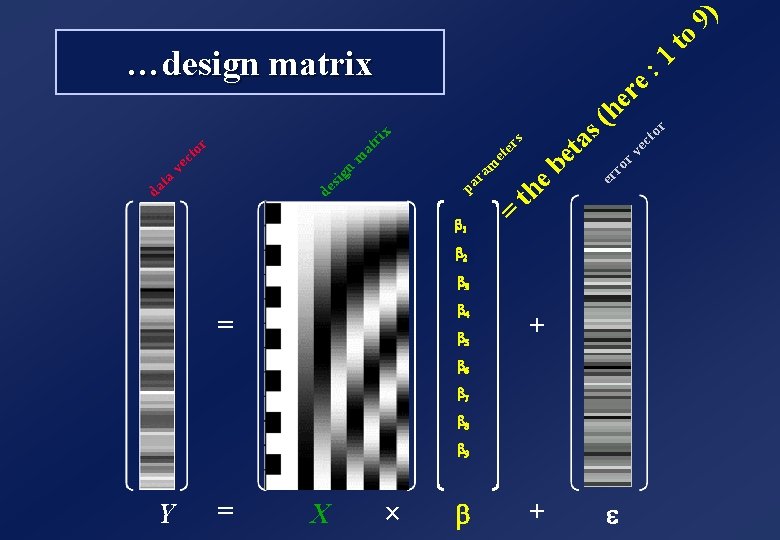
Y = X ba 1 = b 4 b 5 ´ b s er et ri x + 1 he r v re ec : to r ro er s ( e b et a th = m ra pa at n m de sig r to ec v ta da ) to 9 …design matrix bm 2 b 3 + b 6 b 7 b 8 b 9 e

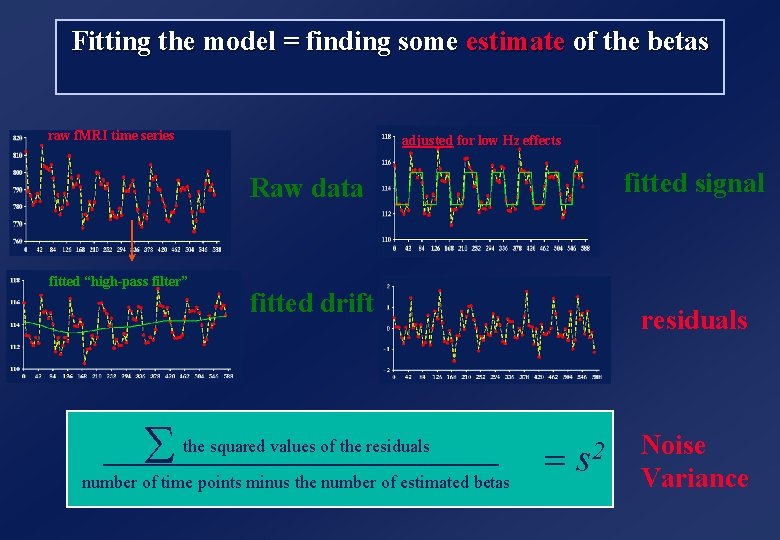
Fitting the model = finding some estimate of the betas raw f. MRI time series adjusted for low Hz effects fitted signal Raw data fitted “high-pass filter” S fitted drift the squared values of the residuals number of time points minus the number of estimated betas residuals = s 2 Noise Variance

Fitting the model = finding some estimate of the betas b 1 = b 2 b 5 b 6 + Y = X b + e b 7. . . finding the betas = minimising the sum of square of the residuals 2 ∥Y−X � ∥ 2 = Σi [ yi−� X �� ] i when b are estimated: let’s call them b when e is estimated : let’s call it e estimated SD of e : let’s call it s

Take home. . . w We put in our model regressors (or covariates) that represent how we think the signal is varying (of interest and of no interest alike) BUT WHICH ONE TO INCLUDE ? w Coefficients (= parameters) are estimated by minimizing the fluctuations, - variability – variance – of the noise – the residuals. w Because the parameters depend on the scaling of the regressors included in the model, one should be careful in comparing manually entered regressors

Plan w Make sure we all know about the estimation (fitting) part. . w Make sure we understand t and F tests w But what do we test exactly ? w An example – almost real

T test - one dimensional contrasts - SPM{t} A contrast = a weighted sum of parameters: c´ ´ b c’ = 1 0 0 0 0 b 1 > 0 ? Compute 1 xb 1 + 0 xb 2 + 0 xb 3 + 0 xb 4 + 0 xb 5 +. . . b 1 b 2 b 3 b 4 b 5. . divide by estimated standard deviation of b 1 T = contrast of estimated parameters variance estimate c’b T = s 2 c’(X’X)-c SPM{t}

How is this computed ? (t-test) Estimation [Y, X] [b, s] Y=Xb+e e ~ s 2 N(0, I) b = (X’X)+ X’Y (b: estimate of b) -> beta? ? ? images e = Y - Xb (e: estimate of e) s 2 = (e’e/(n - p)) (s: estimate of s, n: time points, p: parameters) -> 1 image Res. MS (Y : at one position) Test [b, s 2, c] [c’b, t] Var(c’b) = s 2 c’(X’X)+c t = c’b / sqrt(s 2 c’(X’X)+c) s (compute for each contrast c, proportional to 2) c’b -> images spm_con? ? ? compute the t images -> images spm_t? ? ? under the null hypothesis H 0 : t ~ Student-t( df ) df = n-p

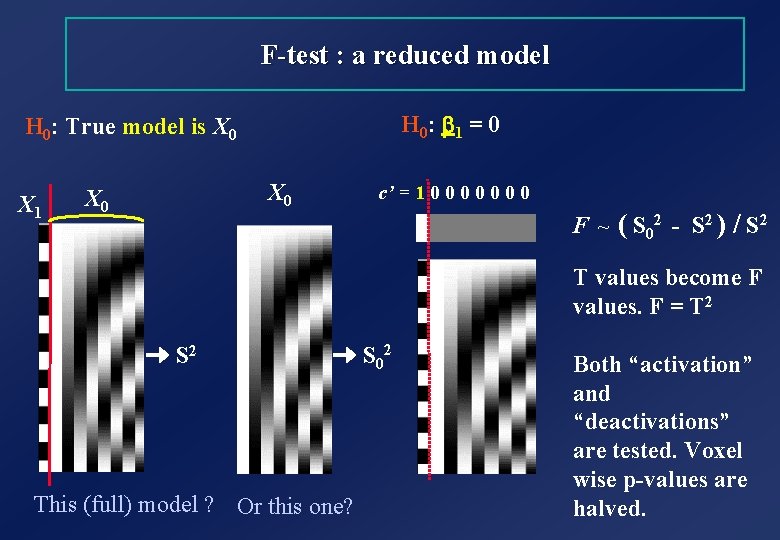
F-test : a reduced model H 0: b 1 = 0 H 0: True model is X 0 X 1 X 0 c’ = 1 0 0 0 0 F ~ ( S 02 - S 2 ) / S 2 T values become F values. F = T 2 S 2 This (full) model ? Or this one? S 02 Both “activation” and “deactivations” are tested. Voxel wise p-values are halved.

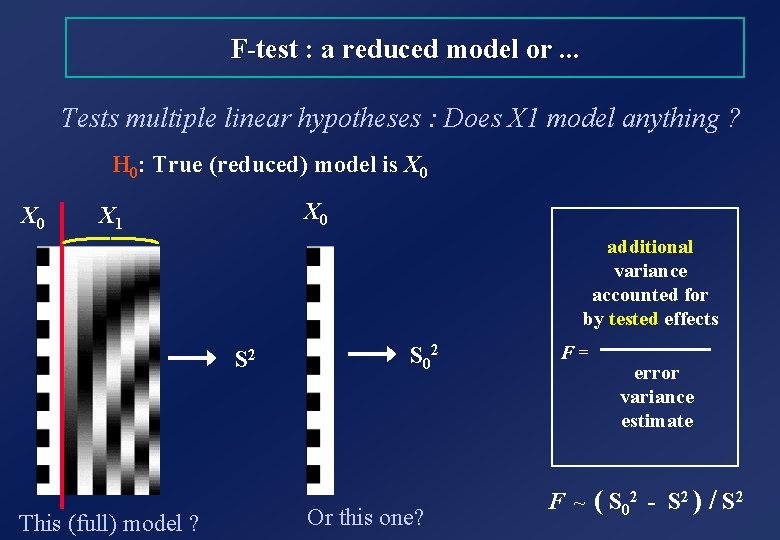
F-test : a reduced model or. . . Tests multiple linear hypotheses : Does X 1 model anything ? H 0: True (reduced) model is X 0 X 0 X 1 additional variance accounted for by tested effects S 2 This (full) model ? S 02 Or this one? F = error variance estimate F ~ ( S 02 - S 2 ) / S 2

F-test : a reduced model or. . . multi-dimensional contrasts ? tests multiple linear hypotheses. Ex : does drift functions model anything? H 0: True model is X 0 X 1 X 0 This (full) model ? Or this one? H 0: b 3 -9 = (0 0 0 0. . . ) 0 0 1 0 0 c’ = 0 0 0 0 1 0 0 0 0 1

How is this computed ? (F-test) additional variance accounted for by tested effects Error variance estimate Estimation [Y, X] [b, s] Y=Xb+e Y = X 0 b 0 + e 0 e ~ N(0, s 2 I) e 0 ~ N(0, s 02 I) X 0 : X Reduced Test [b, s, c] [ess, F] F ~ (s 0 - s) / s 2 -> image spm_ess? ? ? -> image of F : spm_F? ? ? under the null hypothesis : F ~ F(p - p 0, n-p)

T and F test: take home. . . w T tests are simple combinations of the betas; they are either positive or negative (b 1 – b 2 is different from b 2 – b 1) w F tests can be viewed as testing for the additional variance explained by a larger model wrt a simpler model, or w F tests the sum of the squares of one or several combinations of the betas w in testing “single contrast” with an F test, for ex. b 1 – b 2, the result will be the same as testing b 2 – b 1. It will be exactly the square of the t-test, testing for both positive and negative effects.

Plan w Make sure we all know about the estimation (fitting) part. . w Make sure we understand t and F tests w But what do we test exactly ? Correlation between regressors w An example – almost real

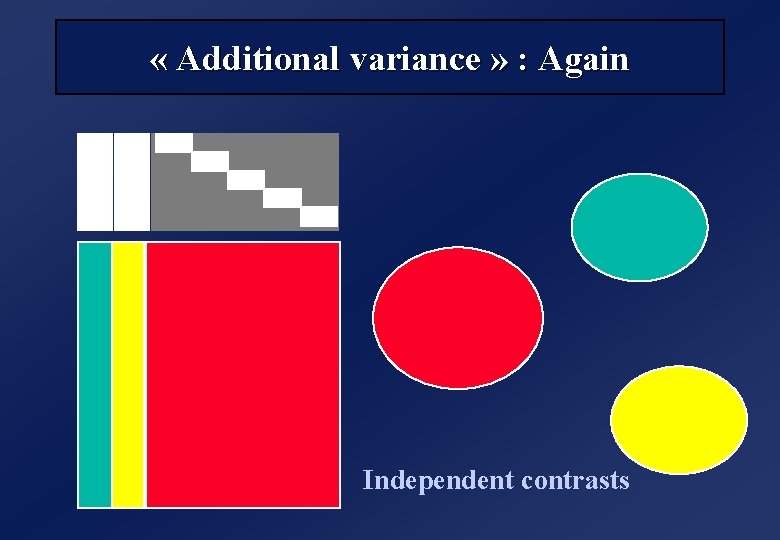
« Additional variance » : Again Independent contrasts

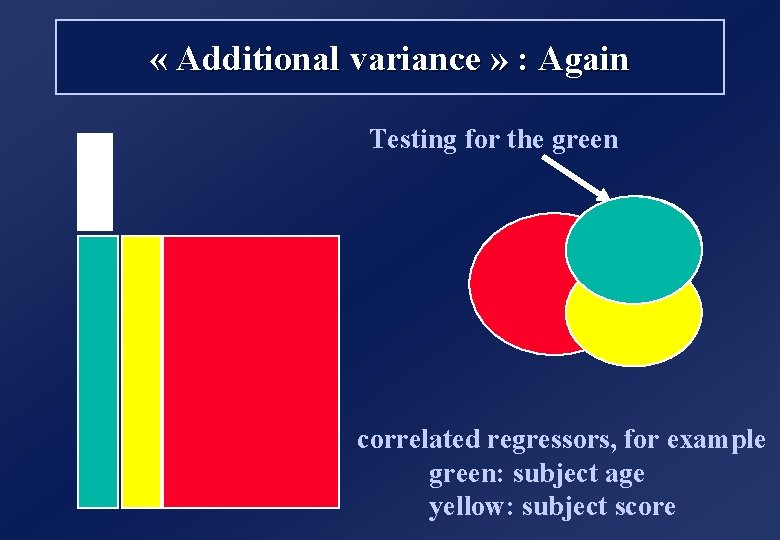
« Additional variance » : Again Testing for the green correlated regressors, for example green: subject age yellow: subject score

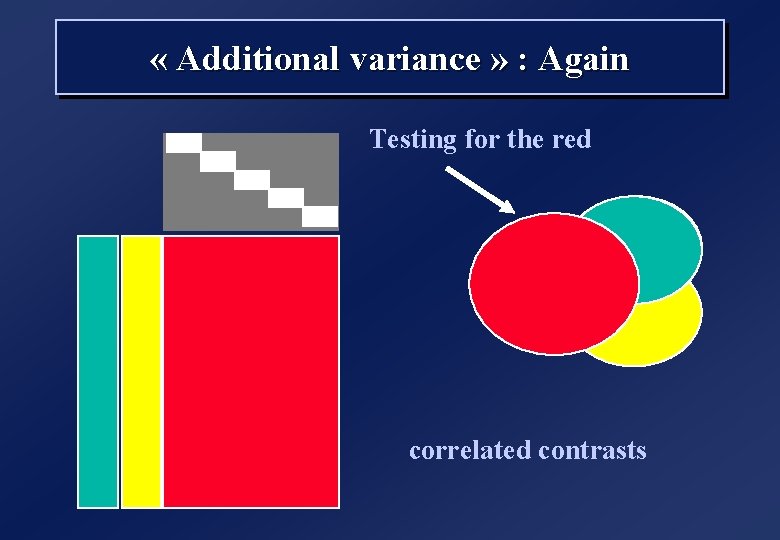
« Additional variance » : Again Testing for the red correlated contrasts

« Additional variance » : Again Testing for the green Entirely correlated contrasts ? Non estimable !

« Additional variance » : Again Testing for the green and yellow If significant ? Could be G or Y ! Entirely correlated contrasts ? Non estimable !

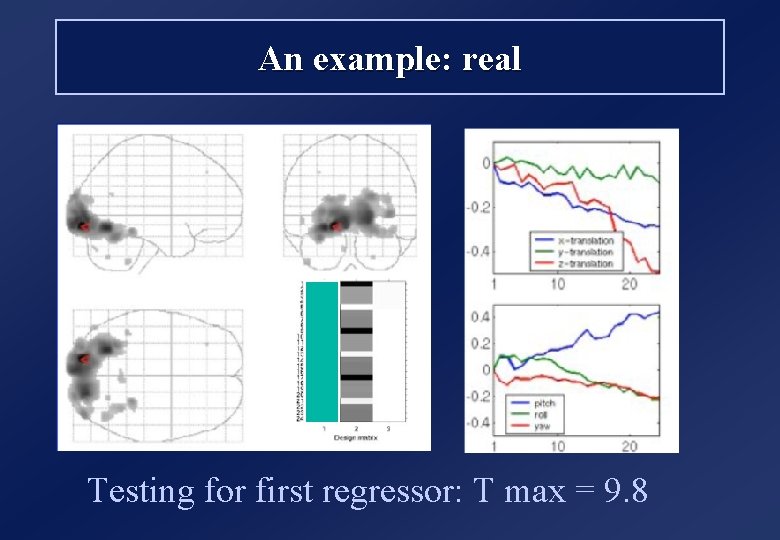
An example: real Testing for first regressor: T max = 9. 8

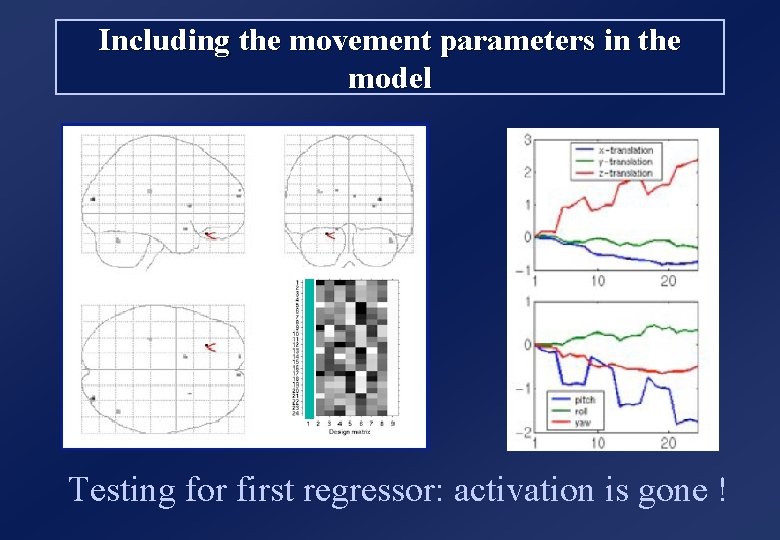
Including the movement parameters in the model Testing for first regressor: activation is gone !

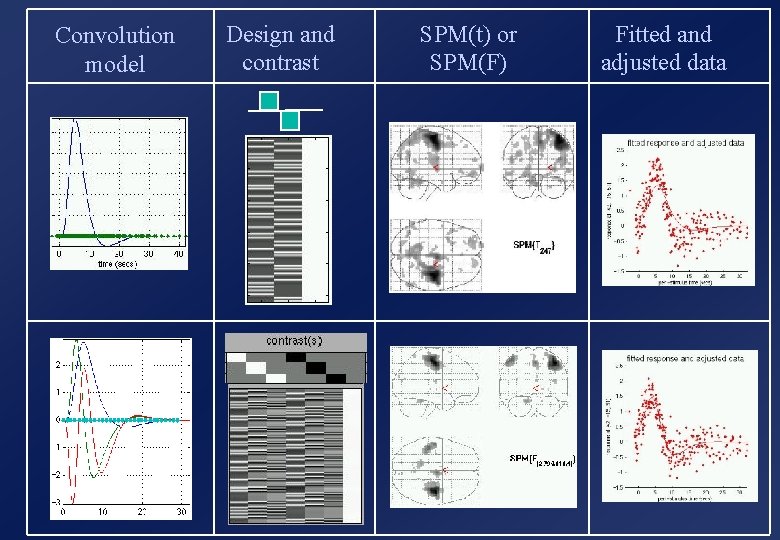
Convolution model Design and contrast SPM(t) or SPM(F) Fitted and adjusted data

Plan w Make sure we all know about the estimation (fitting) part. . w Make sure we understand t and F tests w But what do we test exactly ? Correlation between regressors w An example – almost real

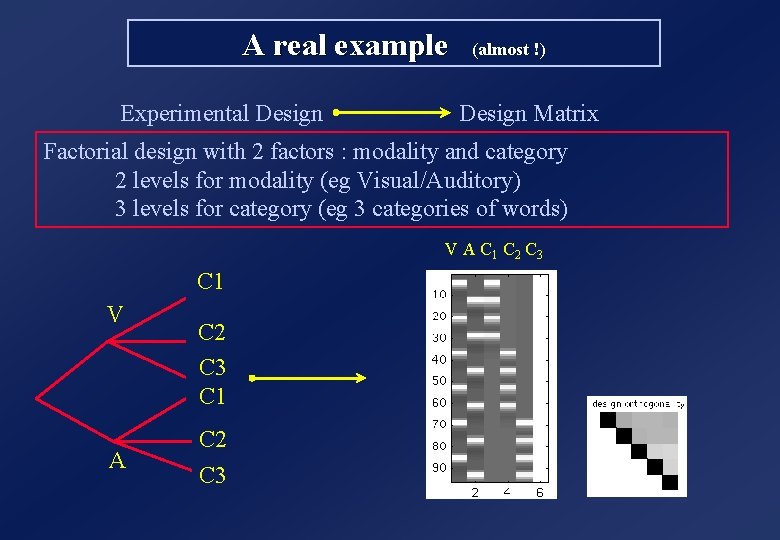
A real example (almost !) Experimental Design Matrix Factorial design with 2 factors : modality and category 2 levels for modality (eg Visual/Auditory) 3 levels for category (eg 3 categories of words) V A C 1 C 2 C 3 C 1 V A C 2 C 3 C 1 C 2 C 3

Asking ourselves some questions. . . V A C 1 C 2 C 3 Test C 1 > C 2 Test V > A Test C 1, C 2, C 3 ? (F) : c = [ 0 0 1 -1 0 0 ] : c = [ 1 -1 0 0 ] [001000] c= [000100] [000010] Test the interaction Mx. C ? • Design Matrix not orthogonal • Many contrasts are non estimable • Interactions Mx. C are not modelled

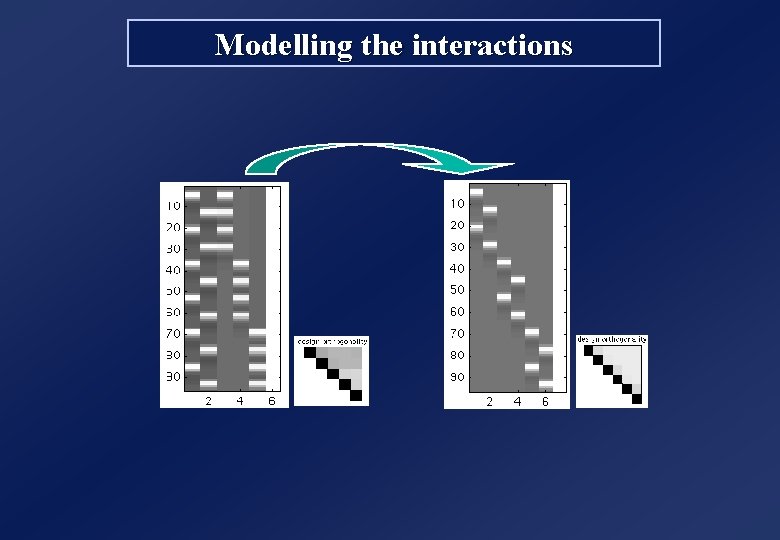
Modelling the interactions

Asking ourselves some questions. . . C 1 C 2 C 3 VAVAVA Test C 1 > C 2 : c = [ 1 1 -1 -1 0 0 0] Test V > A : c = [ 1 -1 0] Test the category effect : c= [ 1 1 -1 -1 0 0 0] [ 0 0 1 1 -1 -1 0] [ 1 1 0 0 -1 -1 0] c= [ 1 -1 -1 1 0 0 0] [ 0 0 1 -1 -1 1 0] [ 1 -1 0 0 -1 1 0] Test the interaction Mx. C : • Design Matrix orthogonal • All contrasts are estimable • Interactions Mx. C modelled • If no interaction. . . ? Model is too “big” !

Asking ourselves some questions. . . With a more flexible model C 1 C 2 C 3 VAVAVA Test C 1 > C 2 ? Test C 1 different from C 2 ? from c = [ 1 1 -1 -1 0 0 0] to c = [ 1 0 -1 0 0 0 0] [ 0 1 0 -1 0 0 0] becomes an F test! Test V > A ? c = [ 1 0 -1 0 0] is possible, but is OK only if the regressors coding for the delay are all equal

Toy example: take home. . . w F tests have to be used when - Testing for >0 and <0 effects - Testing for more than 2 levels in factorial designs - Conditions are modelled with more than one regressor w F tests can be viewed as testing for - the additional variance explained by a larger model wrt a simpler model, or - the sum of the squares of one or several combinations of the betas (here the F test b 1 – b 2 is the same as b 2 – b 1, but two tailed compared to a t-test).