Splay trees Sleator Tarjan 1983 1 Goal Support

Splay trees (Sleator, Tarjan 1983) 1

Goal Support the same operations as previous search trees. 2

Highlights • binary • simple • good amortized property • very elegant • interesting open conjectures -- further and deeper understanding of this data structure is still due 3

Main idea • Try to arrange so frequently used items are near the root • We shall assume that there is an item in every node including internal nodes. We can change this assumption so that items are at the leaves. 4

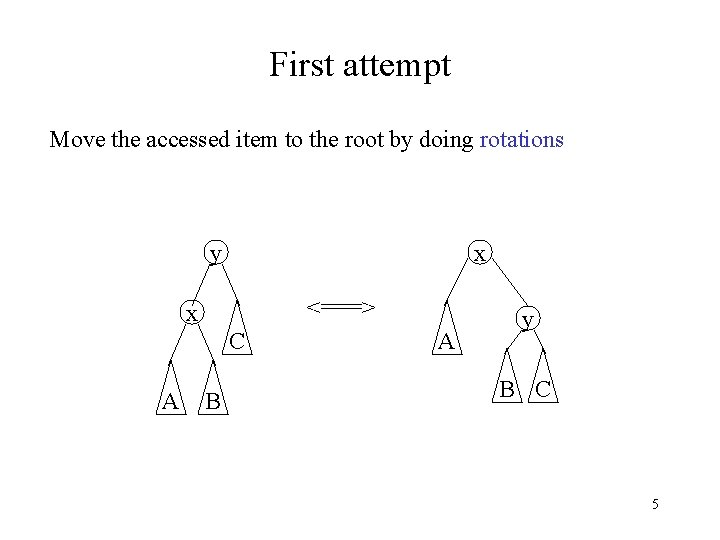
First attempt Move the accessed item to the root by doing rotations y x <===> x C A B A y B C 5

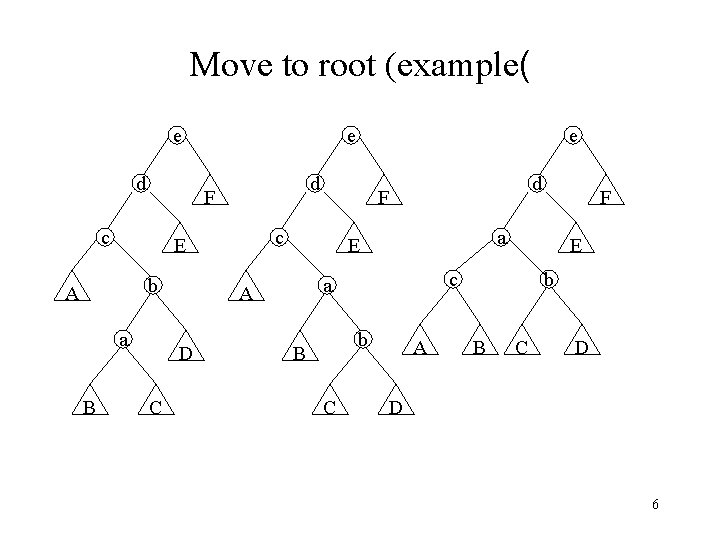
Move to root (example( e d b a C b C E c a B F a E A D d F c E A e d F c B e A b B C D D 6

Move to root (analysis( There arbitrary long access sequences such that the time per access is O(n) ! 7

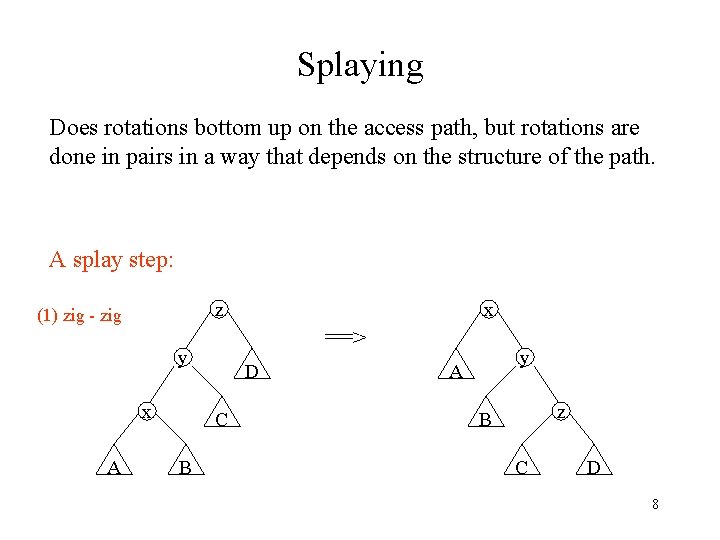
Splaying Does rotations bottom up on the access path, but rotations are done in pairs in a way that depends on the structure of the path. A splay step: z (1) zig - zig ==> y x A D C B x y A z B C D 8

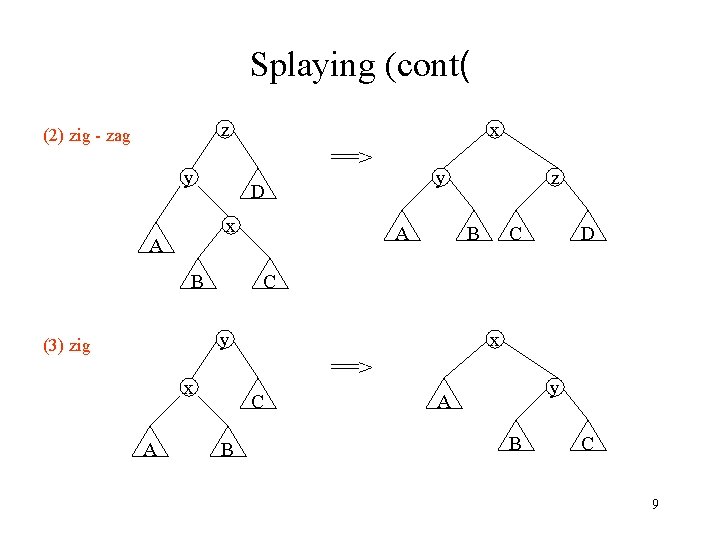
Splaying (cont( z (2) zig - zag x ==> y x A y D B A B D x ==> x A C C y (3) zig z C B y A B C 9

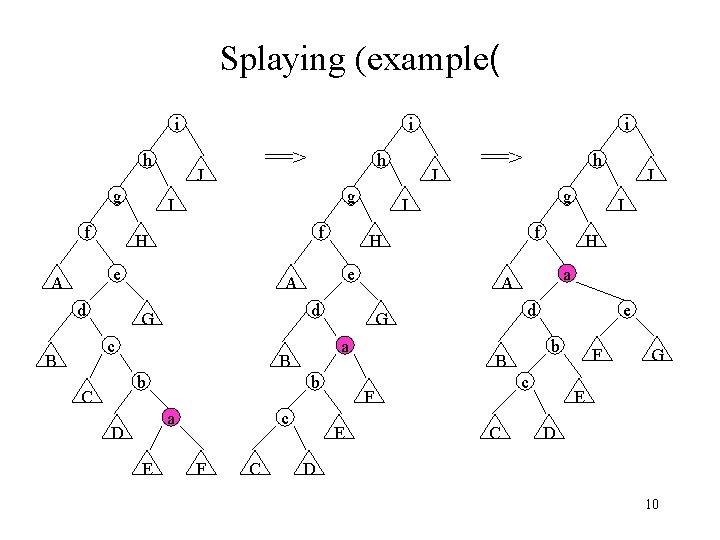
Splaying (example( i i h g f ==> J g I f H e A d b C e D E c F C E H a d e b B c F C J I f G b a g A a B h I d G J ==> H A c B h i F G E D D 10

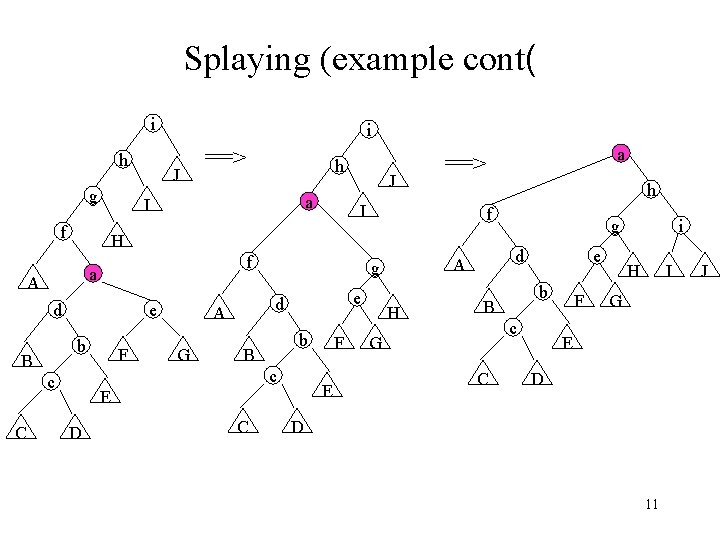
Splaying (example cont( i h g J ==> a J a ==> h I f H f a A d e b B h I f F A G e d b B E E D C F H g d A g c c C i e b B c G C F i H I G E D D 11 J

Splaying (analysis( Assume each item i has a positive weight w(i) which is arbitrary but fixed. Define the size s(x) of a node x in the tree as the sum of the weights of the items in its subtree. The rank of x: r(x) = log 2(s(x)) Measure the splay time by the number of rotations 12

Access lemma The amortized time to splay a node x in a tree with root t is at most 3(r(t) - r(x)) + 1 = O(log(s(t)/s(x))) Potential used: The sum of the ranks of the nodes. This has many consequences: 13

Balance theorem Balance Theorem: Accessing m items in an n node splay tree takes O((m+n) log n) Proof. Assign weight of 1/n to each item. The total weight is then W=1. To splay at any item takes 3 log(n) +1 amortized time the total potential drop is at most n log(n) More consequences after the proof. 14

Proof of the access lemma The amortized time to splay a node x in a tree with root t is at most 3(r(t) - r(x)) + 1 = O(log(s(t)/s(x))) proof. Consider a splay step. Let s and s’, r and r’ denote the size and the rank function just before and just after the step, respectively. We show that the amortized time of a zig step is at most 3(r’(x) - r(x)) + 1, and that the amortized time of a zig-zig or a zig-zag step is at most 3(r’(x) -r(x)) The lemma then follows by summing up the cost of all splay steps 15

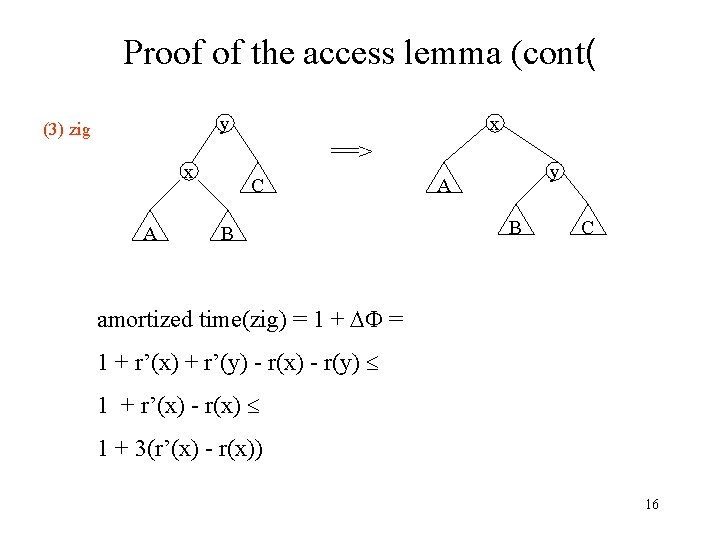
Proof of the access lemma (cont( y (3) zig ==> x A x C B y A B C amortized time(zig) = 1 + r’(x) + r’(y) - r(x) - r(y) 1 + r’(x) - r(x) 1 + 3(r’(x) - r(x)) 16

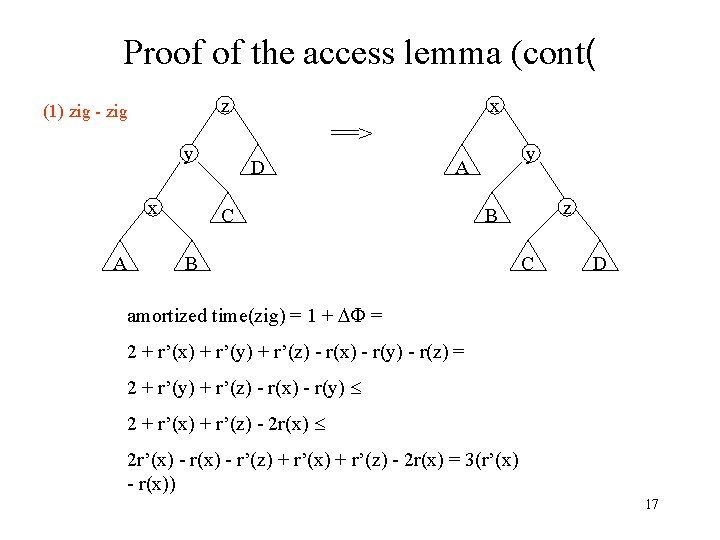
Proof of the access lemma (cont( ==> y x A x z (1) zig - zig D y A C z B B C D amortized time(zig) = 1 + = 2 + r’(x) + r’(y) + r’(z) - r(x) - r(y) - r(z) = 2 + r’(y) + r’(z) - r(x) - r(y) 2 + r’(x) + r’(z) - 2 r(x) 2 r’(x) - r’(z) + r’(x) + r’(z) - 2 r(x) = 3(r’(x) - r(x)) 17

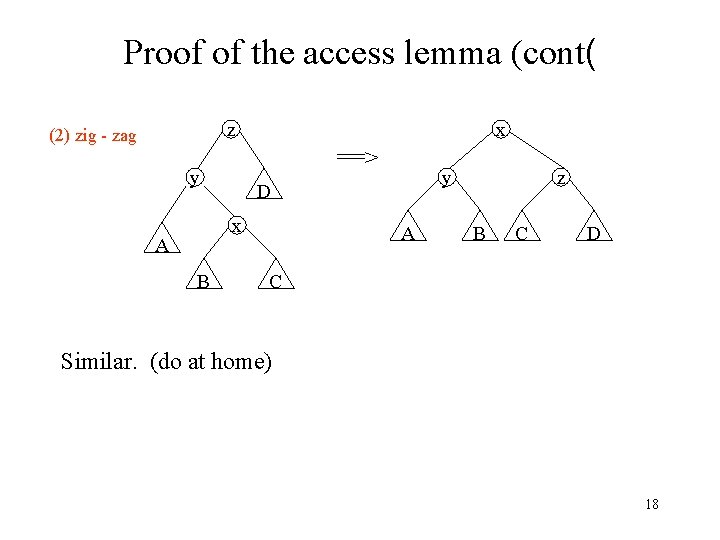
Proof of the access lemma (cont( z (2) zig - zag x ==> y x A B y D A z B C D C Similar. (do at home) 18

More consequences Suppose all items are numbered from 1 to n in symmetric order. Let the sequence of accessed items be i 1, i 2, . . , im Static finger theorem: Let f be an arbitrary fixed item, the total m access time is O(nlog(n) + m + j=1 log(|ij-f| + 1)) Splay trees support access within the vicinity of any fixed finger as good as finger search trees. 19

Static optimality theorem For any item i let q(i) be the total number of time i is accessed Static optimality theorem: If every item is accessed at least once n the total access time is O(m + q(i) log (m/q(i)) ) i=1 Optimal average access time up to a constant factor. 21

Static optimality theorem (proof( Static optimality theorem: If every item is accessed at least once n the total access time is O(m + q(i) log (m/q(i)) ) i=1 Proof. Assign weight of q(i)/m to item i. Then W=1. Amortized time to splay at i is 3 log(m/q(i)) + 1 Maximum potential drop over the sequence is n log(W)- log (q(i)/m) i=1 22

Application: Data Compression via Splay Trees Suppose we want to compress text over some alphabet Prepare a binary tree containing the items of at its leaves. To encode a symbol x: • Traverse the path from the root to x spitting 0 when you go left and 1 when you go right. • Splay at the parent of x and use the new tree to encode the next symbol 23

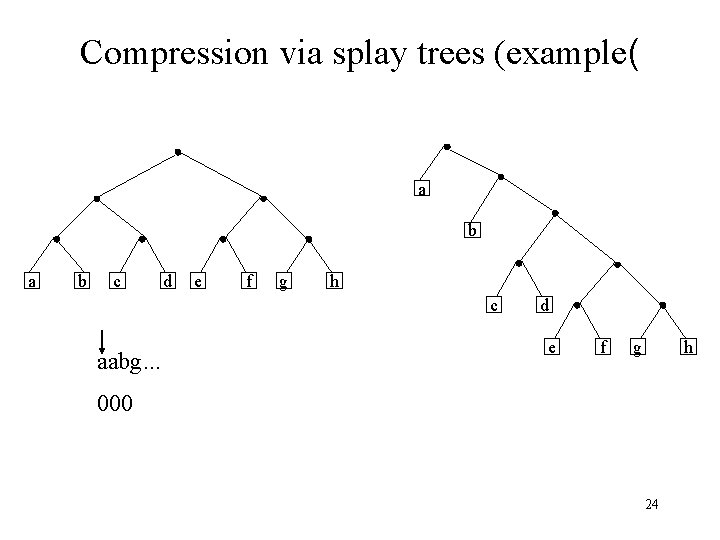
Compression via splay trees (example( a b c d e f g h c aabg. . . d e f g h 000 24

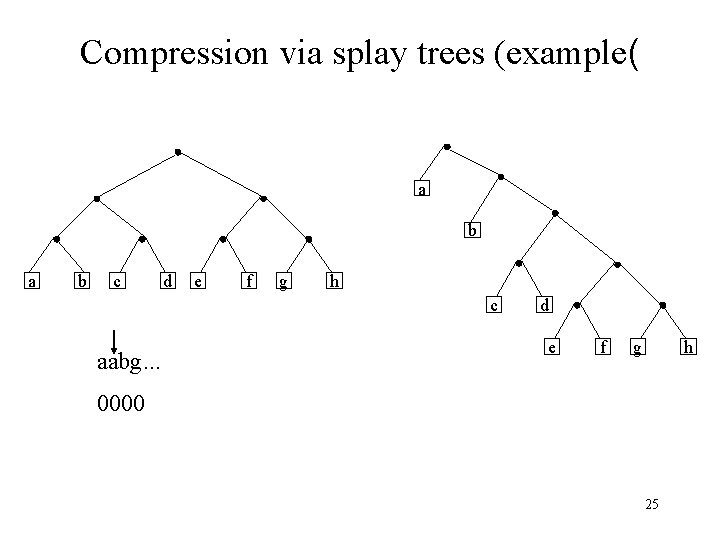
Compression via splay trees (example( a b c d e f g h c aabg. . . d e f g h 0000 25

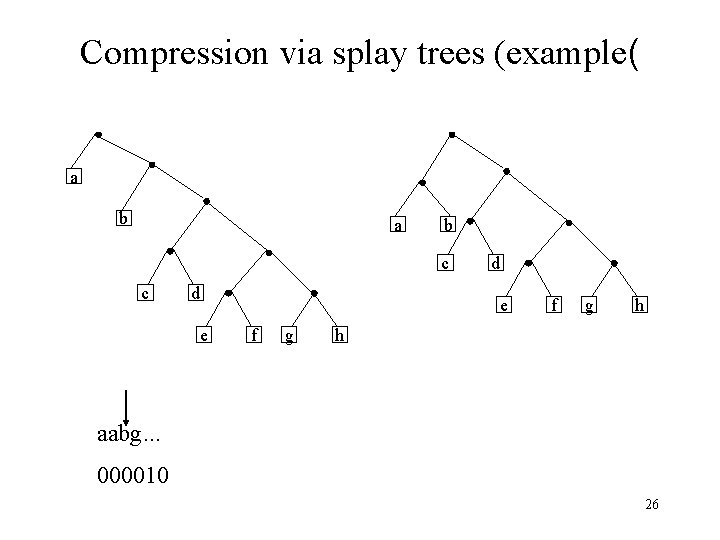
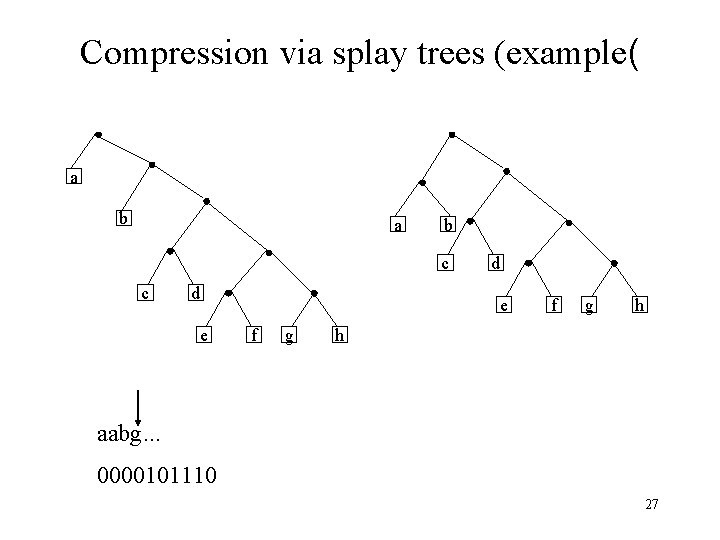
Compression via splay trees (example( a b c c d e f g h h aabg. . . 000010 26

Compression via splay trees (example( a b c c d e f g h h aabg. . . 0000101110 27

Decoding Symmetric. The decoder and the encoder must agree on the initial tree. 28

Compression via splay trees (analysis( How compact is this compression ? Suppose m is the # of characters in the original string The length of the string we produce is m + (cost of splays) by the static optimality theorem m + O(m + q(i) log (m/q(i)) ) = O(m + q(i) log (m/q(i)) ) Recall that the entropy of the sequence q(i) log (m/q(i)) is a lower bound. 29

Compression via splay trees (analysis( In particular the Huffman code of the sequence is at least q(i) log (m/q(i)) But to construct it you need to know the frequencies in advance 30

Compression via splay trees (variations( D. Jones (88) showed that this technique could be competitive with dynamic Huffman coding (Vitter 87) Used a variant of splaying called semi-splaying. 31

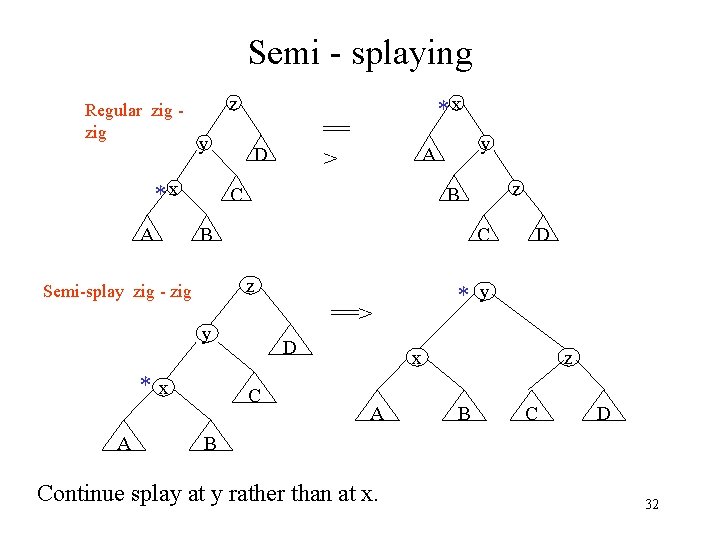
Semi - splaying Regular zig z y *x A == > D y A C C z D C D * y ==> y *x z B B Semi-splay zig - zig A *x x A z B C D B Continue splay at y rather than at x. 32

Update operations on splay trees Catenate(T 1, T 2): Splay T 1 at its largest item, say i. Attach T 2 as the right child of the root. i T 1 T 2 T 1 i T 2 T 1 T 2 s(T 1) + s(T 2) Amortize time: 3(log(s(T 1)/s(i)) + 1 + log( ) s(T 1) ≤ 3 log(W/w(i)) + O(1) 38

Update operations on splay trees (cont( split(i, T): Assume i T Splay at i. Return the two trees formed by cutting off the right son of i i i T T 1 T 2 Amortized time = 3 log(W/w(i)) + O(1) 39

Update operations on splay trees (cont( split(i, T): What if i T ? Splay at the successor or predecessor of i (i- or i+). Return the two trees formed by cutting off the right son of i or the left son of i ii. T T 1 T 2 Amortized time = 3 log(W/min{w(i-), w(i+)}) + O(1) 40

Update operations on splay trees (cont( insert(i, T): Perform split(i, T) ==> T 1, T 2 Return the tree i T 1 T 2 W-w(i) ) + log(W/w(i)) + O(1) Amortize time: 3 log( min{w(i-), w(i+)} 41

Update operations on splay trees (cont( delete(i, T): Splay at i and then return the catenation of the left and right subtrees i + T 1 T 2 Amortize time: 3 log(W/w(i)) + 3 log( W-w(i) w(i-) ) + O(1) 42

Open problems Self adjusting form of a, b tree ? 43

Open problems Dynamic optimality conjecture: Consider any sequence of successful accesses on an n-node search tree. Let A be any algorithm that carries out each access by traversing the path from the root to the node containing the accessed item, at the cost of one plus the depth of the node containing the item, and that between accesses perform rotations anywhere in the tree, at a cost of one per rotation. Then the total time to perform all these accesses by splaying is no more than O(n) plus a constant time the cost of algorithm A. 44