Spin Precession Animation DEMO The Nucleus would continue

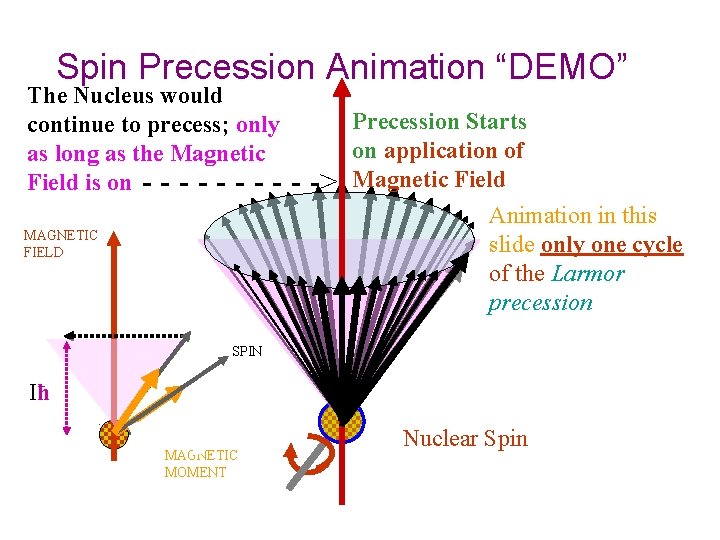
Spin Precession Animation “DEMO” The Nucleus would continue to precess; only as long as the Magnetic Field is on - - - - -> Precession Starts on application of Magnetic Field Animation in this slide only one cycle of the Larmor precession MAGNETIC FIELD μXH SPIN Iħ MAGNETIC MOMENT Nuclear Spin

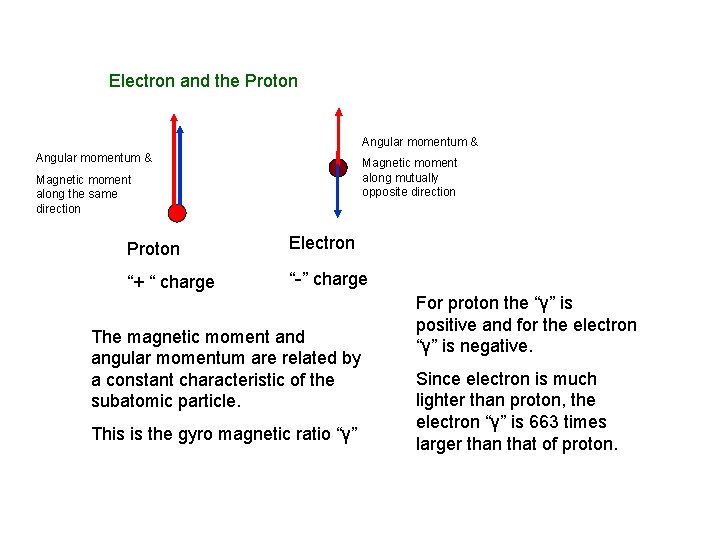
Electron and the Proton Angular momentum & Magnetic moment along mutually opposite direction Magnetic moment along the same direction Proton Electron “+ “ charge “-” charge The magnetic moment and angular momentum are related by a constant characteristic of the subatomic particle. This is the gyro magnetic ratio “γ” For proton the “γ” is positive and for the electron “γ” is negative. Since electron is much lighter than proton, the electron “γ” is 663 times larger than that of proton.

A Thumb rule to work out Electron Spin Resonance Frequency [and the corresponding Proton NMR frequency] is as follows: since hν=gβH is the relation governing resonance condition, by knowing the relevant constants from available data tables, it should be verified that the following equation closely approximates the resonance frequency-field criterion for ESR. 1 Gauss = 2. 8 MHz for a free electron spin with g=2 For proton NMR 1 Gauss = 4. 2 KHz Therefore if one can detect the oscillator levels using an oscillatordetector, and , if the frequencies of the oscillations are in the range of 8 -32 MHz, then using the above equation the corresponding 1. 9 resonance field can be calculated. 2. 9 – 11. 5 Gauss for ESR. Further a simple Helmholtz coil can be designed to obtain these Magnetic Field Strengths by providing a suitably designed current sources which may be available even commercially. – 7. 6 K Gauss Then a Block Diagram of the type shown in the next slide can be appropriate for constructing and assembling a esr detection system. for PMR

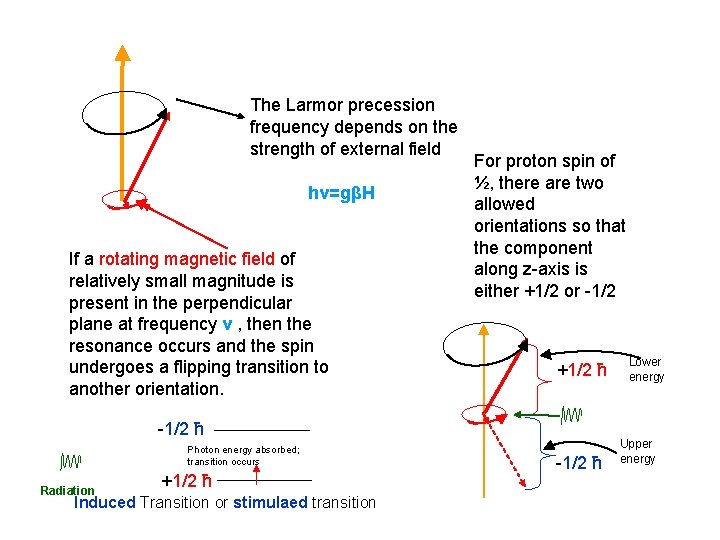
The Larmor precession frequency depends on the strength of external field hν=gβH If a rotating magnetic field of relatively small magnitude is present in the perpendicular plane at frequency ν , then the resonance occurs and the spin undergoes a flipping transition to another orientation. For proton spin of ½, there are two allowed orientations so that the component along z-axis is either +1/2 or -1/2 +1/2 ħ -1/2 ħ Photon energy absorbed; transition occurs Radiation +1/2 ħ Induced Transition or stimulaed transition -1/2 ħ Lower energy Upper energy

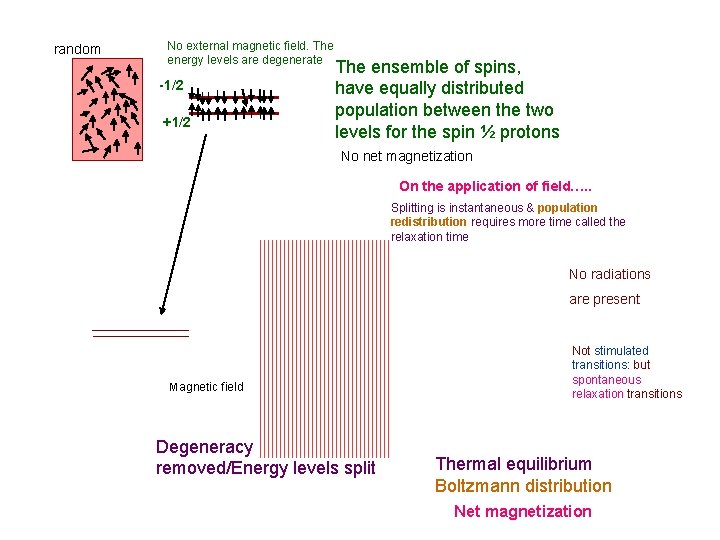
random No external magnetic field. The energy levels are degenerate -1/2 +1/2 The ensemble of spins, have equally distributed population between the two levels for the spin ½ protons No net magnetization On the application of field…. . Splitting is instantaneous & population redistribution requires more time called the relaxation time -1/2 No radiations are present -1/2 +1/2 Not stimulated transitions: but spontaneous relaxation transitions Magnetic field +1/2 Degeneracy removed/Energy levels split Thermal equilibrium Boltzmann distribution Net magnetization